Volume is the amount of space inside the boundary of a solid (i.e. 3-dimensional) object.

By this stage you will be familiar with calculating the volumes of most standard shapes, but the key volume formulas you should know are given below as a reminder:

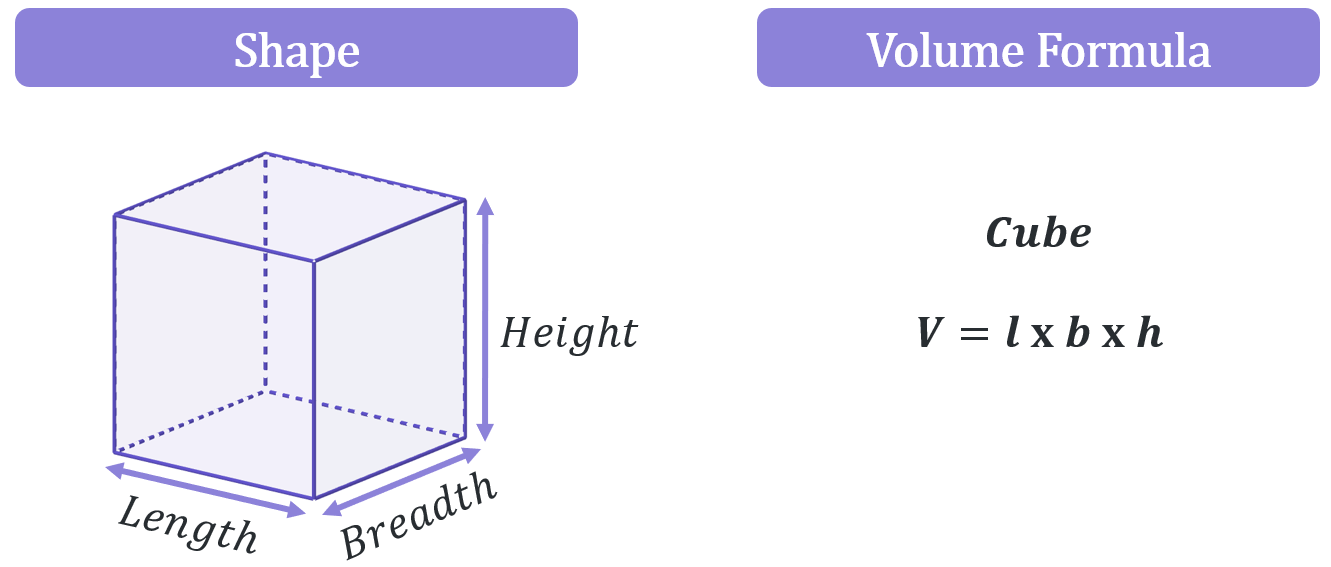
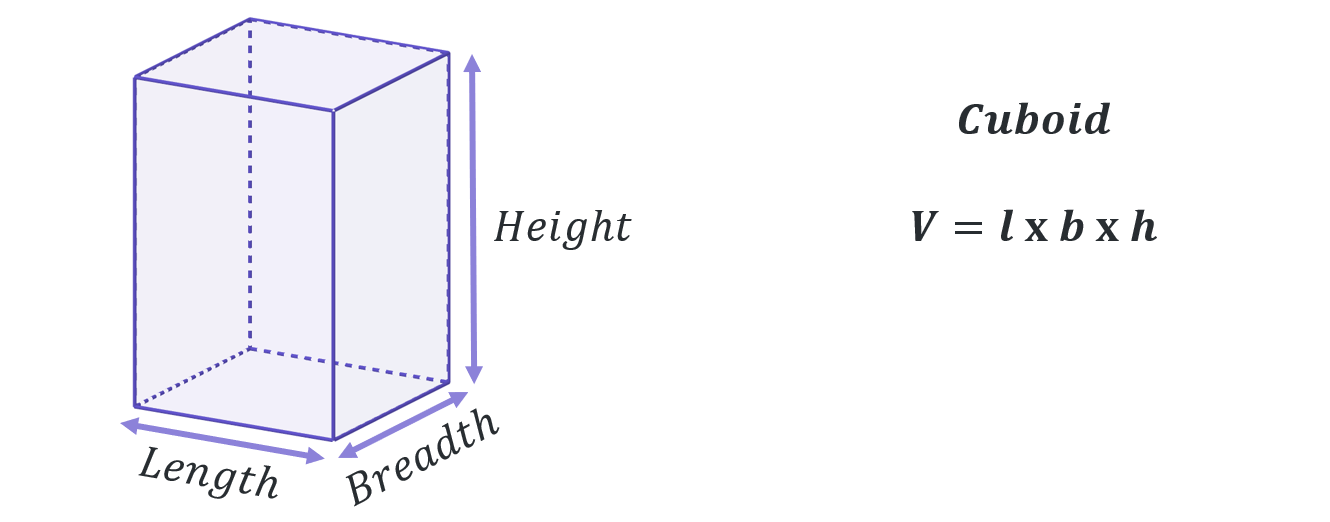
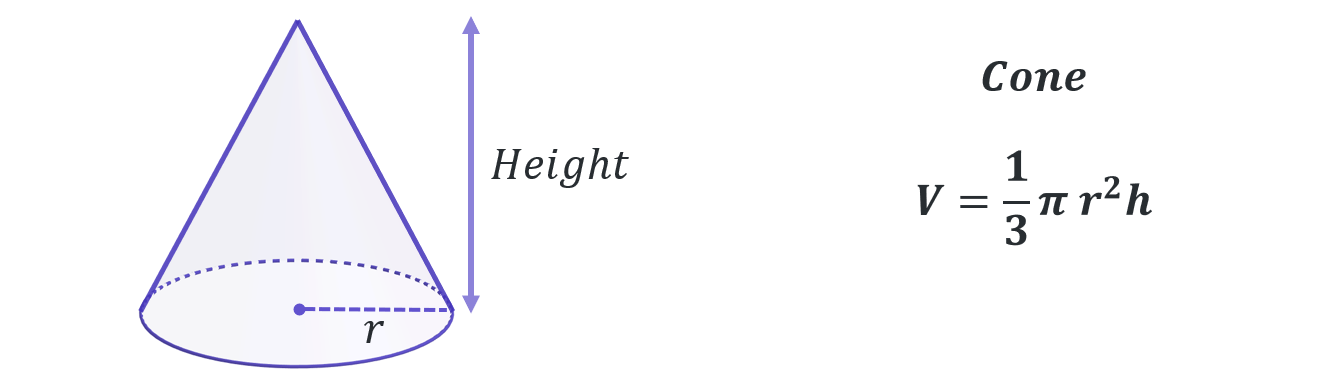
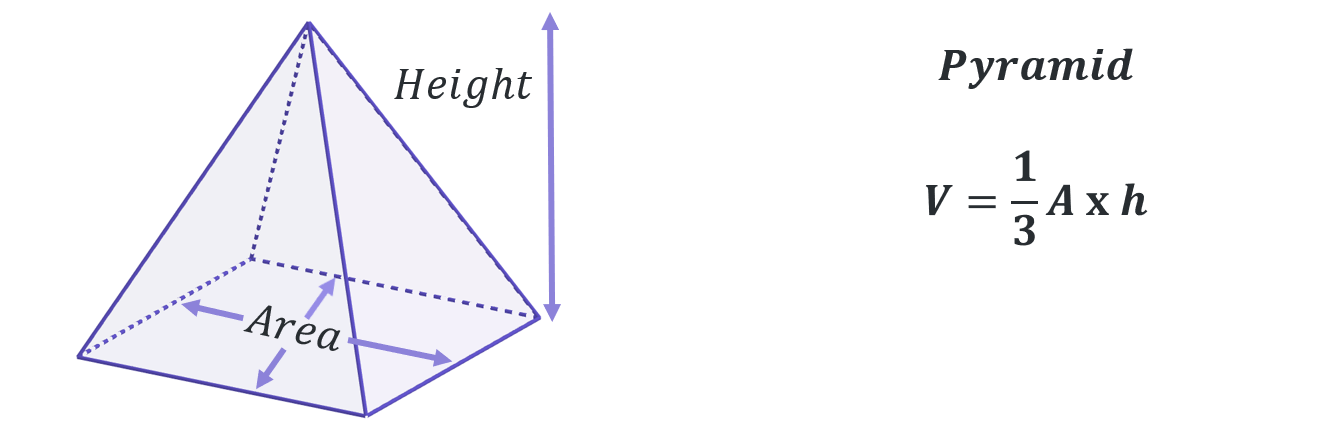
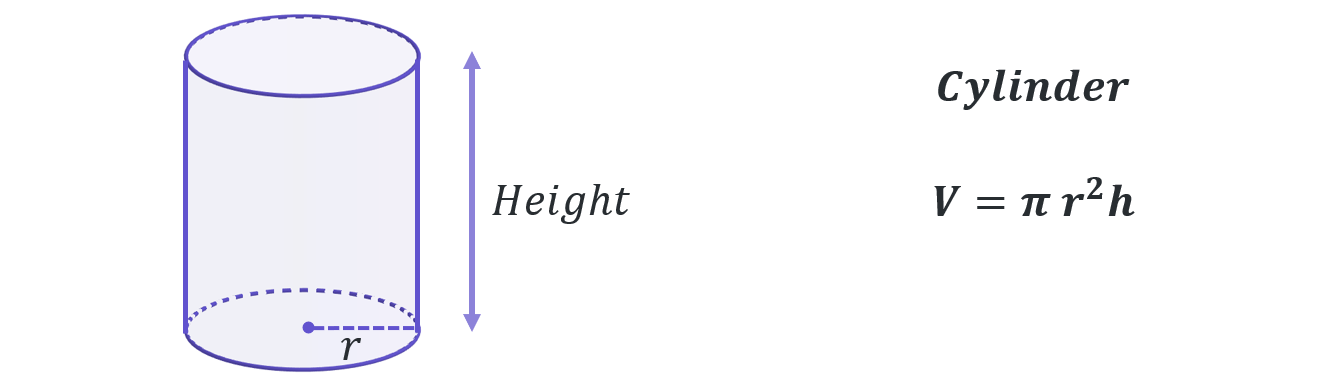
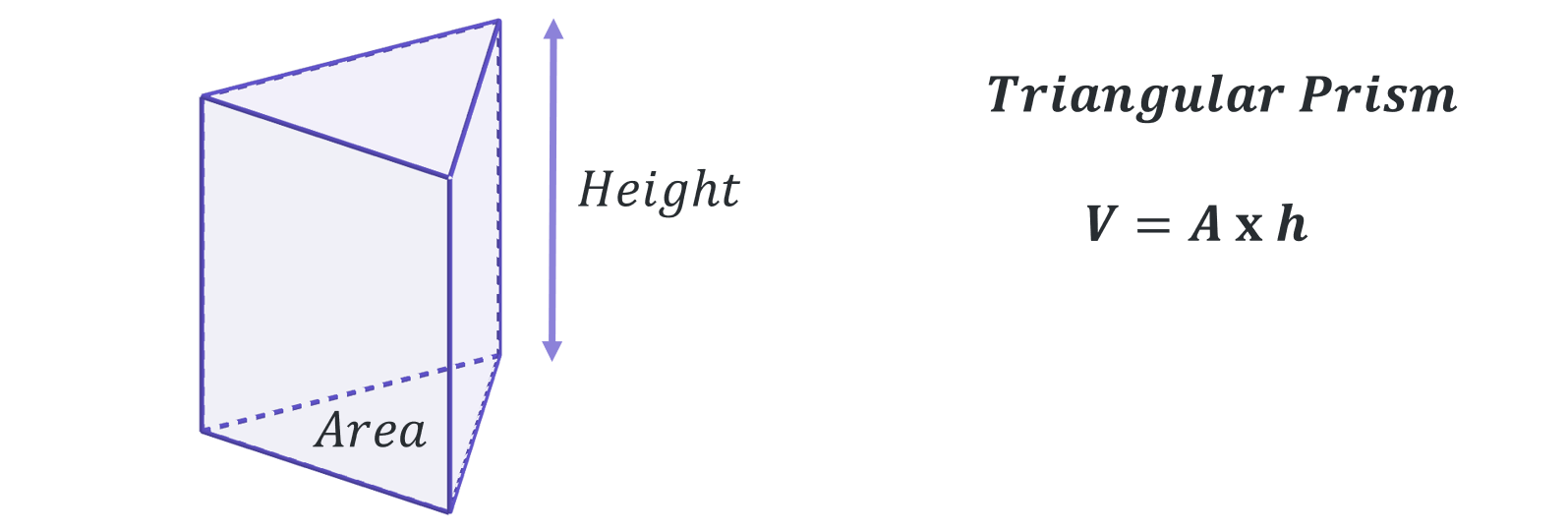
A composite solid is a compound shape in 3-dimensions. It is a shape that can be split up into several simpler, standard geometric volumes such as cubes, cuboids, cylinders, prisms, cones etc…

Finding the volume of a composite solid follows the same principal we learned when working with composite areas in the previous module:

Let’s work through a few examples:

A birdwatcher builds a birdhouse to attract birds to his garden:

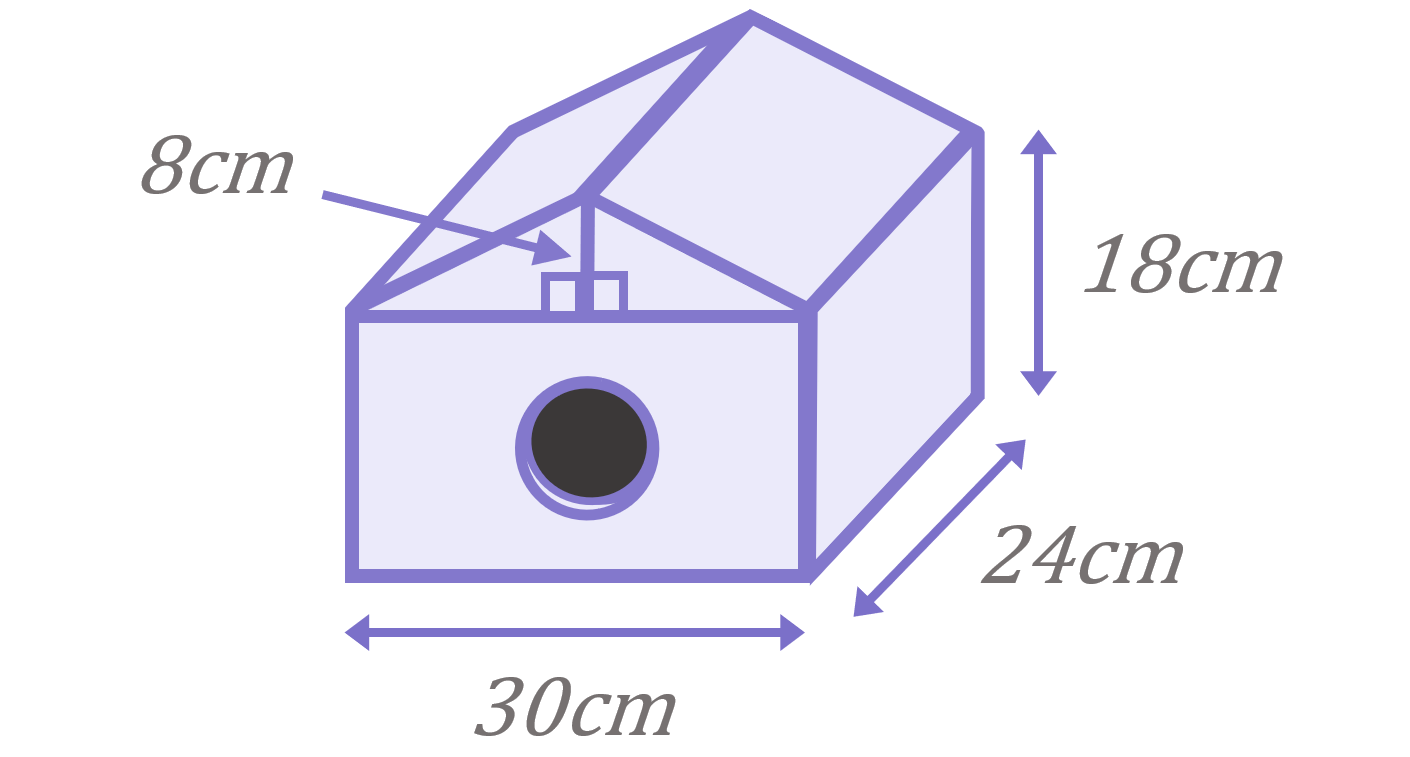
Calculate the volume of his birdhouse.

We can split this composite solid into a cuboid and a triangular prism, and work out the volume of each to get to the total volume:

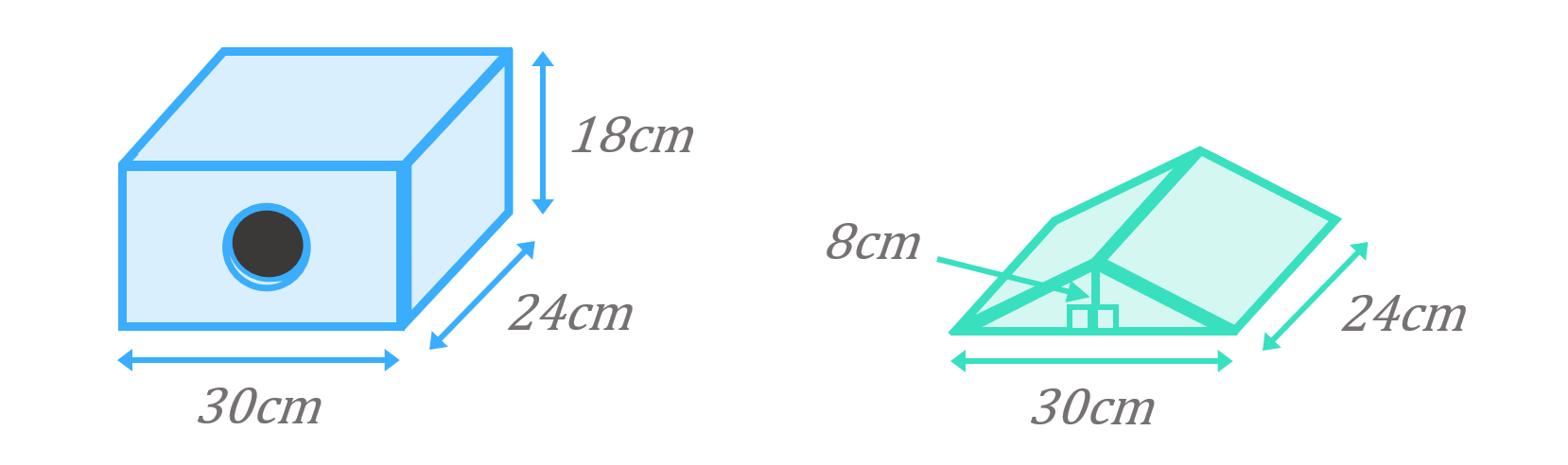
\begin{aligned}\text{Volume of cuboid}&=l\times b\times h \\[12pt]\text{Volume of cuboid}&=30\times 24\times 18 \\[12pt]\text{Volume of cuboid}&=12,960cm^{3}\end{aligned}

\begin{aligned}\text{Volume of triangular prism}&=A\times h \\[12pt]\text{Volume of triangular prism}&=\left(\frac{1}{2}(30)(8)\right)\times 24 \\[16pt]\text{Volume of triangular prism}&=120\times 24 \\[12pt]\text{Volume of triangular prism}&=2,880cm^{3}\end{aligned}

Now we can easily find the total volume of the birdhouse by adding the two composite volumes together:

\begin{aligned}\text{Volume of birdhouse}&=12,960+2,880 \\[12pt]\text{Volume of birdhouse}&=15,840cm^{3}\end{aligned}

A water tower has the dimensions shown. Calculate its volume.

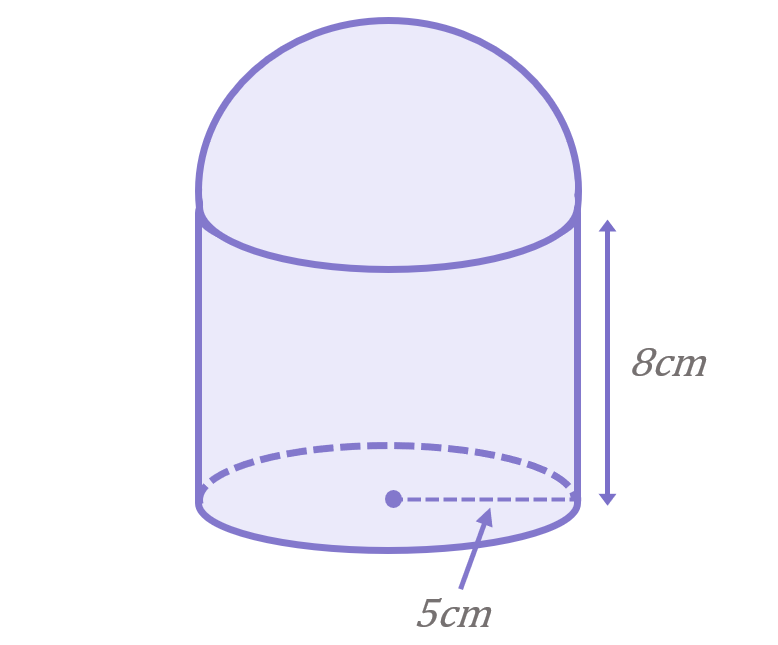
We can split this solid into a cylinder and a hemisphere, and work out the volume of each to get to the total volume:

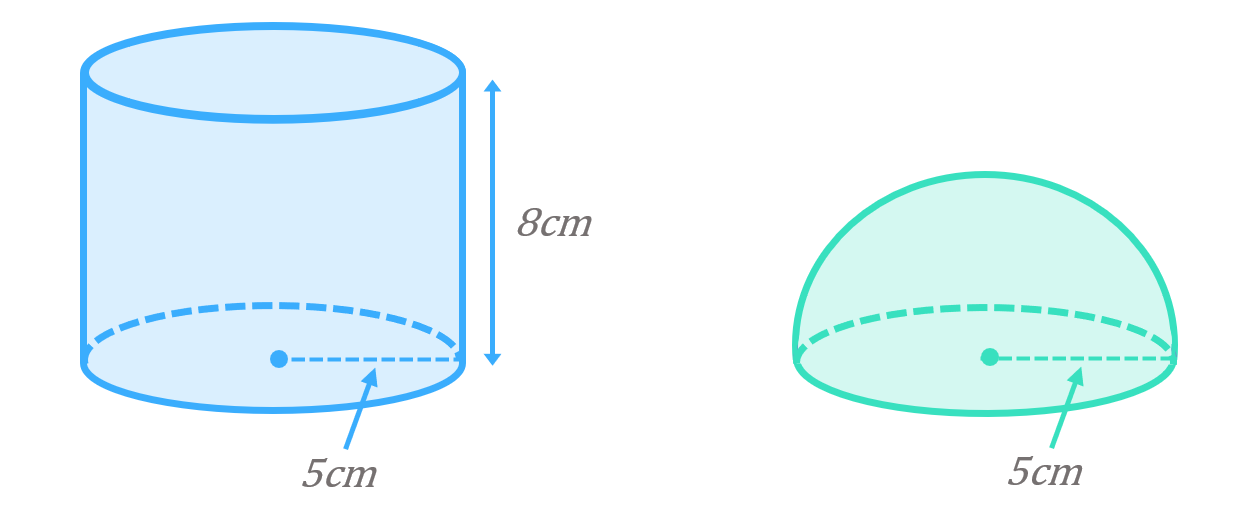
\begin{aligned}\text{Volume of cylinder}&=\pi r^{2}h \\[12pt]\text{Volume of cylinder}&=\pi(5)^{2}(8) \\[12pt]\text{Volume of cylinder}&=628.3m^{3}\end{aligned}

\begin{aligned}\text{Volume of hemisphere}&=\frac{\frac{4}{3}\pi r^{3}}{2}\end{aligned}

(Note this is just the formula for the volume of a sphere divided by two, since a hemisphere is literally half of a sphere)

\begin{aligned}\text{Volume of hemisphere}&=\frac{\frac{4}{3}\pi (5)^{3}}{2} \\[12pt]\text{Volume of hemisphere}&=\frac{523.6}{2} \\[12pt]\text{Volume of hemisphere}&=261.8m^{3}\end{aligned}

Now we can easily find the total volume of the water tower by adding the two composite volumes together:

\begin{aligned}\text{Volume of water tower}&=628.3+261.8 \\[12pt]\text{Volume of water tower}&=890.1m^{3}\end{aligned}

A cube has a conic section cut out of it as shown. What is the volume of the solid this creates?

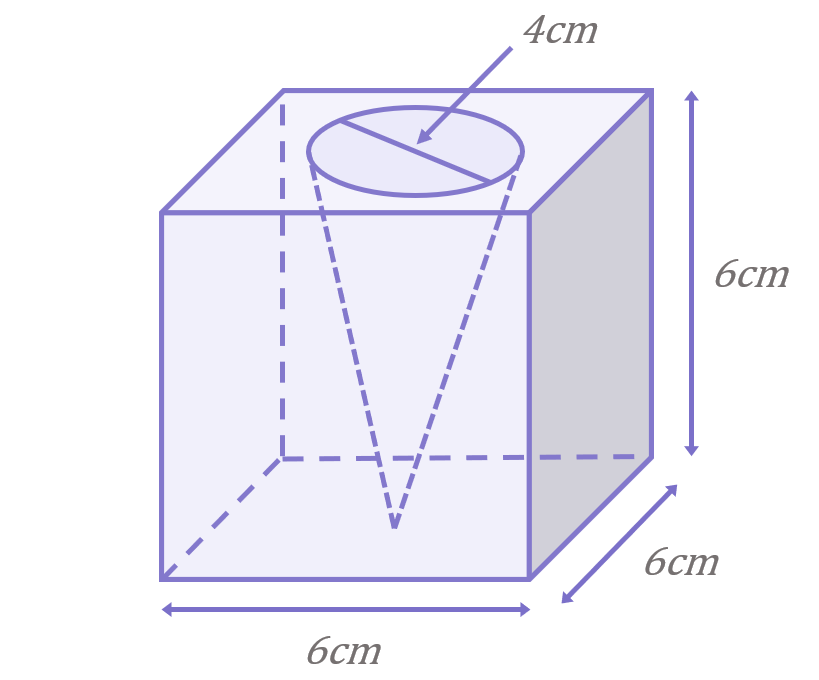
If we work out the volume of the full cube and then subtract the volume of the cone, we will be left with the volume of the remaining solid.

The cone has a diameter of 4cm, so its radius is 2cm. The cone is as deep as the height of the cube, so it also has a height of 6cm:

\begin{aligned}\text{Volume of cube}&=l\times b\times h \\[12pt]\text{Volume of cube}&=6\times 6\times 6 \\[12pt]\text{Volume of cube}&=216cm^{3}\end{aligned}

\begin{aligned}\text{Volume of cone}&=\frac{1}{3}\pi r^{2}h \\[12pt]\text{Volume of cone}&=\frac{1}{3}\pi (2)^{2}(6) \\[12pt]\text{Volume of cone}&=25.1cm^{3}\end{aligned}

Now we can easily find the total volume of the solid by subtracting the volume of the cone from the volume of the cube:

\begin{aligned}\text{Volume of solid}&=216-25.1 \\[12pt]\text{Volume of solid}&=190.9cm^{3}\end{aligned}