What are Vectors?
Suppose you are an American tourist in Edinburgh and you want to travel to St Andrews as part of your trip. You rent a car and ask an Edinburgh local how to drive to St Andrews.
The first local you ask tells you “St Andrews is a 52-mile drive from Edinburgh”. That’s good to know, but that’s not really enough information is it? It’s one thing to know the distance of St Andrews from Edinburgh, but which direction should you be driving in!?
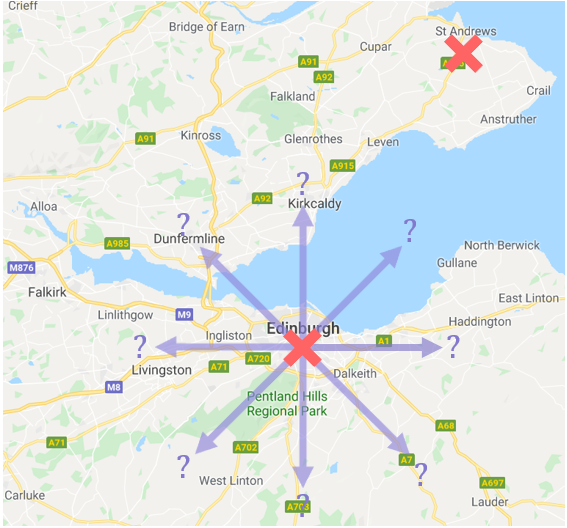
You ask a second local the same question and they tell you “St Andrews is a 52-mile drive in a North Easterly direction from Edinburgh”. That’s a bit more helpful isn’t it – now you know the exact distance and direction you need to drive in to get to St Andrews:
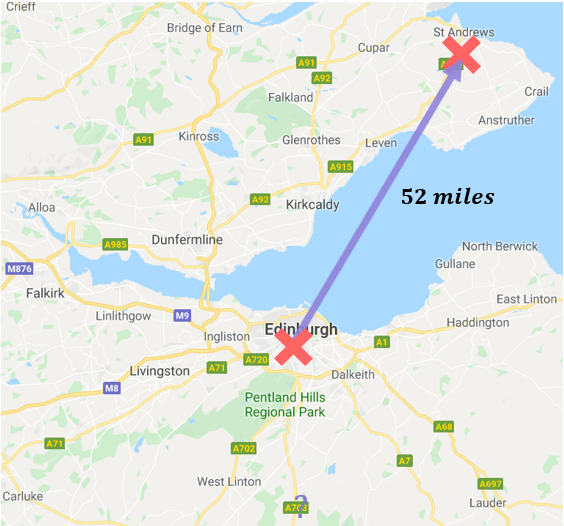
(For simplicity, we’re ignoring the fact that following this route would mean driving through the water!)
This combination of distance and direction is called displacement, which is one example of a vector:
A vector is a quantity that has both size (often called “magnitude”) and direction.
Examples of vectors include displacement and force. If you think about it, neither of these quantities make any sense without both a magnitude and direction component:
Displacement – Take our example of driving from Edinburgh to St Andrews. It wasn’t enough to know that St Andrews was 52 miles away (magnitude) or that it was in a North Easterly direction, we had to know both magnitude and direction to get there.
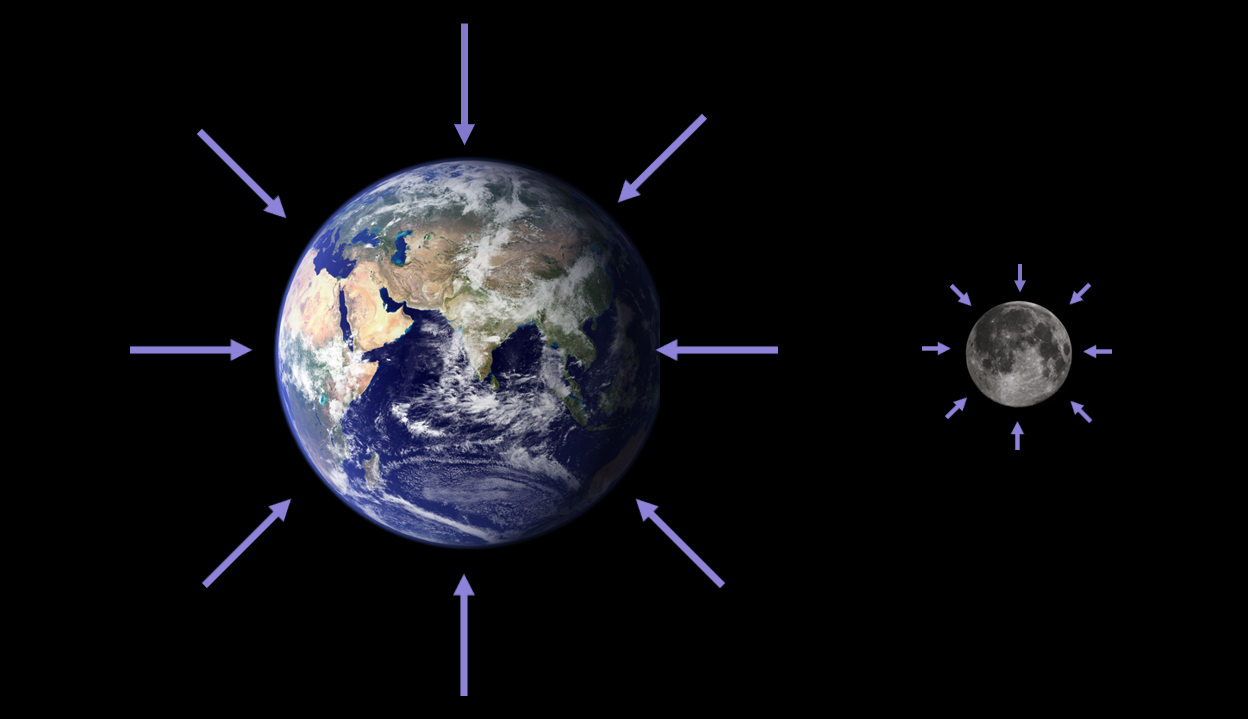
Force – Take the example of gravity. Even if you don’t study physics, I am sure you know that gravity is the force that pulls us towards the centre of the Earth (i.e. its direction) and stops us all floating out into space. The strength of gravity (i.e. its magnitude) is different on other celestial bodies – for example, gravity is far weaker on the Moon than it is here on Earth. Therefore, to understand the force of gravity fully, it’s important to know both its magnitude and direction.
Other quantities don’t require a direction component – these are scalars:
A scalar is a quantity that is fully described by its size (i.e. magnitude) only. It is described by a single number.
Some examples of scalar quantities include volume, temperature and time. It wouldn’t make any sense to attach a direction to any of these quantities would it? A box can’t have a volume in a North Easterly direction can it? It just has a volume. Water doesn’t boil at 100^\circ C South does it? It just boils at 100^\circ C. A game of football doesn’t last 90 minutes West does it? It just lasts 90 minutes. I think you get the idea!
Column Vector Notation
Now that you know what a vector is, it’s important to understand how to work with them in a mathematical context.
A vector connecting point A to point B is shown on the diagram below:
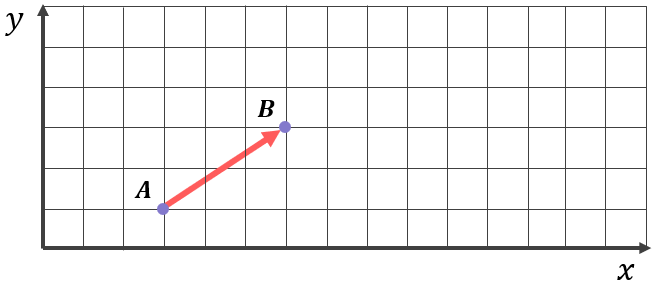
In vector notation, this vector would be labelled \overrightarrow{AB} – this is the notation for a vector connecting point A to point B.
Notice the specific direction of the vector (as indicated by the direction of the arrow) is from point A to point B and not the other way around. If the arrow was facing the other way, going from point B to point A:
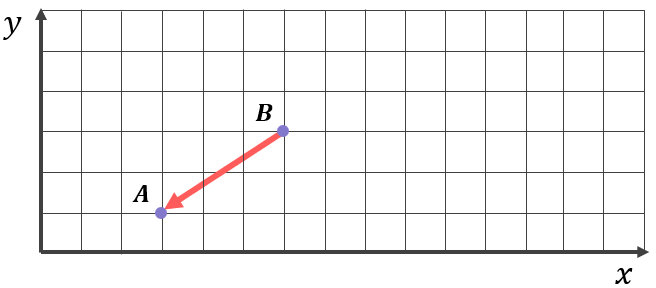
This vector would instead be labelled \overrightarrow{BA}.
The labelling of vectors is very important. The vector \boldsymbol{\overrightarrow{AB}} indicates a vector connecting point A to point B, whereas the vector \boldsymbol{\overrightarrow{BA}} indicates a vector connecting point B to point A. The vectors \boldsymbol{\overrightarrow{AB}} and \boldsymbol{\overrightarrow{BA}} therefore have the same length but point in opposite directions.
Vectors represented in diagrams like those above are sometimes called directed line segments.
The arrow is often called the “head” of the vector, with the other end being the “tail”.
Any vector such as \overrightarrow{AB} can be broken down into simple x and y components. Looking at the grid, it is clear that to get from point A to point B, we have to move 3 units in the positive x direction and 2 units in the positive y direction:
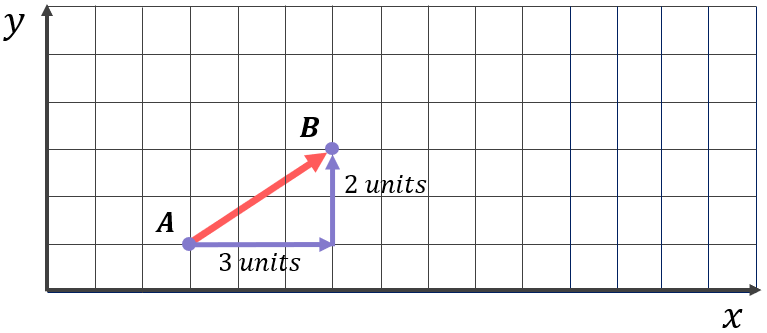
This is summarised by expressing the vector \overrightarrow{AB} as a column vector:
\overrightarrow{AB}=\begin{pmatrix}3 \\ 2\end{pmatrix}
When expressed as a column vector (which is sometimes called “component form”) the top number indicates the \boldsymbol{x}-component (i.e. the horizontal movement) and the bottom number indicates the \boldsymbol{y}-component (i.e. the vertical movement) of the vector.
For the \boldsymbol{x}-component:
Positive number = move to the right
Negative number = move to the left
For the \boldsymbol{y}-component:
Positive number = move upwards
Negative number = move downwards
Think of a column vector such as \boldsymbol{\overrightarrow{AB}=\begin{pmatrix}3 \\ 2\end{pmatrix}} as the “instructions” to move from point A to point B.
Comparing the vectors \overrightarrow{AB} and \overrightarrow{BA} next to each other should make it clear how this direction convention works:
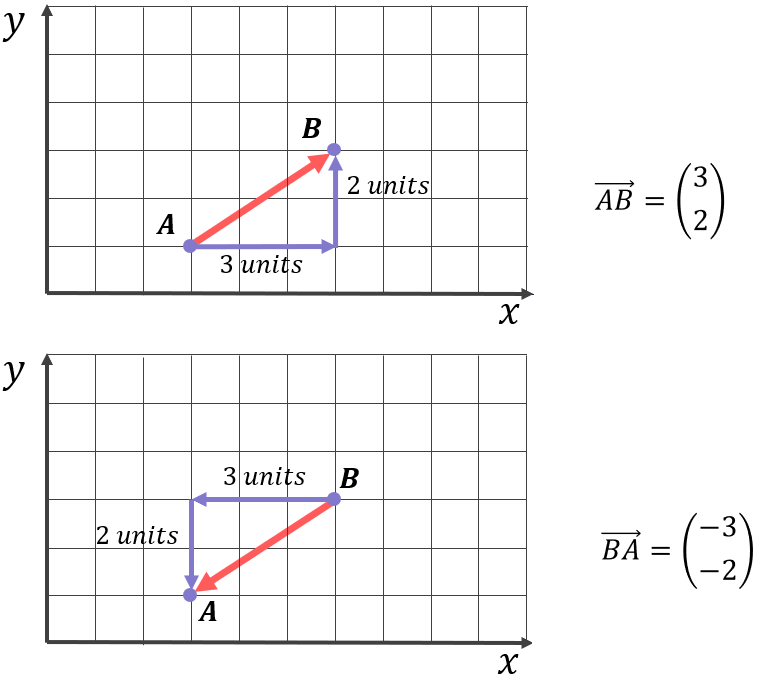
Further:
The length of a vector indicates its size (i.e. its magnitude).
For example:
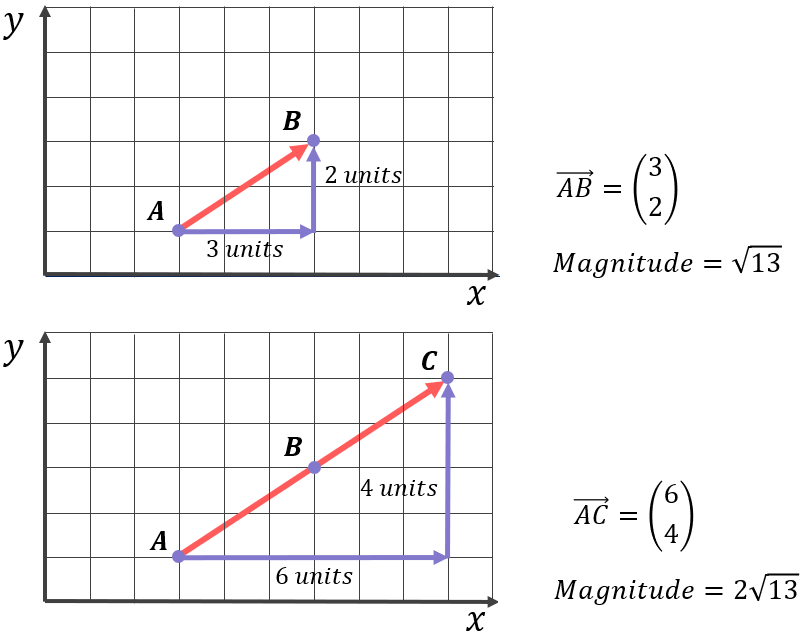
The vector \overrightarrow{AC} has exactly the same direction as \overrightarrow{AB} (the arrows are pointing the same way), but \overrightarrow{AC} is twice as long as \overrightarrow{AB}, so its magnitude (i.e. size) is twice as big. (Don’t worry if you do not yet know how to calculate the magnitude of a vector, we discuss this in a later topic)
Finally, have a look at the 5 vectors in the diagram below:
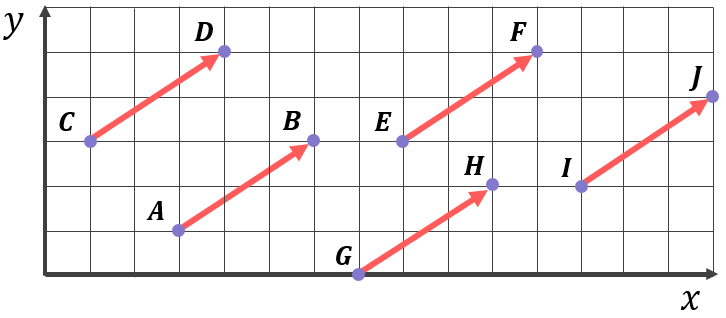
These 5 vectors are equal vectors because, even though these vectors lie in different physical positions on the grid, they all have the same components:
\overrightarrow{AB}=\begin{pmatrix}3 \\ 2\end{pmatrix} \\[12pt]\overrightarrow{CD}=\begin{pmatrix}3 \\ 2\end{pmatrix} \\[12pt]\overrightarrow{EF}=\begin{pmatrix}3 \\ 2\end{pmatrix} \\[12pt]\overrightarrow{GH}=\begin{pmatrix}3 \\ 2\end{pmatrix} \\[12pt]\overrightarrow{IJ}=\begin{pmatrix}3 \\ 2\end{pmatrix}
In other words, the instructions to get from the tail to the head of any of these vectors is the same: move 3 units in the positive x direction and 2 units in the positive y direction.
When two vectors have the same components, they are equal to each other. Equal vectors have the same magnitude and direction.
(Note that the 5 vectors in the diagram above are all the same length and pointing in the same direction. They therefore must be equal vectors)
Although the 5 vectors in the above diagram lie in different physical positions on the grid, they are nevertheless equal because they have the same length and are in the same direction. To discuss the actual position of vectors on a grid or coordinate system, you need position vectors which are a tool we discuss in a later topic.
Key Outcomes
A scalar is a quantity that is fully described by its size (often called “magnitude”) only. It is described by a single number.
A vector is a quantity that has both magnitude and direction.
The labelling of vectors is very important. The vector \overrightarrow{AB} indicates a vector connecting point A to point B, whereas the vector \overrightarrow{BA} indicates a vector connecting point B to point A. The vectors \overrightarrow{AB} and \overrightarrow{BA} therefore have the same length but opposite directions.
Vectors represented in diagrams are sometimes called directed line segments.
The arrow is often called the “head” of the vector, with the other end being the “tail”.
When expressed as a column vector (which is sometimes called “component form”) the top number indicates the x-component (i.e. the horizontal movement) and the bottom number indicates the y-component (i.e. the vertical movement) of the vector.
For the x-component:
Positive number = move to the right
Negative number = move to the left
For the y-component:
Positive number = move upwards
Negative number = move downwards
Think of a column vector, such as \overrightarrow{AB}=\begin{pmatrix}3 \\ 2\end{pmatrix}, as the instructions to move from point A to point B.
The length of a vector indicates its size (i.e. its magnitude).
When two vectors have the same components, they are equal to each other. Equal vectors have the same magnitude and direction.