Turning Point
At the National 5 level there are two methods you should be aware of for determining the turning point of a quadratic equation: the mid-point of roots method and Completing the Square. We discuss each method in turn below:
Mid-point of roots method
Recall that all quadratics are symmetric curves and their line of symmetry always runs through their turning point. The lines of symmetry of the quadratics below have been shown as dotted lines:
In certain cases, we can use this symmetry to locate a quadratic’s turning point.
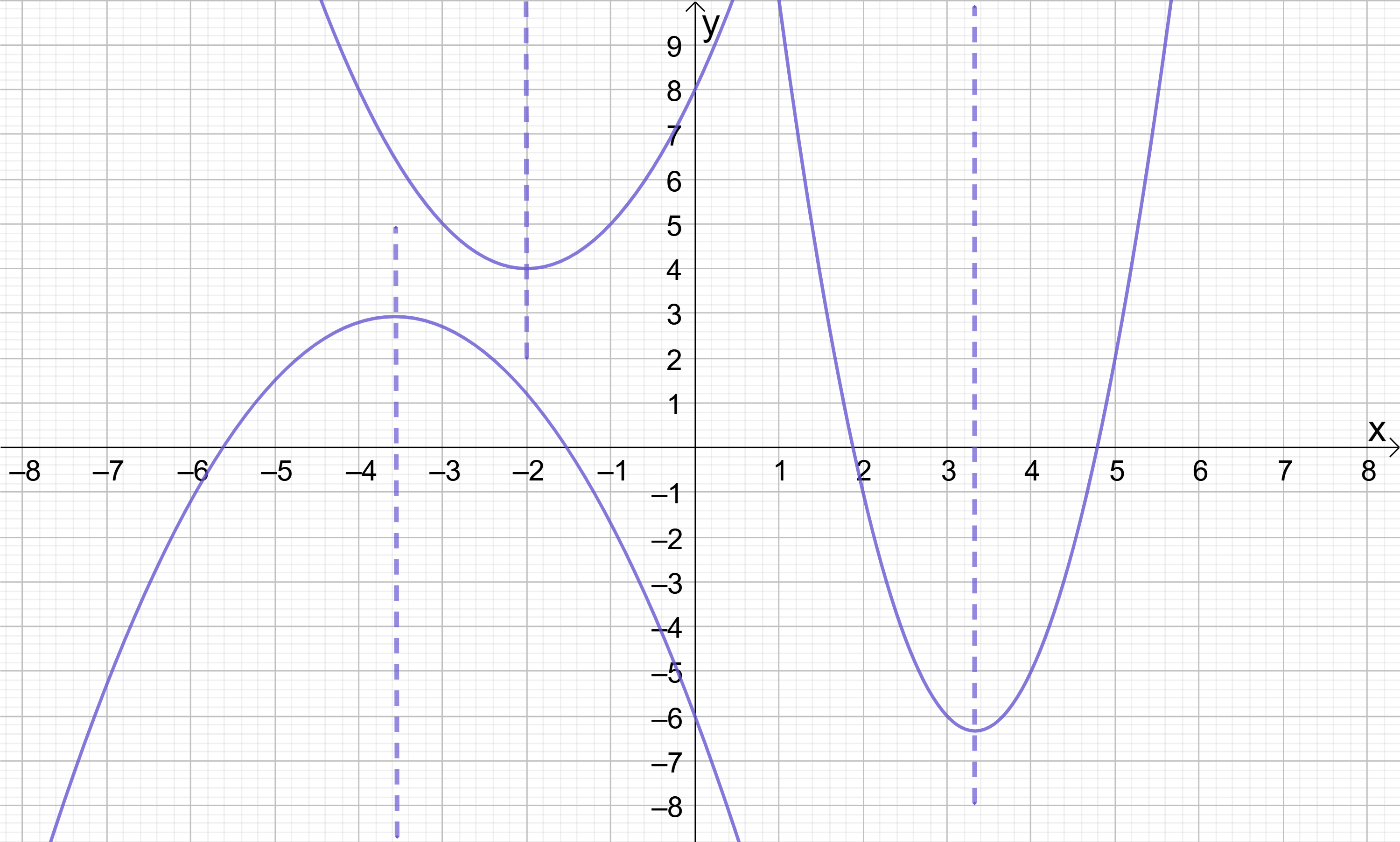
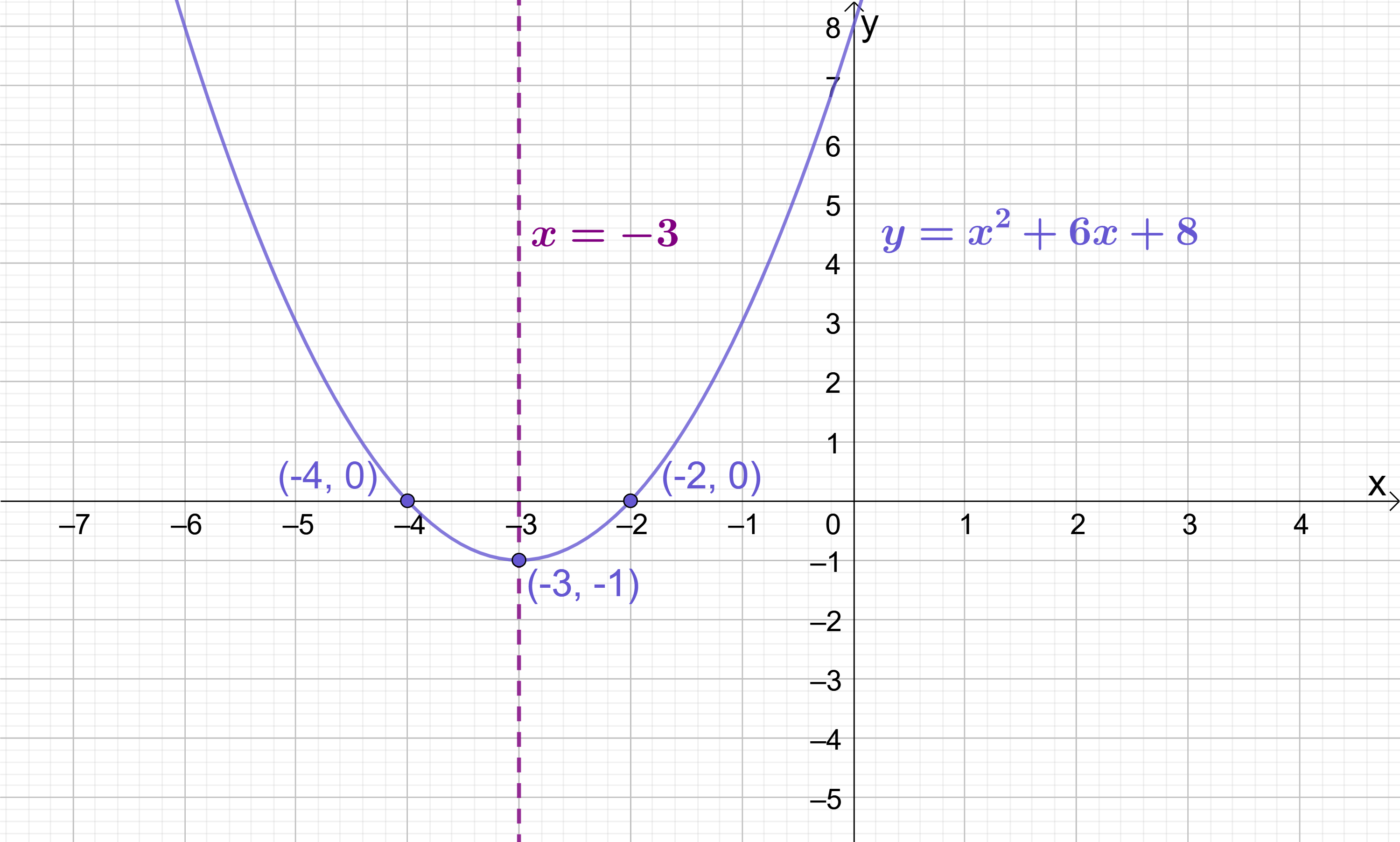
Take the example of y=x^{2}+6x+8 shown below:
For this quadratic the line of symmetry is the vertical line passing through the x-axis at (-3, 0), so its equation is simply x=-3. But since the line of symmetry also passes through the turning point, then the x-coordinate of the turning point must also be -3. We don’t yet know the y-coordinate of the turning point, so this is shown as “?”.
Now normally the line of symmetry wouldn’t be provided, so you’d need to figure out where this was yourself, but this is easy to do if you know the roots of the quadratic.
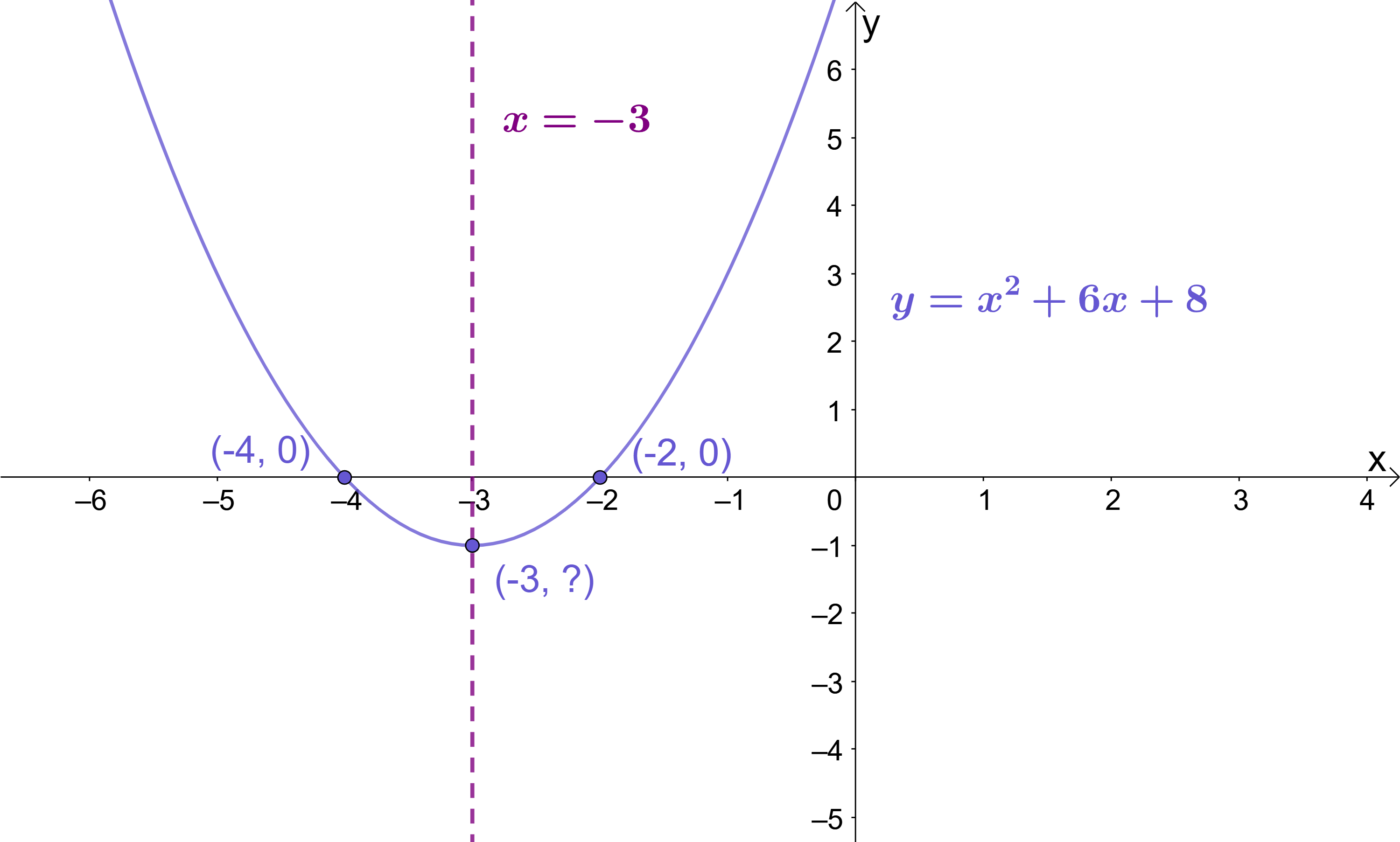
Because quadratics are symmetric curves, the line of symmetry runs through the mid-point of the roots. In the graph of y=x^{2}+6x+8, it is easy to see that the line of symmetry x=-3 runs through the mid-point of the roots which lie at (-4, 0) and (-2, 0):
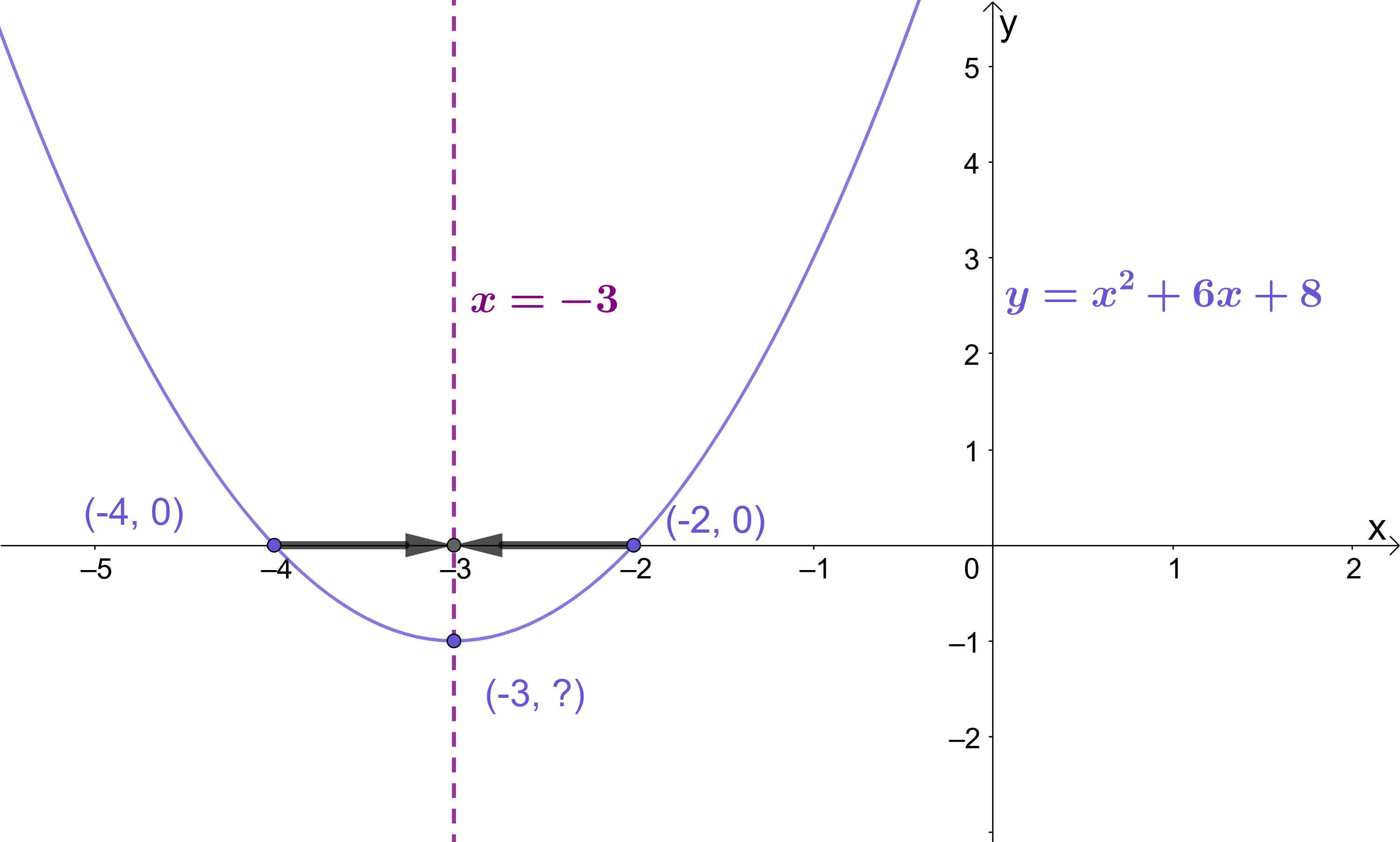
The quadratic y=x^{2}+6x+8 has roots at (-4, 0) and (-2, 0). With simple roots like these, it’s not difficult to tell that the mid-point of these roots is (-3, 0), but if the numbers were trickier, you’d probably need a formula to help you. Fortunately, one such formula exists:
The \boldsymbol{x}-coordinate of the mid-point of two roots can be calculated as the average of the two roots:
\begin{aligned}\boldsymbol{x_{mid-point}=\frac{x_{1}+x_{2}}{2}}\end{aligned}
Where \boldsymbol{x_{1}} and \boldsymbol{x_{2}} are the \boldsymbol{x}-coordinates of the first and second roots respectively.
Since we are dealing with roots (which always have a zero as the y-coordinate), we only need to bother calculating the the x-coordinate.
Testing this new formula out on the roots (-4, 0) and (-2, 0) confirms that the midpoint is indeed (-3, 0):
\begin{aligned}x_{mid-point}&=\frac{x_{1}+x_{2}}{2} \\[12pt]x_{mid-point}&=\frac{-4+(-2)}{2} \\[12pt]x_{mid-point}&=\frac{-4-2}{2} \\[12pt]x_{mid-point}&=\frac{-6}{2} \\[12pt]x_{mid-point}&=-3\end{aligned}
However, since the line of symmetry of a quadratic runs through the mid-point of the roots as well as the turning point, the turning point and the mid-point of the roots must have the same \boldsymbol{x}-coordinate.
We can therefore change our formula slightly to say:
The \boldsymbol{x}-coordinate of the turning point of a quadratic can be calculated as the average of its two roots:
\begin{aligned}\boldsymbol{x_{TP}=\frac{x_{1}+x_{2}}{2}}\end{aligned}
Where \boldsymbol{x_{1}} and \boldsymbol{x_{2}} are the \boldsymbol{x}-coordinates of the first and second roots respectively.
So we’re halfway there – we now know how to find the x-coordinate of a quadratic’s turning point (assuming we know the roots, as we need these to calculate it when we’re using this method!)
Of course now we need to calculate the y-coordinate of the turning point – but this is the easy part! Remember: every \boldsymbol{x} has a \boldsymbol{y} that goes with it. For the quadratic in this example y=x^{2}+6x+8, we’ve already calculated that x_{TP}=-3, so we simply substitute this into the equation of the quadratic to calculate the corresponding y value that goes with it (i.e. y_{TP}, the y-coordinate of the turning point):
\begin{aligned}y&=x^{2}+6x+8 \\[12pt]y_{TP}&=x_{TP}^{2}+6x_{TP}+8 \\[12pt]y_{TP}&=(-3)^{2}+6(-3)+8 \\[12pt]y_{TP}&=9-18+8 \\[12pt]y_{TP}&=-1\end{aligned}
Therefore, the turning point of the quadratic y=x^{2}+6x+8 lies at (x_{TP}, y_{TP})=(-3, -1). Incorporating a grid into the sketch of y=x^{2}+6x+8 from earlier, we can clearly see that this is the correct turning point:
Completing the Square
No doubt you will have noticed that there is a very clear limitation to the “mid-point of roots method” discussed in the section above – how could you use that method if the quadratic didn’t have any roots for you to work with? There are plenty of quadratics which don’t have roots, but all quadratics do have a turning point, so there must be a way to find the turning points of these quadratics without using roots!
Completing the Square is a more powerful technique for finding the turning point of a quadratic. Completing the Square works for all quadratics, including those which do not have roots.
By now you are accustomed to working with quadratics which are in the standard form of the General Equation y=ax^{2}+bx+c. When a quadratic is in the form y=ax^{2}+bx+c, you can easily read off both its nature and y-intercept, and you can use factorisation or the Quadratic Formula to find its roots. However, there is no quick way to take a quadratic in the form y=ax^{2}+bx+c and read off its turning point. To figure out the turning point requires more work (as we saw above).
Completing the Square is a process which takes a quadratic in the form of the General Equation:
\boldsymbol{y=ax^{2}+bx+c}
And transforms it into a quadratic of the form:
\boldsymbol{y=(x+p)^{2}+q}
In which the turning point can then easily be extracted as \boldsymbol{(-p, q)}.
Below is a summary of the two forms and the information they each reveal about a specific quadratic:

To transform a quadratic from y=ax^{2}+bx+c form into y=(x+p)^{2}+q form, we Complete the Square.
Before Completing the Square, make sure the \boldsymbol{a} coefficient (the number in front of the \boldsymbol{x^{2}} term) is 1. Only the more complicated examples have a coefficients other that 1 (refer to example 3 in the next topic for an example of this type). When you are ready to Complete the Square, the steps are as follows:
1) Open a bracket and put an \boldsymbol{x} term at the front
2) Add half the \boldsymbol{b} coefficient, then close the bracket and square it
3) Separately, multiply out the new bracket and see what constant you have (in most cases, this will not be the same as the constant the quadratic had in its original form, i.e. the \boldsymbol{c} coefficient)
4) Make an adjustment (add or subtract a number) to ensure the constant ultimately works out the same as the original \boldsymbol{c} coefficient
5) Once the quadratic is in \boldsymbol{y=(x+p)^{2}+q} form, extract the turning point as \boldsymbol{(-p, q)}
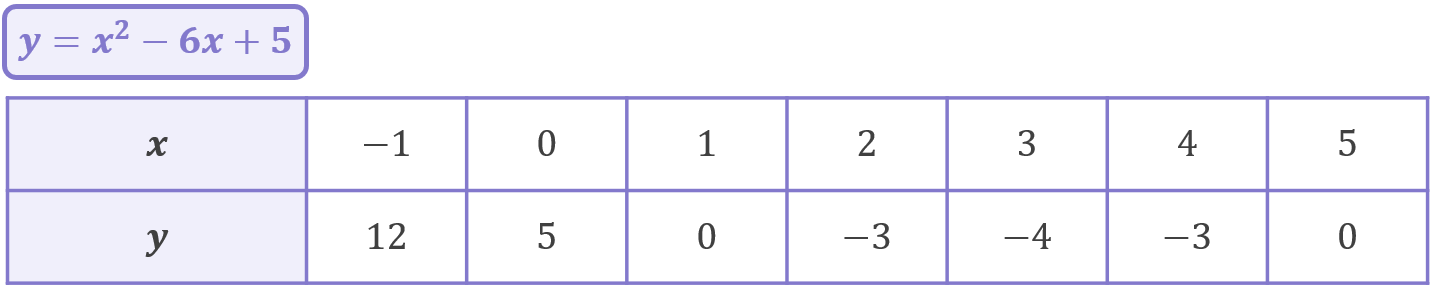
This process is best illustrated with a detailed worked example. Let’s Complete the Square to find the turning point of y=x^{2}-6x+5.
Before Completing the Square, we need to make sure the a coefficient (the number in front of the x^{2} term) is 1. Since the a coefficient of y=x^{2}-6x+5 is already 1, we don’t have to worry about this in this case.
Let’s now Complete the Square on y=x^{2}-6x+5:
1) Open a bracket and put an \boldsymbol{x} term at the front
\begin{aligned}y&=(x\end{aligned}
2) Add half the \boldsymbol{b} coefficient, then close the bracket and square it
As the b coefficient is -6, half of this is -3:
\begin{aligned}y&=(x-3)^{2}\end{aligned}
3) Separately, multiply out the new bracket and see what constant you have
\begin{aligned}y&=(x-3)^{2} \\[12pt]y&=(x-3)(x-3) \\[12pt]y&=x^{2}-3x-3x+9 \\[12pt]y&=x^{2}-6x+9\end{aligned}
Comparing y=x^{2}-6x+9 to the original quadratic y=x^{2}-6x+5, notice that the first and second terms are the same (both have an x^{2} and a -6x) but the constant at the back (the c coefficient) is off: we have +9 when we should have +5. We fix this in step four:
4) Make an adjustment (add or subtract a number) to ensure the constant ultimately works out the same as the original \boldsymbol{c} coefficient
We have +9 when we should have +5, so we must subtract 4:
\begin{aligned}y&=(x-3)^{2}-4\end{aligned}
Before including the -4, when we expanded the brackets the coefficient worked out as +9. Now, if we expand the brackets again, subtracting 4 will give us the correct c coefficient of +5:
\begin{aligned}y&=(x-3)^{2}-4 \\[12pt]y&=(x-3)(x-3)-4 \\[12pt]y&=x^{2}-3x-3x+9-4 \\[12pt]y&=x^{2}-6x+5\end{aligned}
Expanding y=(x-3)^{2}-4 returns the original quadratic y=x^{2}-6x+5.
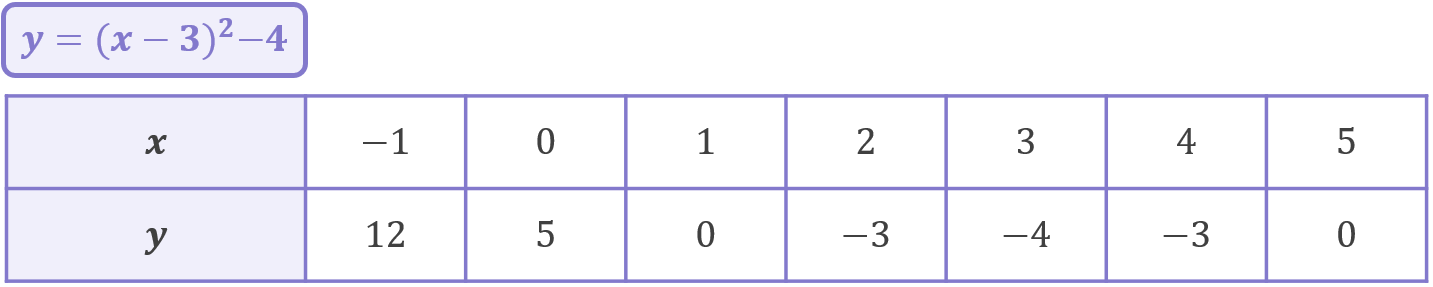
We have now successfully Completed the Square, transforming y=x^{2}-6x+5, which is in the form y=ax^{2}+bx+c, into y=(x-3)^{2}-4, which is in the form y=(x+p)^{2}+q:

5) Once the quadratic is in \boldsymbol{y=(x+p)^{2}+q} form, extract the turning point as \boldsymbol{(-p, q)}
We have successfully transformed y=x^{2}-6x+5 into y=(x-3)^{2}-4. Comparing y=(x-3)^{2}-4 to the general Complete the Square form:
\begin{aligned}y&=(x-3)^{2}-4 \\[12pt]y&=(x+p)^{2}+q\end{aligned}
We can extract that p=-3 and q=-4. Now we can simply state the turning point:
The turning point of a quadratic in y=(x+p)^{2}+q form is (-p, q). Therefore, the turning point of y=(x-3)^{2}-4 is (3, -4).
Let’s be very clear that in the example above all we have done is transform y=x^{2}-6x+5 into y=(x-3)^{2}-4. Basically, we have changed the way the quadratic is written such that it offers us different information, but we have not changed the underlying quadratic itself at all.
This is sort of like having two fractions, let’s say \large\frac{4}{2} and \large\frac{6}{3}. Both of these are just equal to 2 aren’t they? So they offer us different information, but the underlying information in each fraction is exactly the same.
Transforming y=x^{2}-6x+5 into y=(x-3)^{2}-4 has not changed the underlying quadratic at all – it has only changed the way it is written. If you populate a coordinate table for each version of the quadratic, you can see that they have exactly the same coordinates, so if you were to graph them, you’d just get the exact same graph twice!
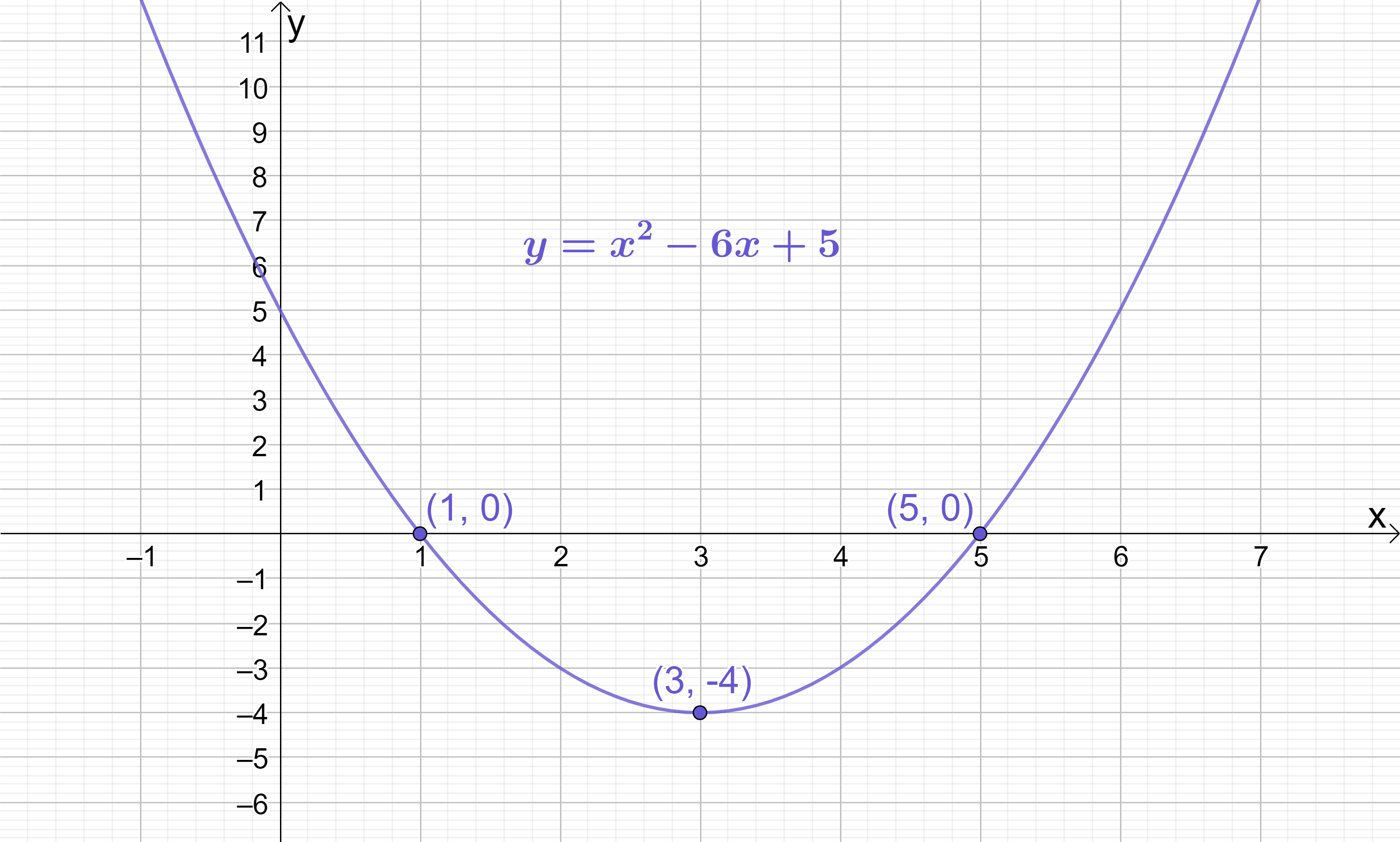
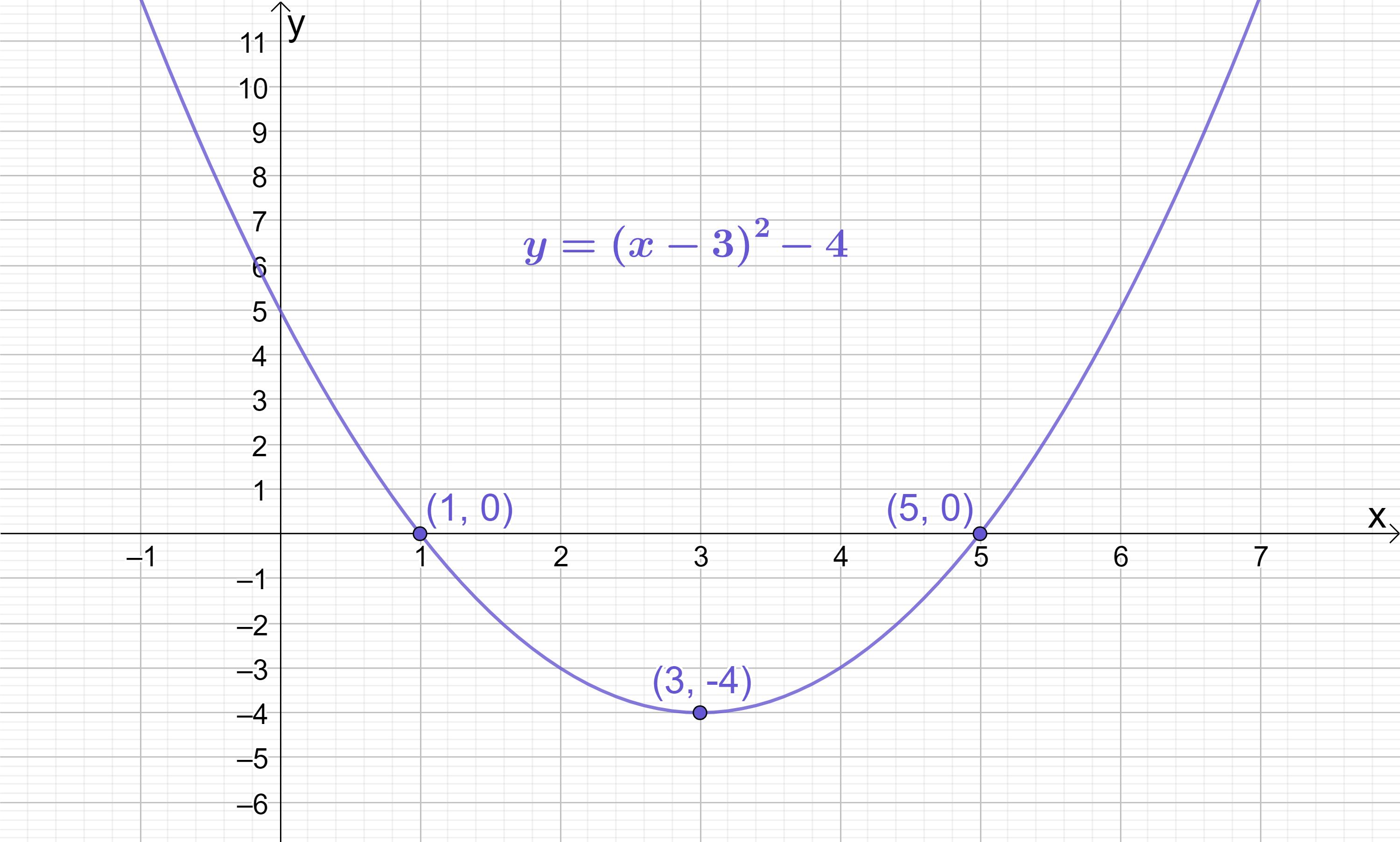
The graphs above also quite clearly confirm that the turning point of y=(x-3)^{2}-4 is indeed (3, -4).
Completing the Square can be a little tricky to get your head around at first, but with practice it really does become easier. Try not to get too caught up in the technique itself; keep it simple and always remember what the whole point of Completing the Square is in the first place:
Completing the Square is a process that transforms a quadratic in the form of the General Equation:
\boldsymbol{y=ax^{2}+bx+c}
Into a quadratic of the form:
\boldsymbol{y=(x+p)^{2}+q}
The benefit of writing a quadratic in the form \boldsymbol{y=(x+p)^{2}+q} is that you can very easily extract the quadratic’s turning point.
The turning point of a quadratic in the form \boldsymbol{y=(x+p)^{2}+q} lies at \boldsymbol{(-p, q)}.
Key Outcomes
Because quadratics are symmetric curves, the line of symmetry runs through the mid-point of the roots.
Since the line of symmetry of a quadratic runs through the mid-point of the roots as well as the turning point, the turning point and the mid-point of the roots must have the same x-coordinate.
The x-coordinate of the turning point can be calculated using the mid-point of roots formula:
\begin{aligned}x_{TP}=\frac{x_{1}+x_{2}}{2}\end{aligned}
Where x_{TP} is the x-coordinate of the turning point, and x_{1} and x_{2} are the x-coordinates of the first and second roots respectively.
To calculate the y-coordinate of the turning point (y_{TP}), substitute x_{TP} into the equation of the quadratic.
Always state turning points in full coordinate form: (x_{TP}, y_{TP})
Completing the Square is a more powerful tool for finding the turning point of a quadratic than the “mid-point of roots method” because Completing the Square works for all quadratics, including those which do not have roots.
Completing the Square is a process which takes a quadratic in standard form y=ax^{2}+bx+c and transforms it into a quadratic of the form y=(x+p)^{2}+q, where the turning point can then easily be extracted as (-p, q).
Before Completing the Square, make sure the a coefficient (the number in front of the x^{2} term) is 1. When you are ready to Complete the Square, the steps are as follows:
1) Open a bracket and put an x term at the front
2) Add half the b coefficient, then close the bracket and square it
3) Separately, multiply out the new bracket and see what constant you have (in most cases, this will not be the same as the constant the quadratic had in its original form, i.e. the c coefficient)
4) Make an adjustment (add or subtract a number) to ensure the constant ultimately works out the same as the original c coefficient
5) Once the quadratic is in y=(x+p)^{2}+q form, extract the turning point as (-p, q)
Completing the Square simply changes the way a quadratic is written such that it offers us different information (i.e. the turning point), but it does not change the underlying quadratic itself at all.