What are Trigonometric Identities?

Trigonometric identities are equations which define relationships, or “equalities”, between trigonometric functions. Quite simply, trigonometric identities are used to simplify expressions involving trigonometric functions to make them easier to work with. There are a huge number of identities out there, but fortunately at National 5 level there are only two you are expected to know:

A quick point on the notation used in Identity 2 – \boldsymbol{\sin^{2}x} should be pronounced “sine squared x” and it means \boldsymbol{\sin{x}} multiplied by itself. Therefore, \sin^{2}x=(\sin{x})^{2}=\sin{x}\times\sin{x} – these all mean the same thing, but \sin^{2}x is the accepted notation.

At first glance these identities (or relationships) probably won’t make a lot of sense. Identity 1 for example says that if you take a \sin{x} function and divide it by a \cos{x} function, you’ll get a \tan{x} function. Well I don’t know about you, but that doesn’t seem like an obvious result to me… However, if we return to the basic definitions of these functions then these identities actually become pretty straightforward to understand.

Recall the underlying definitions of the basic trigonometric functions, often remembered using the mnemonic SOH CAH TOA:

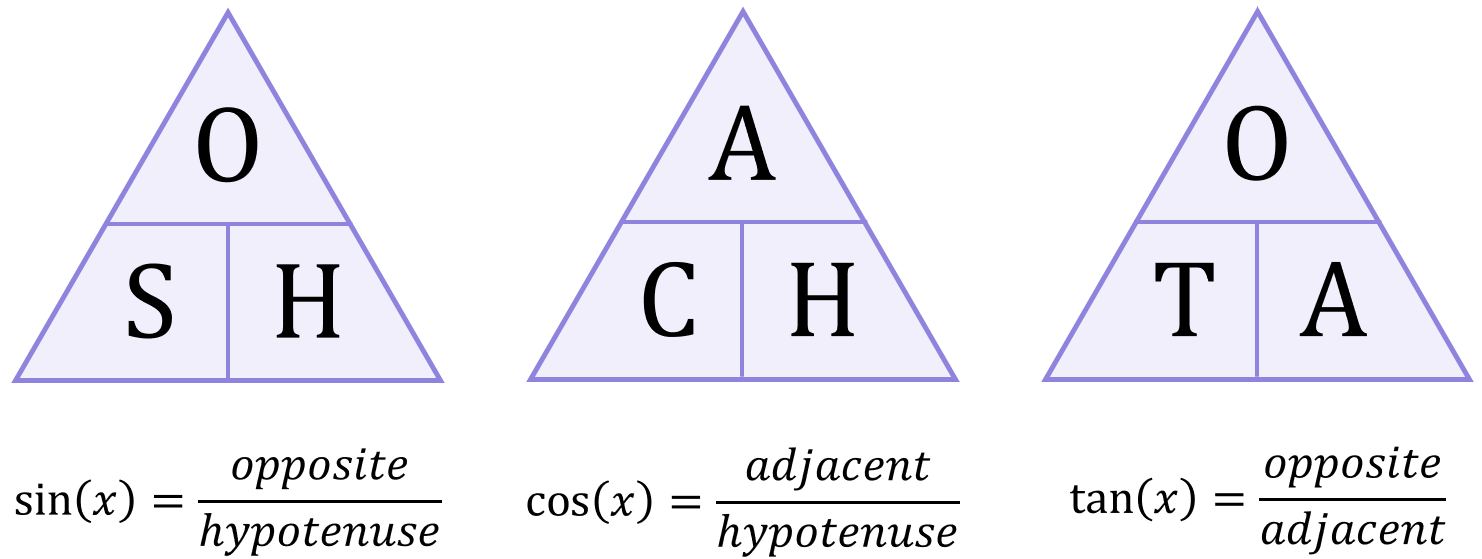
To keep things neat, let’s shorten the terms to opposite=o, adjacent=a and hypotenuse=h, giving:

\begin{aligned}&\sin{x}=\frac{o}{h}   &   &\cos{x}=\frac{a}{h}   &   &\tan{x}=\frac{o}{a}\end{aligned}

Using these definitions, we can easily derive the two identities ourselves. Let’s start with Identity 1:

\begin{aligned}&\boldsymbol{\textbf{Identity 1:}     \frac{\sin{x}}{\cos{x}}=\tan{x}}\end{aligned}

According to Identity 1, if we take \sin{x} and divide it by \cos{x} we should get \tan{x}. Well is this true or not? Using the underlying definitions, you can prove to yourself that this is actually true (don’t worry, you DO NOT have to know this proof for the exam):

\begin{aligned}\frac{\sin{x}}{\cos{x}}&=\Large\frac{\frac{o}{h}}{\frac{a}{h}} \\[16pt]&=\frac{o}{h}\times\frac{h}{a} \\[12pt]&=\frac{o\sout h}{a\sout h} \\[12pt]&=\frac{o}{a}=\tan{x}\end{aligned}

If you’re still not convinced, you can always test out the identity for yourself. All you have to do is pick a value for x, evaluate the functions using a calculator and see if the identity holds true.

Suppose x=30^\circ, then:

\begin{aligned}\sin{30}&=\frac{1}{2} \\[12pt]\cos{30}&=\frac{\sqrt{3}}{2} \\[12pt]\tan{30}&=\frac{1}{\sqrt{3}}\end{aligned}

Now if you divide the \sin{30} and \cos{30} results:

\begin{aligned}\frac{\sin{30}}{\cos{30}}&=\large\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}} \\[16pt]&=\frac{1}{2}\times\frac{2}{\sqrt{3}} \\[12pt]&=\frac{\sout2}{\sout2\sqrt{3}} \\[12pt]&=\frac{1}{\sqrt{3}}=\tan{30}\end{aligned}

Then you end up with the \tan{30} result!

Try picking another value of x – any value will work, it doesn’t need to be an exact value like 30^\circ.

Suppose this time x=62.1^\circ, then:

\begin{aligned}\sin{62.1}&=0.884 \\[12pt]\cos{62.1}&=0.468 \\[12pt]\tan{62.1}&=1.889\end{aligned}

If you now divide the \sin{62.1} and \cos{62.1} results:

\begin{aligned}\frac{\sin{62.1}}{\cos{62.1}}&=\frac{0.884}{0.468} \\[12pt]&=1.889=\tan{62.1}\end{aligned}

Then once again you end up with the equivalent tangent result!

You can use a very similar approach to prove Identity 2:

 \begin{aligned}&\boldsymbol{\textbf{Identity 2:}     \sin^{2}x+\cos^{2}x=1}\end{aligned}

According to Identity 2, if we take \sin{x} and square it, take \cos{x} and square it, and add these two results together, we should get 1. Again, definitely not the most obvious result in the world… but using the underlying definitions, you can prove to yourself that this is actually true (again, you DO NOT have to know this proof for the exam):

\begin{aligned}\sin^{2}x+\cos^{2}x&=\left(\frac{o}{h}\right)^{2}+\left(\frac{a}{h}\right)^{2} \\[12pt]&=\frac{o^{2}}{h^{2}}+\frac{a^{2}}{h^{2}} \\[12pt]&=\frac{o^{2}+a^{2}}{h^{2}}\end{aligned}

Recall by Pythagoras’ Theorem that a^{2}=b^{2}+c^{2}, so for the below triangle:

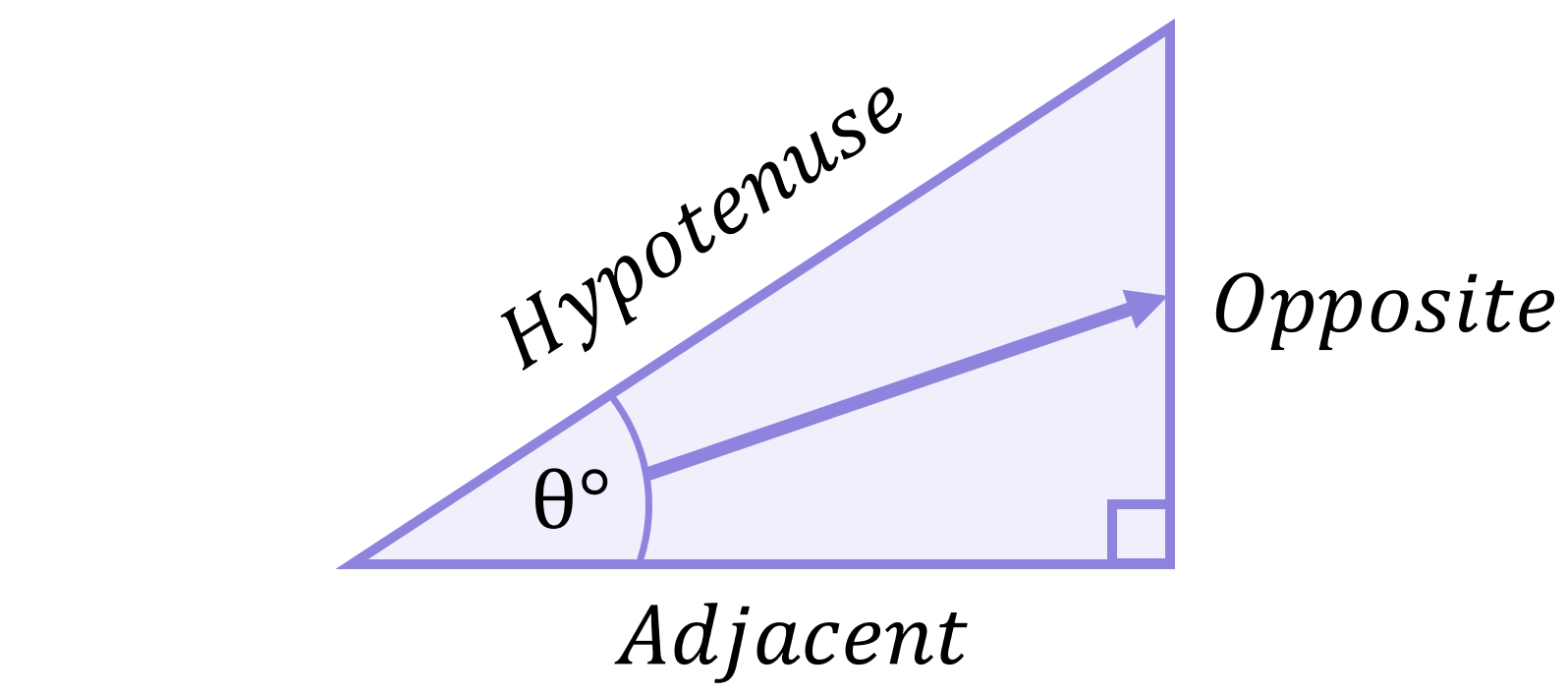
\begin{aligned}hypotenuse^{2}&=opposite^{2}+adjacent^{2} \\[12pt]h^{2}=o^{2}+a^{2}\end{aligned}

And with this we can continue our working:

\begin{aligned}\sin^{2}x+\cos^{2}x&=\left(\frac{o}{h}\right)^{2}+\left(\frac{a}{h}\right)^{2} \\[12pt]&=\frac{o^{2}}{h^{2}}+\frac{a^{2}}{h^{2}} \\[12pt]&=\frac{o^{2}+a^{2}}{h^{2}} \\[12pt]&=\frac{h^{2}}{h^{2}}=1\end{aligned}

As ever, if you’re not quite convinced of this then give it a go yourself – pick a value for x, evaluate the functions using a calculator and see if the identity holds true.

As an example, suppose x=60^\circ:

\begin{aligned}\sin{60}&=\frac{\sqrt{3}}{2}     &      \cos{60}&=\frac{1}{2} \\[24pt]\sin^{2}60&=\left(\frac{\sqrt{3}}{2}\right)^{2}     &      \cos^{2}60&=\left(\frac{1}{2}\right)^{2} \\[16pt]&=\frac{3}{4}     &    &=\frac{1}{2}\end{aligned}

And therefore:

\begin{aligned}\sin^{2}x+\cos^{2}x&=\sin^{2}60+\cos^{2}60 \\[6pt]&=\left(\frac{\sqrt{3}}{2}\right)^{2}+\left(\frac{1}{2}\right)^{2} \\[16pt]&=\frac{3}{4}+\frac{1}{4} \\[14pt]&=\frac{3+1}{4}=\frac{4}{4}=1\end{aligned}

As you can see, the identity has held true.

What I’ve laid out here is definitely not simple stuff, so do not worry if it’s a little bit difficult to follow at first. In this explanation I’ve gone into deeper detail than you need for your exam, but if you take your time to understand these workings it really will connect the dots and clarify the relationships between the trig functions (which will be extremely useful to you at Higher level!)

Hopefully you found this explanation insightful; personally, when I saw these proofs for the first time it was a total “penny drop” moment that really helped me understand identities! But if it was a bit challenging then do not worry about it! The only things you really need to take from this topic at a minimum are the identities themselves – remember these, and you have everything you need for your exam.

In the next topic, we will focus on how these identities are used in practice in exam-style questions.