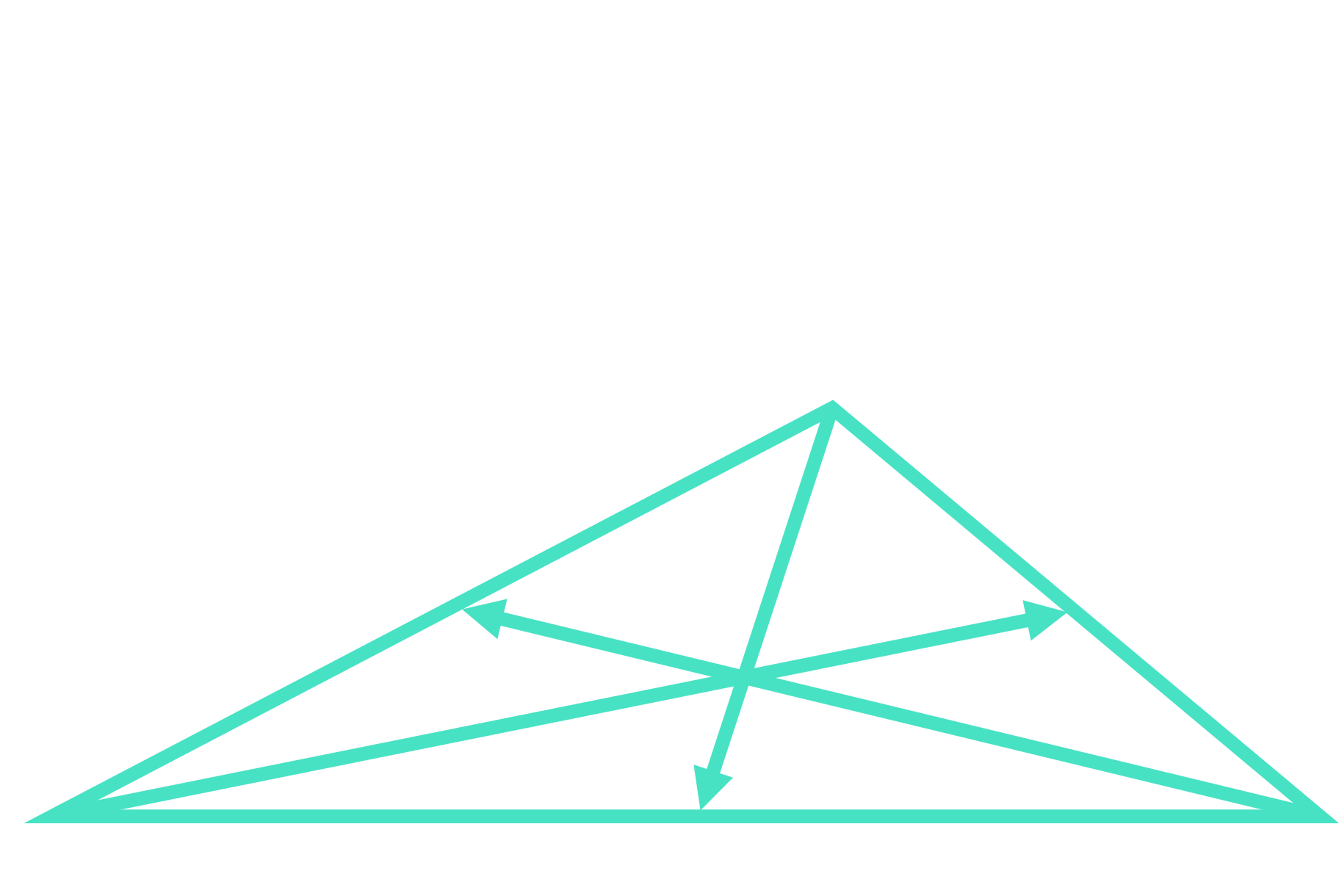
What is The Sine Rule?
The first thing to get right when working with non-right-angled triangles is the labelling convention. Without proper labelling, the formulas will not work!
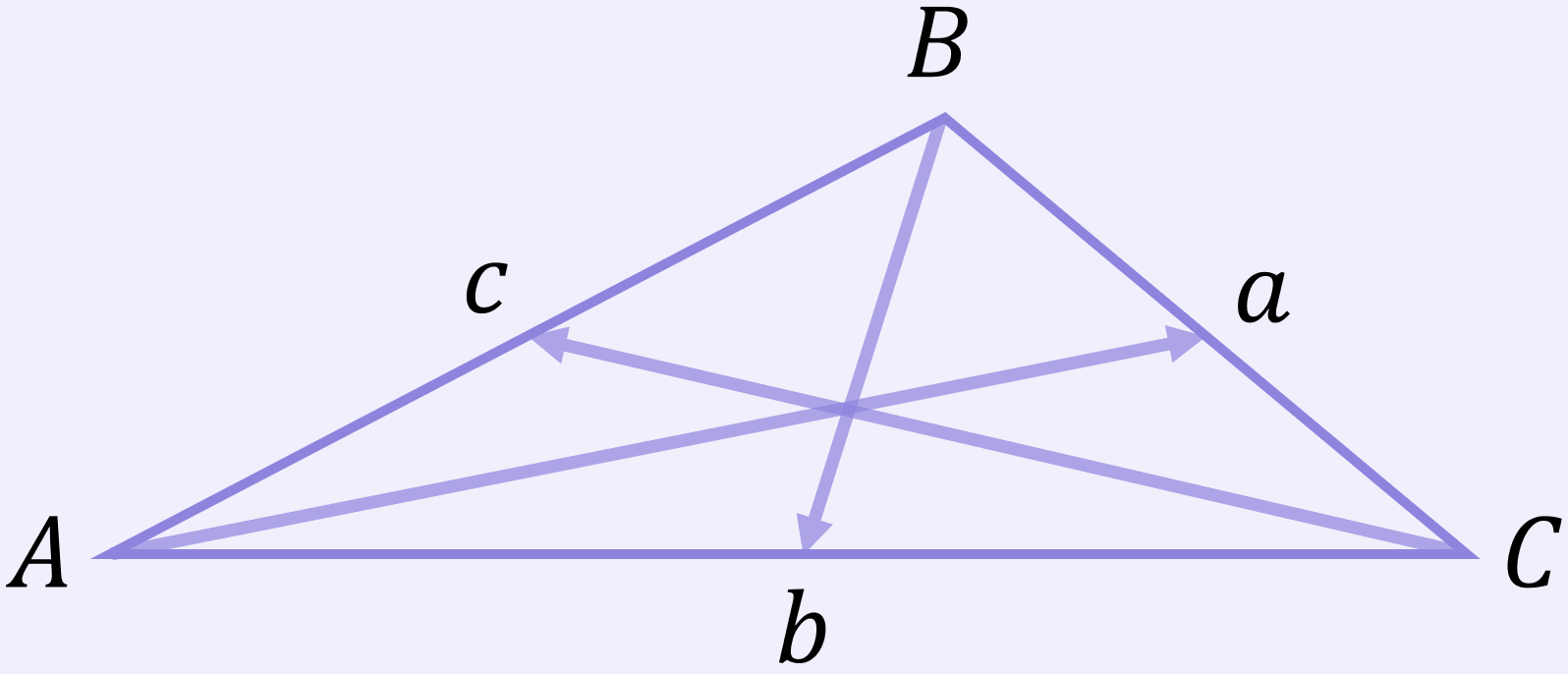
The convention when labelling a non-right-angled triangle is:
- For angles, use upper case labels – A, B and C; and
- For sides, use lower case labels – a, b and c
And crucially:
- Side a must be opposite angle A;
- Side b must be opposite angle B; and
- Side c must be opposite angle C
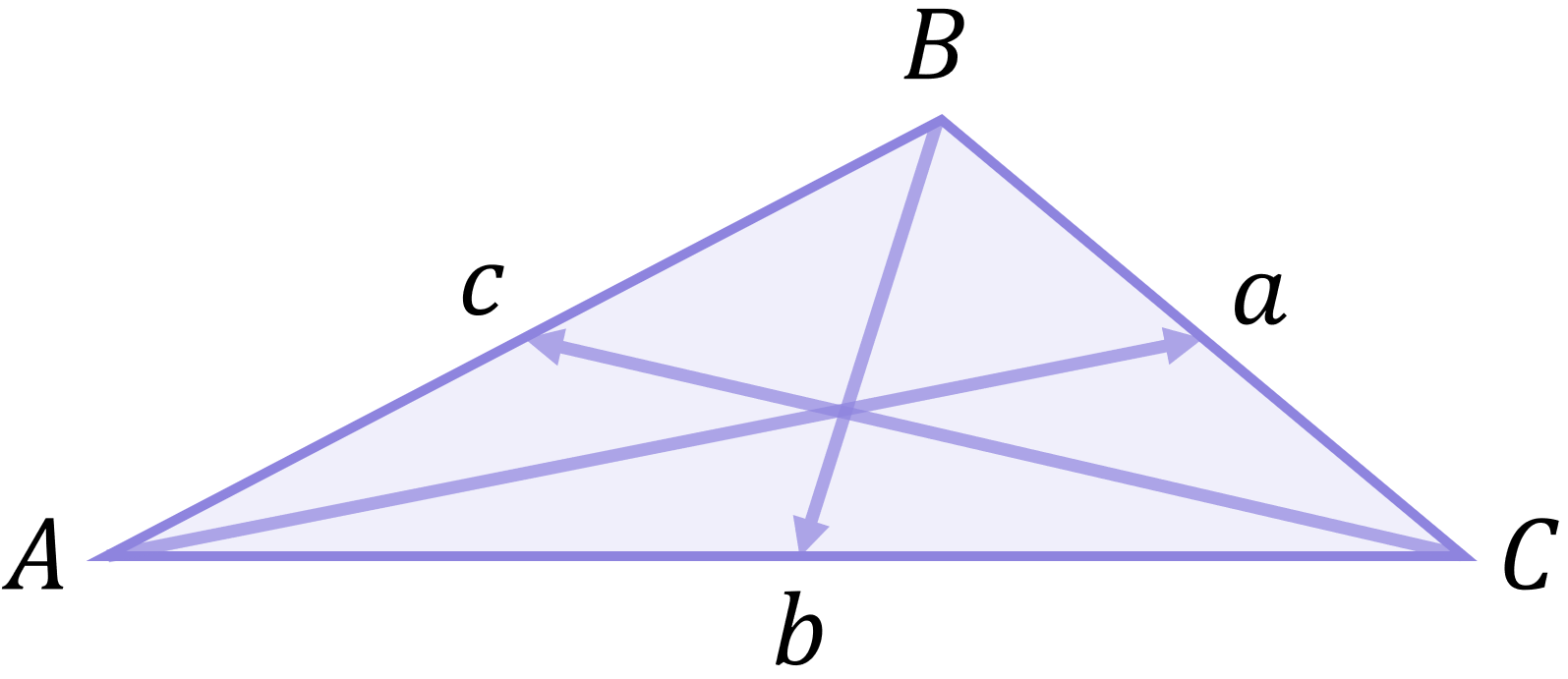
It is not important that the actual angle letters A, B and C and side letters a, b and c are used – different questions often use different labels and a certain question might for instance use letters P, Q and R for angles and letters p, q and r for the corresponding sides. But the key point here is that side p would be opposite angle P, side q would be opposite angle Q and side r would be opposite angle R.
With that out of the way, we can introduce the Sine Rule:
The Sine Rule for non-right-angled triangles is:
\begin{aligned}\boldsymbol{\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}}\end{aligned}
To use the Sine Rule, one corresponding side and angle pair must be known, plus one additional piece of information.
The Sine Rule gives us the ability to work out the angles and side lengths of non-right-angled triangles in certain, but not all, situations.
To use the Sine Rule, one corresponding side and angle pair must be known, plus one additional piece of information. A corresponding pair would be for example, side a plus angle A both being known, or side b plus angle B both being known, and so on. The other piece of information can be any of the remaining sides or angles.
The best way to understand when you can use the Sine Rule is, as with most things, by working through a few examples.
Using the Sine Rule to calculate side lengths
Calculate the length of the side labelled x:
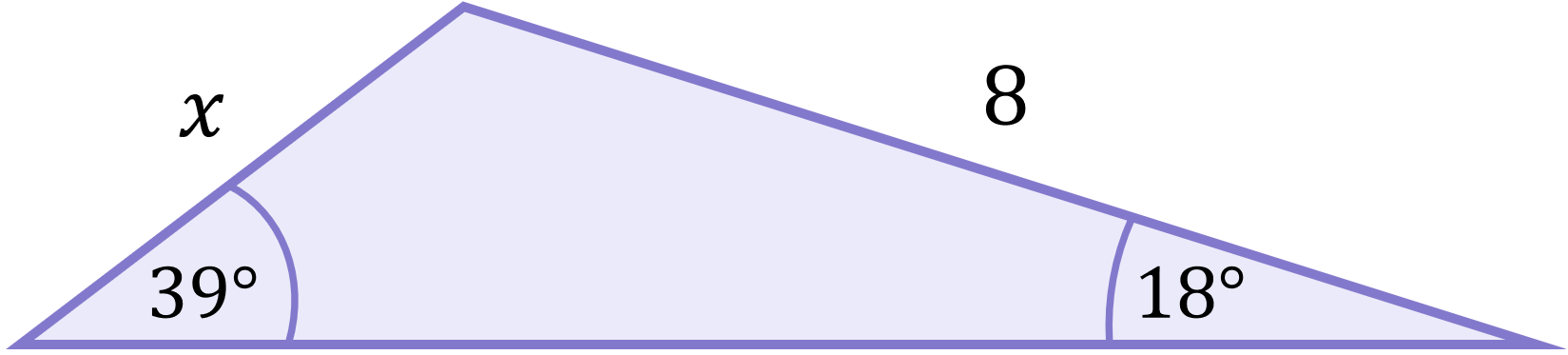
Clearly this triangle is non-right-angled, so we cannot use Pythagoras’ Theorem nor SOH CAH TOA to calculate x. Let’s try using the Sine Rule.
As always, our first priority should be to label the triangle’s sides and angles appropriately. As this triangle didn’t come with any labels of its own, we can make the labels up. For simplicity in situations like this, always use A, B and C. The order of the labelling does not matter, but of course you must make sure you match up angles to the correct corresponding sides:
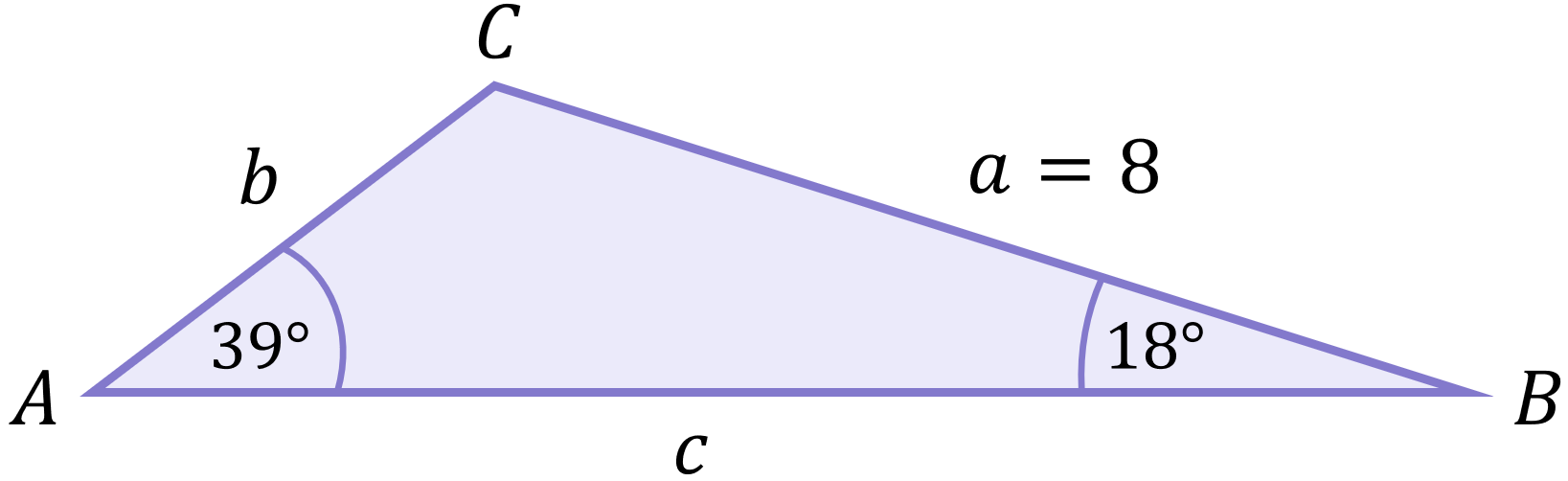
The side we wish to calculate, x, has been relabelled b (since it is opposite the angle we have chosen to label B).
Using a similar method as in the SOH CAH TOA section, known information is often “ticked”. For our triangle, we know the angles A and B, and we also know side a:
\begin{aligned}\frac{a \checkmark}{\sin{A} \checkmark}=\frac{b}{\sin{B} \checkmark}=\frac{c}{\sin{C}}\end{aligned}
Since one corresponding side and angle pair is known (side a and angle A), plus one additional piece of information (angle B) we are ready to use the Sine Rule.
Working with the first two fractions in the Sine Rule, we will be able to rearrange the terms to make b – the side we are trying to calculate – the subject of the equation:
\begin{aligned}\frac{a}{\sin{A}}&=\frac{b}{\sin{B}} \\[12pt]a\sin{B}&=b\sin{A} \\[12pt]\frac{a\sin{B}}{\sin{A}}&=b \\[12pt]b&=\frac{a\sin{B}}{\sin{A}}\end{aligned}
We know that a=8, A=39^\circ and B=18^\circ, so we can substitute these values into the equation:
\begin{aligned}b&=\frac{a\sin{B}}{\sin{A}} \\[12pt]b&=\frac{8\sin{18}}{\sin{39}} \\[12pt]b&=3.9\end{aligned}
Remember in the original triangle the side now labelled b was originally called x. Therefore, as a final answer you should state:
\begin{aligned}x&=3.9\end{aligned}
Using the Sine Rule to calculate angles
Find the size of the angle R:
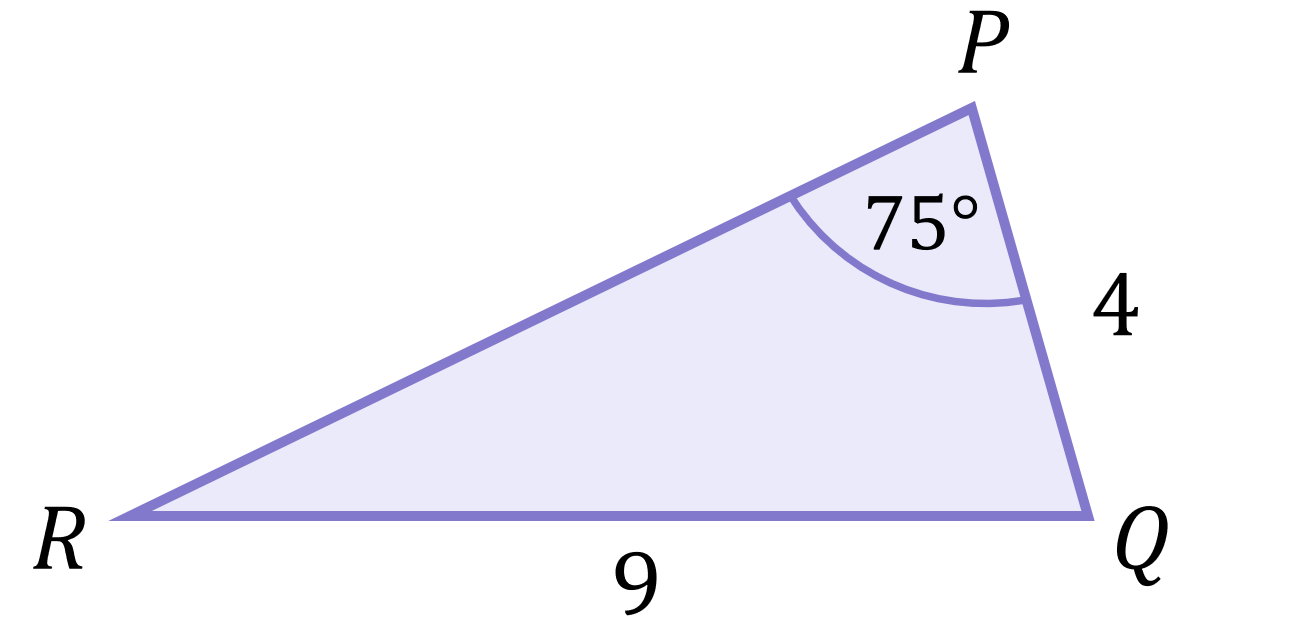
This triangle has already been labelled, so it is best to stick with these (this helps your examiner understand the sides and angles you’re referring to since you’re both using the same labelling convention). Now we label the sides and tick all the information we have:
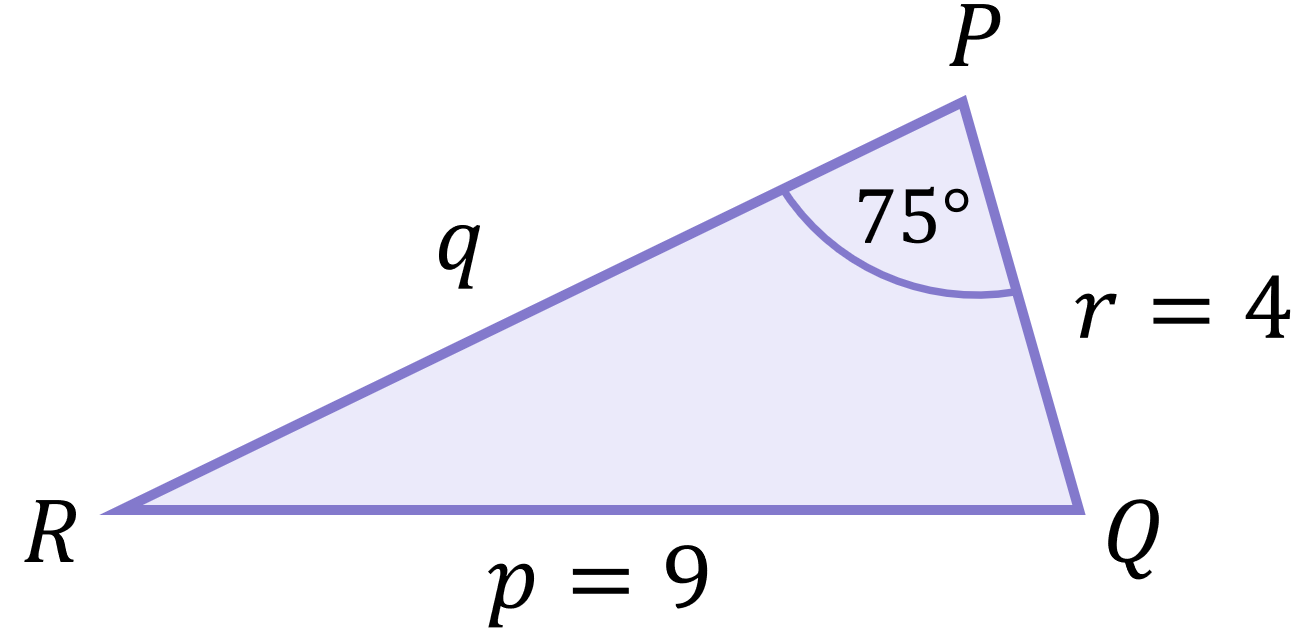
\begin{aligned}\frac{p \checkmark}{\sin{P} \checkmark}=\frac{q}{\sin{Q}}=\frac{r \checkmark}{\sin{R}}\end{aligned}
Since one corresponding side and angle pair is known (side p and angle P), plus one additional piece of information (side r) we are ready to use the Sine Rule.
Working with the first and third fractions (the ones that have ticks), we will be able to rearrange the terms to make R – the angle we are trying to calculate – the subject of the equation:
\begin{aligned}\frac{p}{\sin{P}}&=\frac{r}{\sin{R}} \\[12pt]p\sin{R}&=r\sin{P} \\[12pt]\sin{R}&=\frac{r\sin{P}}{p} \\[12pt]R&=\sin^{-1}\left(\frac{r\sin{P}}{p}\right)\end{aligned}
We know that p=9, r=4 and P=75^\circ, so we can substitute these values into the equation:
\begin{aligned}R&=\sin^{-1}\left(\frac{4\sin{75}}{9}\right) \\[12pt]R&=25.4^\circ\end{aligned}
When using the Sine Rule fails
The two applications we just discussed are typical of Sine Rule questions; there’s really no possible variations or ways to further complicate the rule, so the questions you will face in your exam will follow the template of the examples given. The hardest aspect of using the Sine Rule is actually having the skill and understanding to determine whether the Sine Rule can even be used in the first place. Take the following triangle for example:
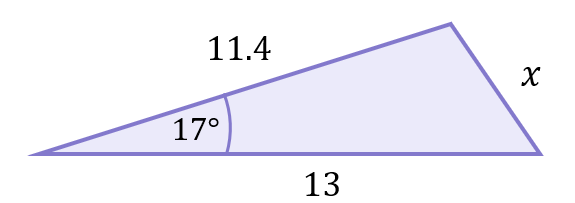
Can the Sine Rule be used to calculate the side labelled x? Relabelling the full triangle in the usual fashion (notice that x has been changed to a):
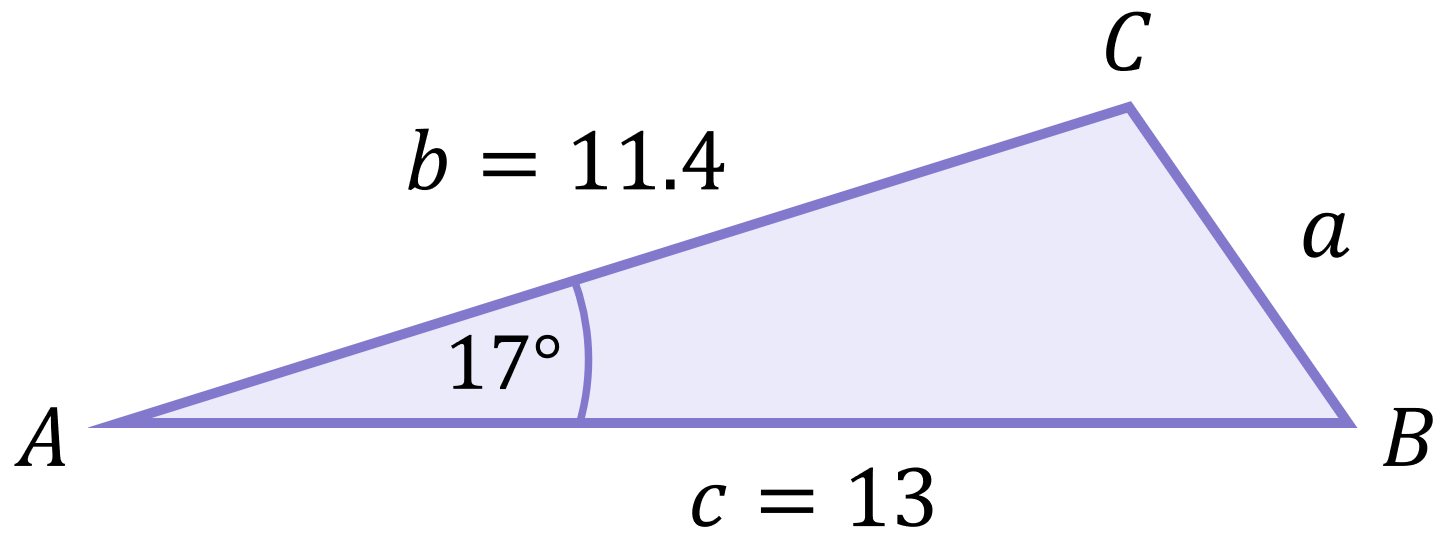
\begin{aligned}\frac{a}{\sin{A} \checkmark}=\frac{b \checkmark}{\sin{B}}=\frac{c \checkmark}{\sin{C}}\end{aligned}
We see that for this triangle we cannot use the Sine Rule since no corresponding side and angle pairs are known (no fraction has two ticks). If you attempted to calculate side a using the Sine Rule, you would reach an unsolvable equation:
\begin{aligned}\frac{a}{\sin{A}}&=\frac{b}{\sin{B}} \\[16pt]a\sin{B}&=b\sin{A} \\[12pt]a&=\frac{b\sin{A}}{\sin{B}}\end{aligned}
We know that b=11.4 and A=17^\circ, but we do not know angle B! So we are left with an equation with two unknowns:
\begin{aligned}a&=\frac{11.4\sin{17}}{\sin{B}}\end{aligned}
This cannot be solved. Because we did not have the right informational set up at the beginning, the Sine Rule has failed. In this case, a different rule for non-right-angled triangles – the Cosine Rule – is required to calculate side \boldsymbol{a} (we discuss this rule in the next topic).
Without a proper understanding of labelling conventions and the Sine Rule, you could mistakenly think the Sine Rule would work here and waste time trying to use it only to end up stuck with an unsolvable equation! But with a proper understanding of the Sine Rule, once you’ve correctly determined that the rule can be used (using the “tick” method detailed in the examples), then actually using the rule should be pretty straightforward.
Key Outcomes
The first thing to get right when working with non-right-angled triangles is the labelling convention. Without proper labelling, the formulas will not work!
The convention when labelling a non-right-angled triangle is:
- For angles, use upper case labels – A, B and C; and
- For sides, use lower case labels – a, b and c
And crucially:
- Side a must be opposite angle A;
- Side b must be opposite angle B; and
- Side c must be opposite angle C
The Sine Rule for non-right-angled triangles is:
\begin{aligned}\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}\end{aligned}
To use the Sine Rule, one corresponding side and angle pair must be known, plus one additional piece of information.
The hardest aspect of using the Sine Rule is actually having the skill and understanding to determine whether the Sine Rule can even be used in the first place. Get this right and the rest should flow fairly easily.