We have already learned that factorising can be used to find the roots of a quadratic. However, factorising is actually not the most powerful tool in the world as it is only really useful in the simplest of cases where the roots are nice, easy whole numbers. As you can imagine, in the real world the majority of quadratic equations don’t have simple whole number roots. Take for example the quadratic:

y=x^{2}+11x+5

This looks much the same as all the quadratics you have met thus far, and you may think that to find its roots it’s a simple matter of substituting y=0 into the equation and solving via factorisation to find the roots as usual. Clearly there are no common factors, and it doesn’t meet the criteria for difference of two squares, so if it factorises it must be a trinomial case, but if you try and factorise this into two brackets you may find this challenging! (Give it a try…)

If you struggled don’t worry – it is extremely difficult to factorise this into two brackets manually as the roots are not simple whole numbers! If we sketch this quadratic:

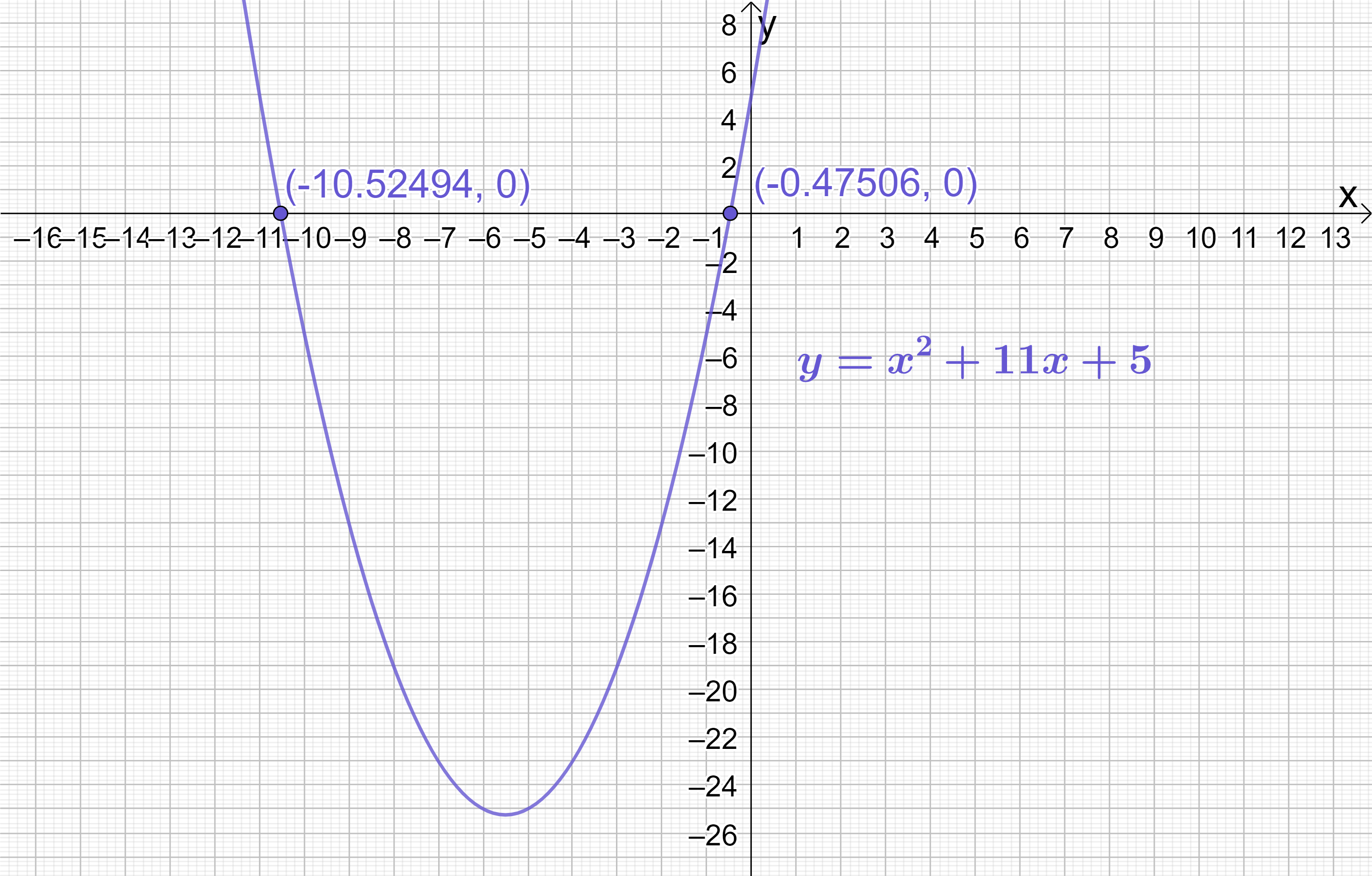
We can see that its roots actually lie at (-10.52494, 0) and (-0.47506, 0) (where I’ve rounded the roots to 5 decimal places). If you tried to figure that out using manual factorisation, let’s just say you’d be there a while…

So, we need a more powerful tool for calculating the roots of these more complex quadratics. Step in: the Quadratic Formula:

Previously we have used the technique of factorisation to calculate the roots of quadratics – that works perfectly well in many cases, and if it is possible to use factorisation then you should do so before considering any other technique. For more complex quadratics however, the Quadratic Formula is the only way to find the roots.

It looks complicated, but using the Quadratic Formula is actually fairly straightforward. The formula takes a, b and c as inputs on the RHS. Recall that a, b and c are just the coefficients of any quadratic written in the form of the General Equation y=ax^{2}+bx+c. So if for example we had the quadratic:

y=x^{2}-6x+8

Which has coefficients a=1, b=-6 and c=8, we can substitute these values into the Quadratic Formula in order to find the roots:

\begin{aligned}x&=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a} \\[12pt]x&=\frac{-(-6)\pm\sqrt{(-6)^{2}-4(1)(8)}}{2(1)} \\[12pt]x&=\frac{6\pm\sqrt{36-32}}{2} \\[12pt]x&=\frac{6\pm\sqrt{4}}{2} \end{aligned}

At this point, we split the solution into two avenues – one exploring the + case, and one exploring the - case:

\begin{aligned}x&=\frac{6+\sqrt{4}}{2}     &\text{or}                x&=\frac{6-\sqrt{4}}{2} \\[12pt]x&=\frac{6+2}{2}     &\text{or}                x&=\frac{6-2}{2} \\[12pt]x&=\frac{8}{2}     &\text{or}                x&=\frac{4}{2} \\[12pt]x&=4     &\text{or}                x&=2\end{aligned}

Hence the quadratic y=x^{2}-6x+8 has roots at (2, 0) and (4, 0) (remember: at the roots, y always equals 0).

We can double check this is correct by finding the roots of y=x^{2}-6x+8 using factorisation instead. Substituting y=0 and factorising gives:

\begin{aligned}x^{2}-6x+8&=0 \\[8pt](x-2)(x-4)&=0 \\[8pt](x-2)=0    \text{or}     (x-4)&=0 \\[20pt]x-2&=0 \\[6pt]x&=2 \\[20pt]x-4&=0 \\[6pt]x&=4\end{aligned}

Which gives roots at (2, 0) and (4, 0) as before. Since the roots of y=x^{2}-6x+8 can be found using factorisation you would never actually need to use the Quadratic Formula on this quadratic, but as you can see, both methods lead to the same answer.

That begs the question: when are we supposed to use the Quadratic Formula, and when should we use factorising? Well, technically the Quadratic Formula can always be used to find the roots of a quadratic function (assuming the quadratic actually has roots that is, because some do not!), but you should always factorise first if it is possible to do so. In short, if you have tried to factorise and it cannot be done, use the Quadratic Formula instead to find the roots instead.

Another major giveaway that you should be using the Quadratic Formula is if you are asked to find roots to 1 or 2 decimal places. If you’re asked for that level of accuracy, basic factorisation isn’t going to cut it!

Suppose we had to find the roots of y=2x^{2}+5x-2 to 2 decimal places. In this example a=2, b=5 and c=-2. We can substitute these values into the Quadratic Formula to calculate the roots:

\begin{aligned}x&=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a} \\[12pt]x&=\frac{-(5)\pm\sqrt{(5)^{2}-4(2)(-2)}}{2(2)} \\[12pt]x&=\frac{-5\pm\sqrt{25+16}}{4} \\[12pt]x&=\frac{-5\pm\sqrt{41}}{4}\end{aligned}

Splitting into the + case and the - case, we have:

\begin{aligned}x&=\frac{-5+\sqrt{41}}{4}     &\text{or}                x&=\frac{-5-\sqrt{41}}{4} \\[12pt]x&=0.35     &\text{or}                x&=-2.85\end{aligned}

Hence the quadratic y=2x^{2}+5x-2 has roots at (0.35, 0) and (-2.85, 0).

Note that it is absolutely crucial to ensure that your quadratic is in the form of the General Equation \boldsymbol{y=ax^{2}+bx+c} before you try to use the Quadratic Formula to find its roots. If your quadratic is not in this form, you will extract incorrect values of a, b and c which will in turn lead to incorrect roots when substituted into the Quadratic Formula.

Suppose you were presented with the quadratic y-x^{2}-8x=9. Clearly, this is not in standard form. Before we attempt to find this quadratic’s roots, we must first rearrange as follows to make y the subject:

\begin{aligned}y-x^{2}-8x&=9 \\[12pt]y&=x^{2}+8x+9\end{aligned}

Now that the quadratic is in standard form, we can extract that a=1, b=8 and c=9. We can substitute these values into the Quadratic Formula to calculate the roots:

\begin{aligned}x&=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a} \\[12pt]x&=\frac{-(8)\pm\sqrt{(8)^{2}-4(1)(9)}}{2(1)} \\[12pt]x&=\frac{-8\pm\sqrt{64-36}}{2} \\[12pt]x&=\frac{-8\pm\sqrt{28}}{2}\end{aligned}

Splitting into the + case and the - case, we have:

\begin{aligned}x&=\frac{-8+\sqrt{28}}{2}     &\text{or}                x&=\frac{-8-\sqrt{28}}{2} \\[12pt]x&=-6.65     &\text{or}                x&=-1.35\end{aligned}

Hence the quadratic y=x^{2}+8x+9 has roots at (-6.65, 0) and (-1.35, 0).

As a final point of clarification, let’s be absolutely clear on the difference between the General Equation of a Quadratic Function and the Quadratic Formula (students have often confused the two over the years!)

The General Equation of a Quadratic Function (which was introduced in a previous topic) is:

\begin{aligned}y=ax^{2}+bx+c\end{aligned}

Think of this equation as describing the shape of the actual quadratic itself – it defines the exact curvature and position of any quadratic. If someone generally talks about the “equation” of a specific quadratic, they are referring to an equation in this form, such as y=x^{2}+8x+9 in the last example.

The Quadratic Formula (which was introduced for the first time in this topic), is:

\begin{aligned}x&=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\end{aligned}

This formula is explicitly used to calculate the roots (i.e. the x-intercepts) of quadratic functions. The inputs (a, b and c) used in this formula come from the “equation” of a specific quadratic, such as y=x^{2}+8x+9 in the last example, for which a=1, b=8 and c=9.