The first thing to get right when working with non-right-angled triangles is the labelling convention. Without proper labelling, the formulas will not work!

The convention when labelling a non-right-angled triangle is:

• For angles, use upper case labels – A, B and C; and
• For sides, use lower case labels – a, b and c

And crucially:

• Side a must be opposite angle A;
• Side b must be opposite angle B; and
• Side c must be opposite angle C

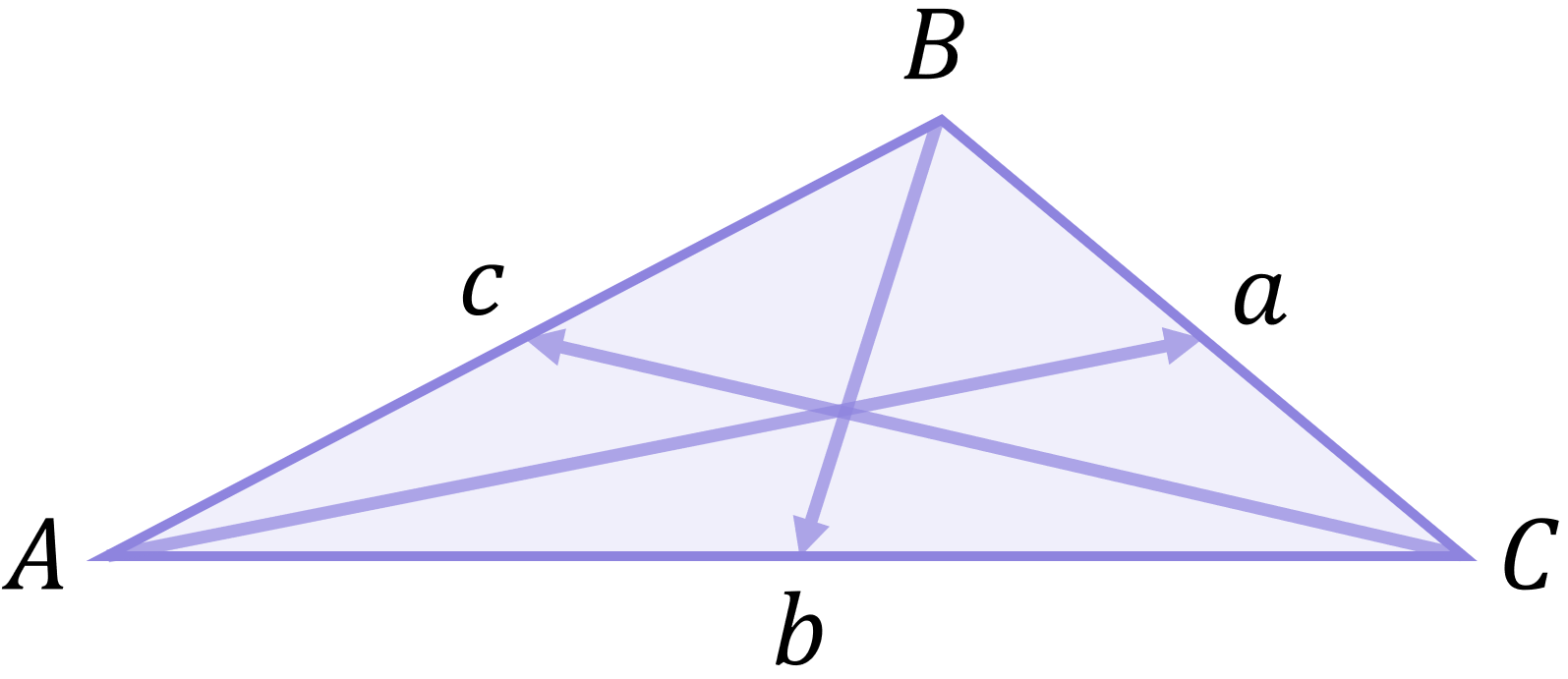
It is not important that the actual angle letters A, B and C and side letters a, b and c are used – different questions often use different labels and a certain question might for instance use letters P, Q and R for angles and letters p, q and r for the corresponding sides. But the key point here is that side p would be opposite angle P, side q would be opposite angle Q and side r would be opposite angle R.

With that out of the way, we can introduce the Cosine Rule: 

In non-right-angled trigonometry, the Cosine Rule steps in where the Sine Rule fails. In situations where you cannot use the Sine Rule to calculate lengths or angles, you will instead use the Cosine Rule (and vice versa).

To be clear, both formulas above represent the same Cosine Rule – one is simply a rearrangement of the other. Starting with Form 1, by making basic rearrangements:

\begin{aligned}a^{2}&=b^{2}+c^{2}-2bc\cos{A} \\[12pt]a^{2}+2bc\cos{A}&=b^{2}+c^{2} \\[12pt]2bc\cos{A}&=b^{2}+c^{2}-a^{2} \\[12pt]\cos{A}&=\frac{b^{2}+c^{2}-a^{2}}{2bc}\end{aligned}

We arrive at Form 2.

So why the two forms? Good question. The two forms of the Cosine Rule are applied in different scenarios (i.e. when different combinations of information about the triangle are available). Only one of the forms will be appropriate for a given scenario.

Notice that the forms as stated are set up to calculate either side a (Form 1 has a as its subject) or the angle A (Form 2 has \cos{A} as its subject). The two forms can alternatively be restated to have any of the other sides and angles as their subjects:

Form 2 is actually the easiest to understand, so let’s begin there.

First, we must establish when we are able to use Form 2 of the Cosine Rule:

If you look more closely at the formula for Form 2, this is actually kind of obvious since the RHS requires all sides (a, b and c) as inputs. Let’s see this in practice.

Calculate the size of angle A:

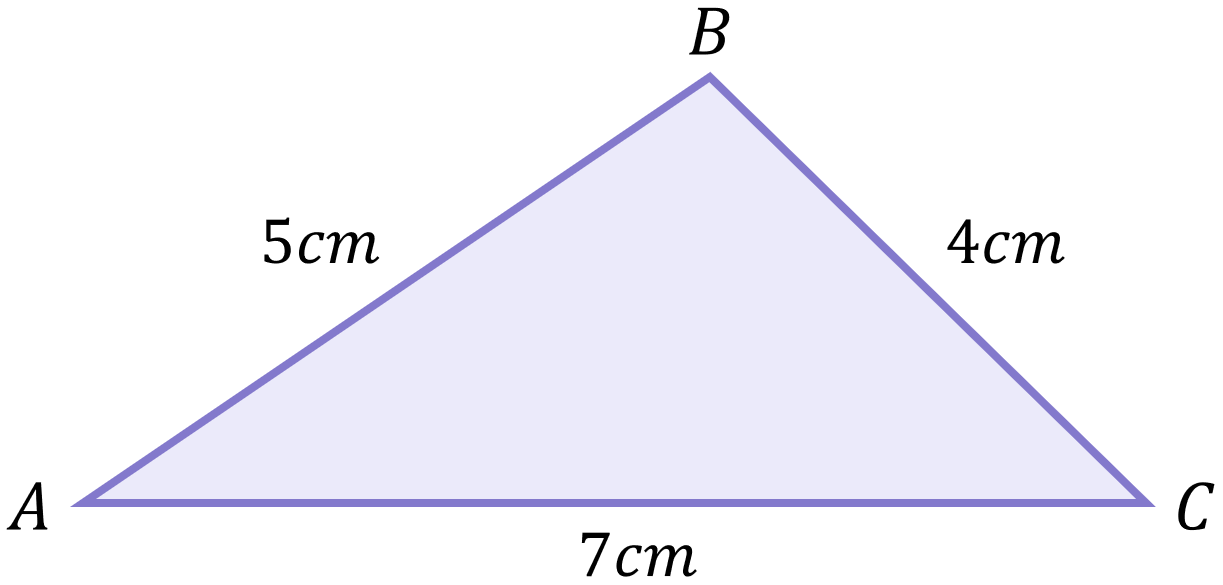
Since we know all the side lengths, we can use Form 2 of the Cosine Rule:

\begin{aligned}\cos{A}&=\frac{b^{2}+c^{2}-a^{2}}{2bc}\end{aligned}

We know that a=4, b=7 and c=5, so we can substitute these values:

\begin{aligned}\cos{A}&=\frac{(7)^{2}+(5)^{2}-(4)^{2}}{2(7)(5)} \\[12pt]\cos{A}&=\frac{49+25-16}{70} \\[12pt]\cos{A}&=\frac{58}{70} \\[12pt]A&=\cos^{-1}\left(\frac{58}{70}\right)\\[12pt]A&=34^\circ\end{aligned}

Calculate the size of angle R:

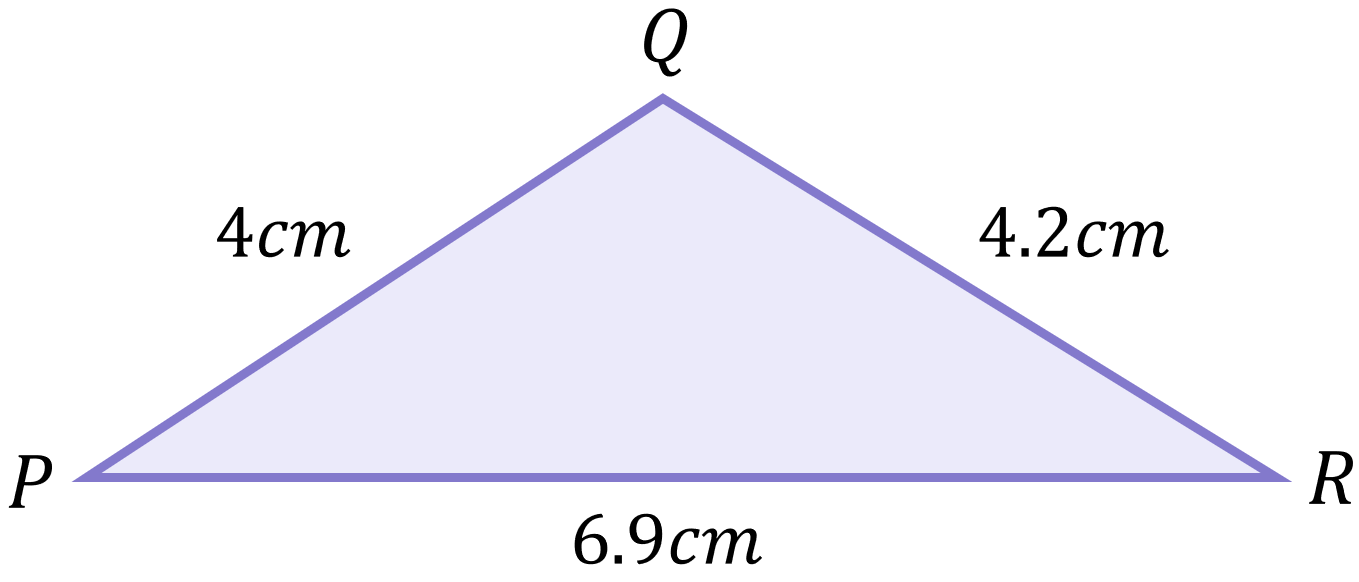
Since we know all the side lengths, we can use Form 2 of the Cosine Rule which we will re-brand with the labelling used for this triangle:

\begin{aligned}\cos{R}&=\frac{p^{2}+q^{2}-r^{2}}{2pq}\end{aligned}

We know that p=4.2, q=6.9 and r=4, so we can substitute these values:

\begin{aligned}\cos{R}&=\frac{(4.2)^{2}+(6.9)^{2}-(4)^{2}}{2(4.2)(6.9)} \\[12pt]\cos{R}&=\frac{17.6+47.6-16}{58} \\[12pt]\cos{R}&=\frac{49.2}{58} \\[12pt]R&=\cos^{-1}\left(\frac{49.2}{58}\right)\\[12pt]R&=32^\circ\end{aligned}

Now let’s take a closer look at Form 1 of the Cosine Rule.

Just as we did with Form 2, we must establish when we are able to use Form 1 of the Cosine Rule:

The above is not obvious just by looking at the formula for Form 1:

\begin{aligned}a^{2}=b^{2}+c^{2}-2bc\cos{A}\end{aligned}

From the formula, it is clear we need to know sides b and c plus angle A (i.e. all the RHS terms) in order to calculate side a. Looking at this set up for a real triangle, you can see this forms the “two sides plus the included angle” requirement:

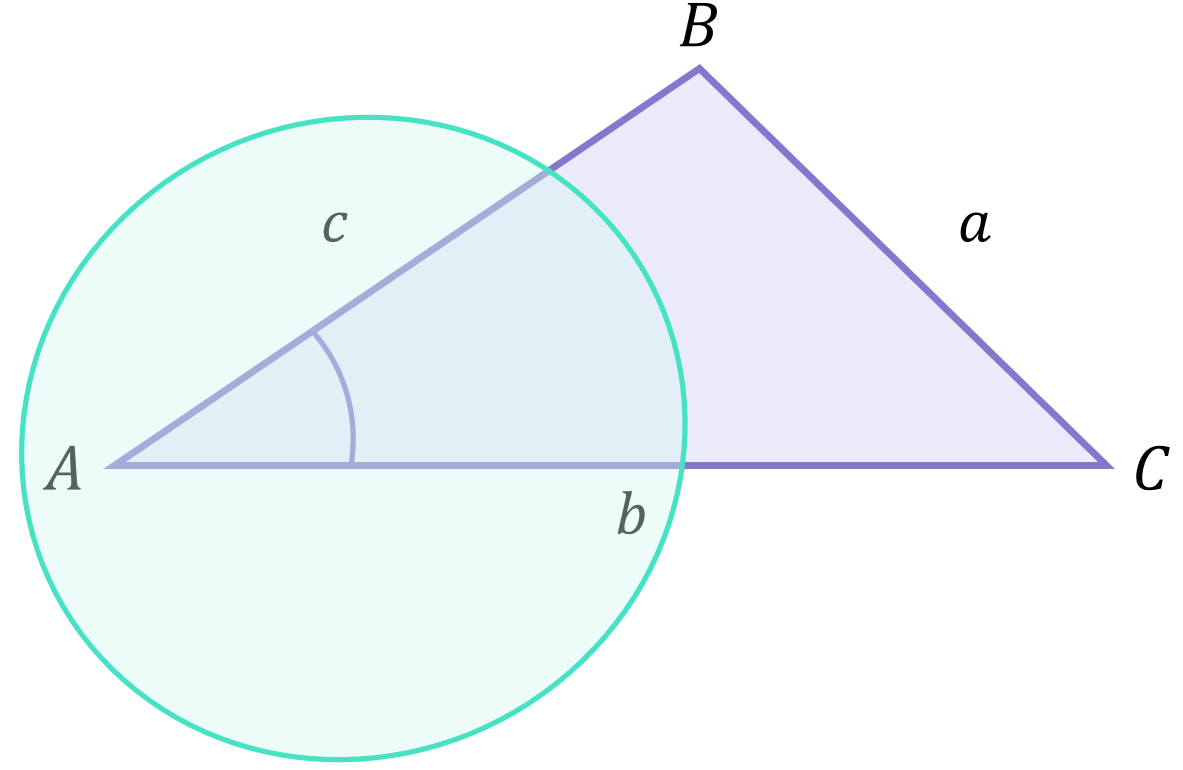
Let’s try a few examples which make use of Form 1 of the Cosine Rule.

Calculate the length of side a:

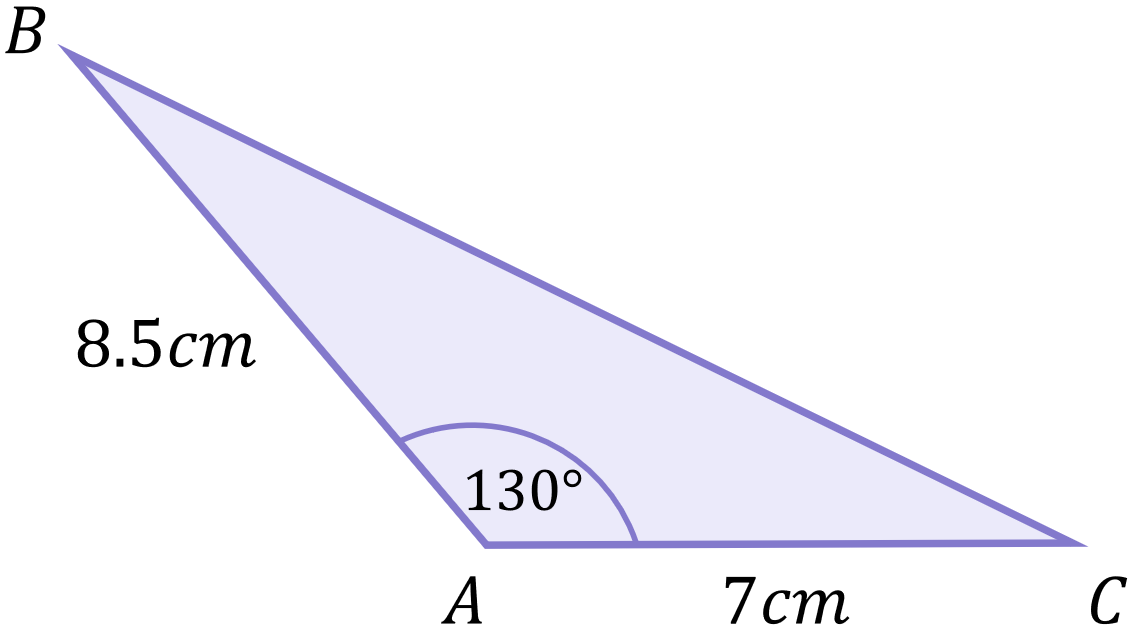
Since we know two sides plus the included angle, we can use Form 1 of the Cosine Rule:

\begin{aligned}a^{2}=b^{2}+c^{2}-2bc\cos{A}\end{aligned}

We know that b=7, c=8.5 and A=130^\circ, so we can substitute these values:

\begin{aligned}a^{2}&=(7)^{2}+(8.5)^{2}-2(7)(8.5)\cos{130} \\[12pt]a^{2}&=121.25-119\cos{130} \\[12pt]a^{2}&=121.25-119(-0.643) \\[12pt]a^{2}&=121.25+76.49 \\[12pt]a^{2}&=197.74 \\[12pt]a&=\sqrt{197.74} \\[12pt]a&=14.1cm\end{aligned}

Calculate the length of side b:

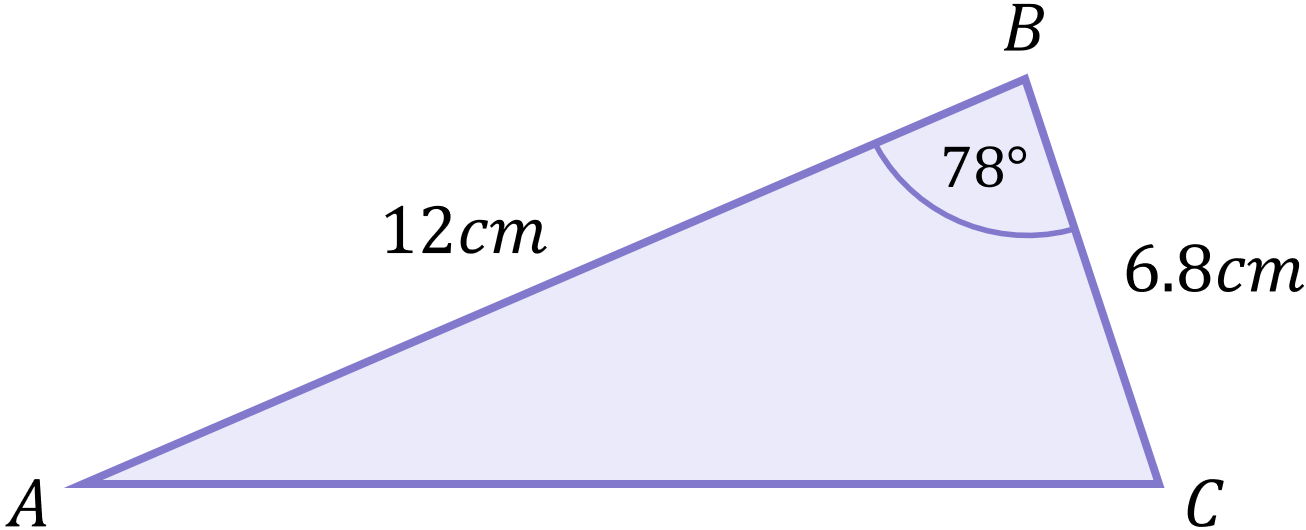
Since we know two sides plus the included angle, we can use Form 1 of the Cosine Rule (restated with side b as the subject):

\begin{aligned}b^{2}=a^{2}+c^{2}-2ac\cos{B}\end{aligned}

We know that a=6.8, c=12 and B=78^\circ, so we can substitute these values:

\begin{aligned}b^{2}&=(6.8)^{2}+(12)^{2}-2(6.8)(12)\cos{78} \\[12pt]b^{2}&=46.24+144-163.2\cos{78} \\[12pt]b^{2}&=190.24-163.2(0.208) \\[12pt]b^{2}&=190.24-33.93 \\[12pt]b^{2}&=156.31 \\[12pt]b&=\sqrt{156.31} \\[12pt]b&=12.5cm\end{aligned}

Remember, the Cosine Rule steps in where the Sine Rule fails. But the converse is also true – if you cannot use the Cosine Rule to calculate an angle or side (because you don’t have the correct set up to use either Form 1 or Form 2 of the rule) then you will have to use the Sine Rule instead. The Cosine and Sine rules are complementary in this sense.