Simultaneous equations are useful for solving equations where there are two or more unknowns you’d like to figure out. At this level you will only see equations which have two unknowns, but the technique is very powerful and can be extended to equations with any number of variables.

Let me illustrate the point. Suppose you have an equation with two unknowns – x and y:

\begin{aligned}x+y=10\end{aligned}

What are the numerical values of x and y? Without further information, this question is impossible to answer as there are infinitely many possible solutions. We could have:

\begin{aligned}x&=5\ \text{and}\ y=5          &\boldsymbol{\rightarrow}               x+y&=5+5=10  \\[12pt]x&=2\ \text{and}\ y=8          &\boldsymbol{\rightarrow}               x+y&=2+8=10 \\[12pt]x&=-5\ \text{and}\ y=15          &\boldsymbol{\rightarrow}               x+y&=-5+15=10 \\[12pt]x&=-246\ \text{and}\ y=256          &\boldsymbol{\rightarrow}               x+y&=-246+256=10\end{aligned}

These are random examples of possible values for x and y which add to 10, but you could find many more combinations I am sure. But on its own, the fact that we know x+y=10 tells us precisely nothing about x and y – we need more information!

But suppose we were also told that x+2y=17, then altogether we know:

\begin{aligned}x+y&=10 \\[12pt]x+2y&=17\end{aligned}

Using simultaneous equations, we can essentially “mash” these two equations together to eliminate one of the variables. Eliminating one of the variables means there will only be one unknown left in the equation, and you can always find a numerical answer for equations with only one unknown term.

To do this, we first label the equations as ① and ② to help us (and your examiner) keep track:

\begin{aligned}x+y&=10 - \text{①} \\[12pt]x+2y&=17 - \boldsymbol{②}\end{aligned}

Notice that ① and ② have the same quantity of x (they each have one x). If we subtract the two equations from each other, the x terms will therefore cancel out. In simultaneous equation questions, it is important to let your examiner know what actions you are taking, so make this clear at the side of your page:

Action: ② – ①

\begin{aligned}(x-x)+(2y-y)&=17-10\\[12pt]2y-y&=17-10 \\[12pt]y&=7\end{aligned}

In subtracting the equations, we have eliminated all x terms since x-x=0. On the LHS, we are left with a single y since 2y-y=y, and on the RHS we have 7 since 17-10=7. Note that it is the x terms that subtract from the other x terms, the y terms from the other y terms, and the constants (i.e. the numbers) from the other constants. In other words, the like-terms are communicating with one another (recall that like-terms stack together whereas unlike-terms do not).

Notice that if we had performed the subtraction the other way around, it would have led to exactly the same result:

Action: ① – ②

\begin{aligned}(x-x)+(y-2y)&=10-17\\[12pt]y-2y&=10-17 \\[12pt]-y&=-7 \\[12pt]y&=7\end{aligned}

The order in which you cancel the terms does not matter, but there may be a more sensible order to do it in. Generally speaking, the most sensible order will be whichever order avoids negative terms since these complicate matters unnecessarily.

So now that we know y=7, we can use this information to determine the numerical value of x. To do this, we substitute the fact that y=7 into either equation ① or ②, it does not matter which. Let’s choose equation ① for simplicity:

\begin{aligned}x+y&=10 - ① \\[12pt]x+(7)&=10 \\[12pt]x&=10-7 \\[12pt]x&=3\end{aligned}

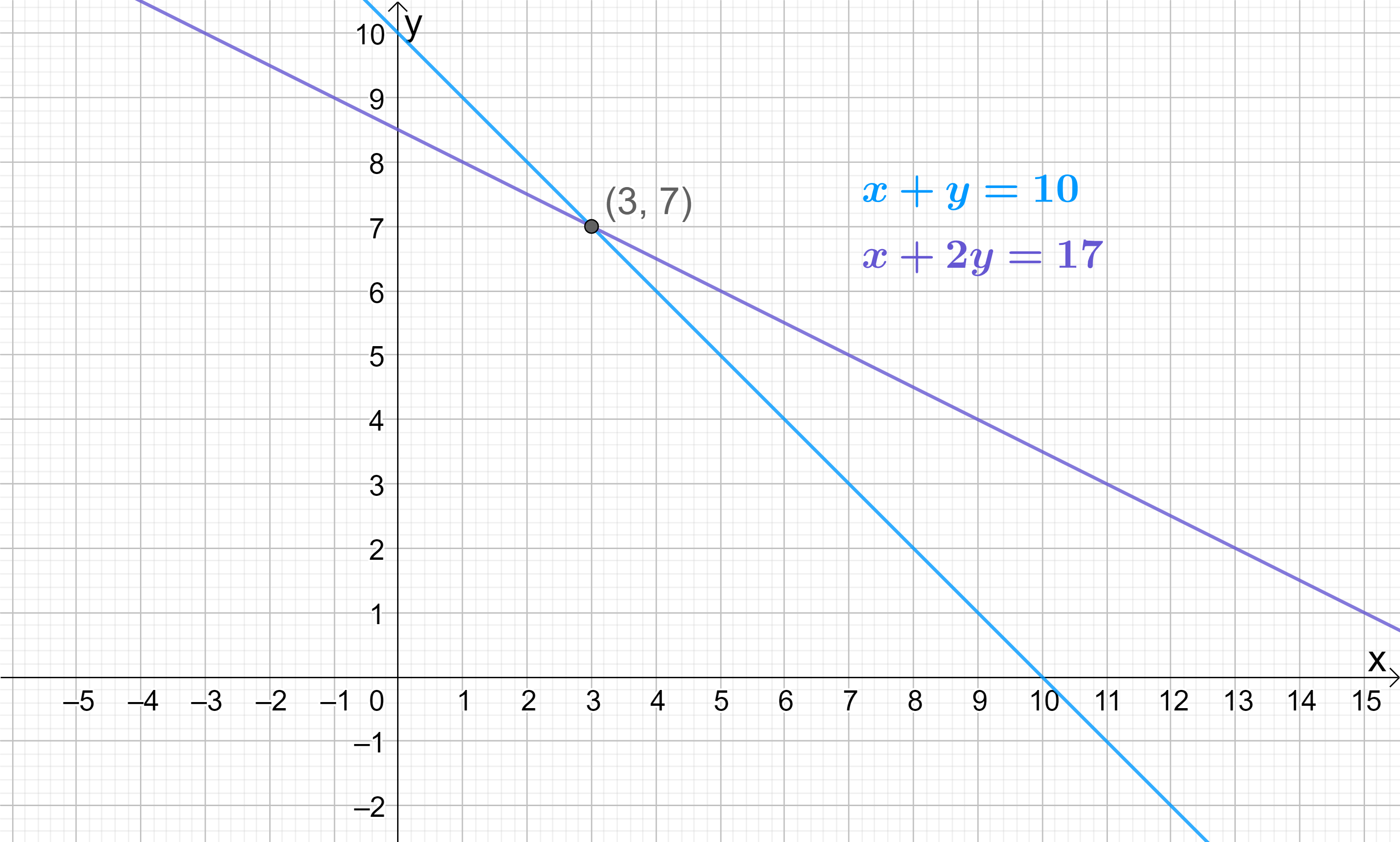
At the beginning, when we only knew that x+y=10, we said there were infinitely many possible solutions for x and y, but with the additional information that x+2y=17, we have been able to definitively prove that x=3 and y=7 by solving the equations simultaneously.

If we graph the two equations x+y=10 and x+2y=17, this gives us some added confirmation as we see that the point of intersection – the “simultaneous solution” – is indeed the coordinate (3,7) (i.e. where x=3 and y=7):

In this first example, it was fairly straightforward to eliminate one of the variables since the two equations:

\begin{aligned}x+y&=10 \\[12pt]x+2y&=17\end{aligned}

Each had the same quantity of x to begin with (they each had only one x), so subtracting them caused the x terms to cancel out immediately. However, if two equations don’t have an equivalent quantity of a variable, we must adjust the equations.

Let’s look at another example. Suppose you have:

\begin{aligned}x+y&=7 - ① \\[12pt]3x+2y&=19 - ②\end{aligned}

Adding or subtracting equations ① and ② in any order won’t cause either the x terms or the y terms to cancel out since there are different amounts of x and y in each equation. One way to get around this is to multiply equation ① through by 2 on both sides (refer to the Algebra and Rearranging Equations module for more detail on why it is ok to do this). As always with simultaneous equations questions, make it clear to your examiner what you are doing:

Action: ①\times2

\begin{aligned}2x+2y&=14 - ③ \\[12pt]3x+2y&=19 - ②\end{aligned}

Since we have made changes to equation ①, we have relabelled it as equation ③. Multiplying equation ① by 2 has resulted in the two equations now having the same quantity of y (they both now have 2y). Subtracting the two equations will now cause the y terms to cancel out:

Action: ② – ③

\begin{aligned}(3x-2x)+(2y-2y)&=19-14 \\[12pt]x&=5\end{aligned}

In subtracting the equations, we have eliminated all y terms since 2y-2y=0. On the LHS, we are left with a single x since 3x-2x=x, and on the RHS we have 5 since 19-14=5.

Now that we know x=5, we can use this information to determine the numerical value of y. Let’s substitute the fact that x=5 into equation ① for simplicity:

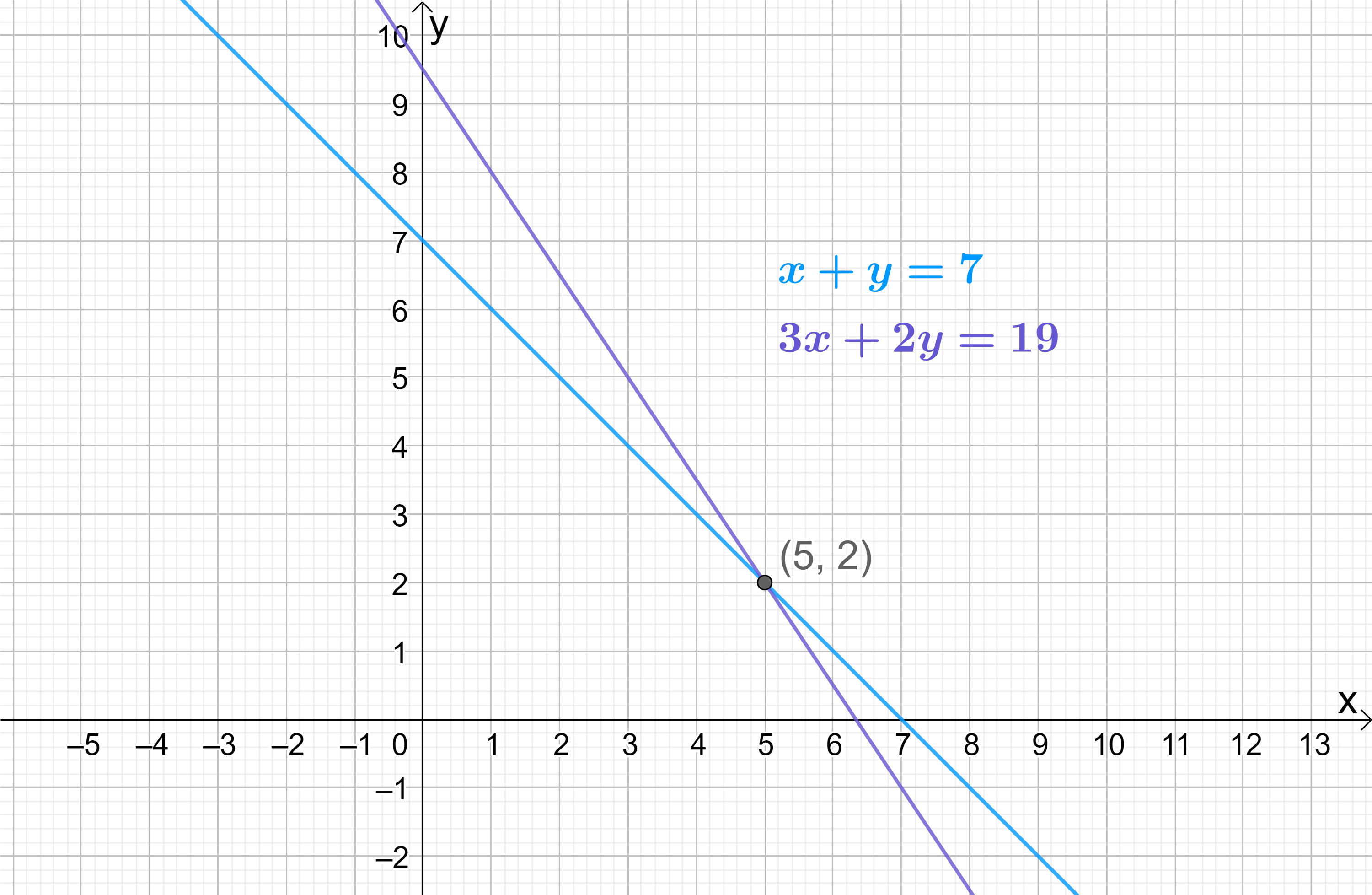
\begin{aligned}x+y&=7 - ① \\[12pt](5)+y&=7 \\[12pt]y&=7-5 \\[12pt]y&=2\end{aligned}

The point of intersection – the “simultaneous solution” – of the two lines is therefore the coordinate (5,2) (i.e. where x=5 and y=2). Once again, graphing the two lines confirms this:

In the examples so far, all the lines have been of the same form with the x and y terms on the LHS and the constant on the RHS. To complicate matters, it’s quite possible your examiners wouldn’t give you lines in the same format to start with, requiring you to rearrange the lines first. That’s ok – nothing we can’t handle!

Such an example may look like this:

\begin{aligned}4x+y&=9 - ① \\[12pt]6&=4y-6x+3 - ②\end{aligned}

You can see straight away that these lines are not in the same form. In this case, it is easiest to rearrange equation ② into the typical form for these questions (x and y terms on the LHS, constant on the RHS). Doing this, we find:

\begin{aligned}4x+y&=9 - ① \\[12pt]6x-4y&=-3 - ②\end{aligned}

I have not relabelled equation ② since we have not adjusted the equation (by multiplying it for example), we have only rearranged it.

Adding or subtracting equations ① and ② in their current forms won’t cause either the x terms or the y terms to cancel out since there are different amounts of x and y in each equation. One way to get around this is to multiply equation ① through by 4 on both sides. Doing this gives:

Action: ①\times4

\begin{aligned}16x+4y&=36 - ③ \\[12pt]6x-4y&=-3 - ②\end{aligned}

Since we have now made changes to equation ①, we have relabelled it as equation ③. Multiplying equation ① by 4 has resulted in the two equations now having equal but opposite quantities of y (i.e. they both have four y terms, but one is positive while the other is negative). Adding the two equations will now cause the y terms to cancel out:

Action: ②+③

\begin{aligned}(6x+16x)+(-4y+4y)&=-3+36 \\[12pt]22x&=33 \\[12pt]x&=\frac{33}{22} \\[12pt]x&=\frac{3\times\sout{11}}{2\times\sout{11}} \\[12pt]x&=\frac{3}{2}\end{aligned}

Now that we know x=\frac{3}{2}, let’s substitute this into equation ①:

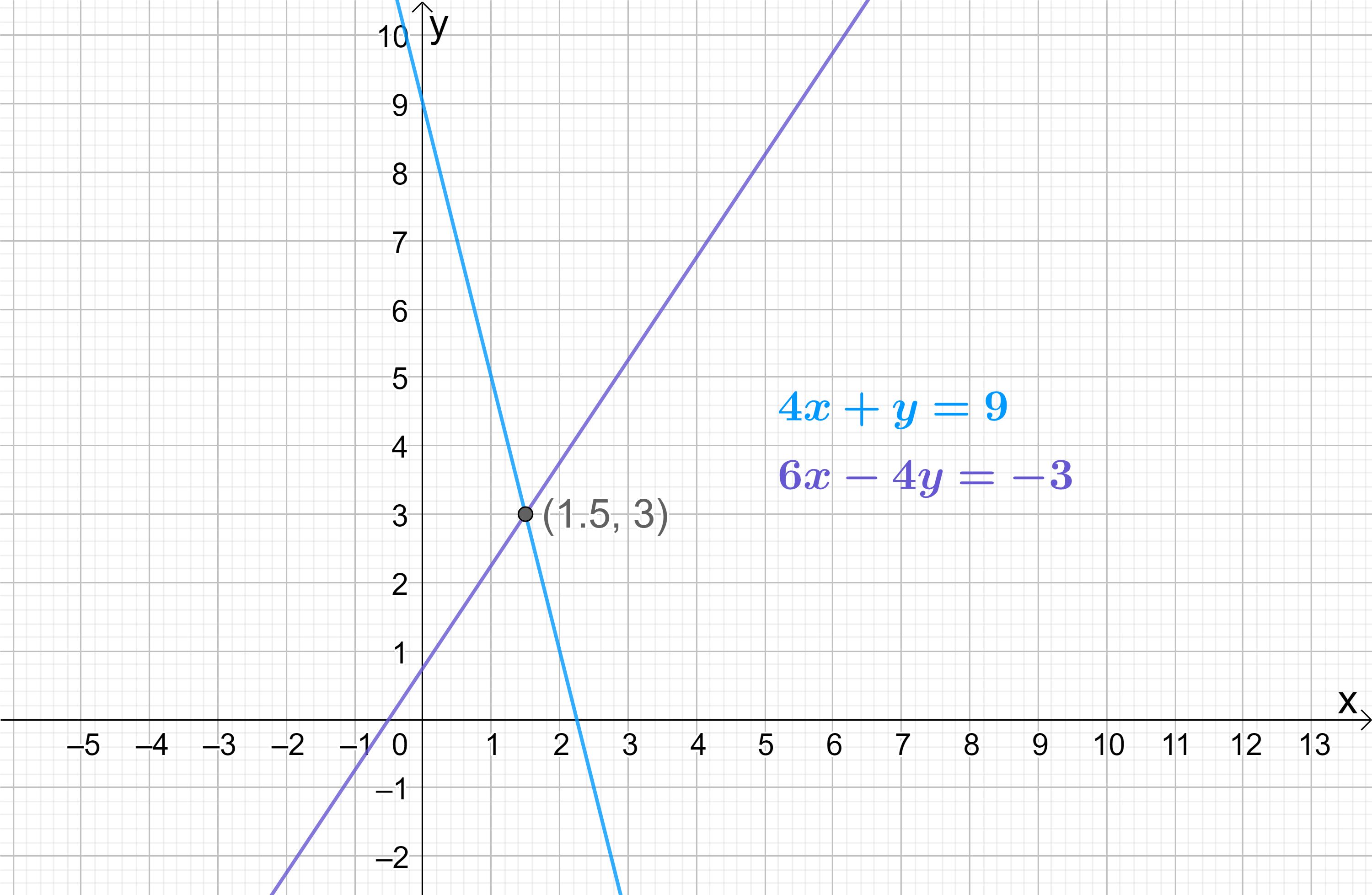
\begin{aligned}4x+y&=9 - ① \\[10pt]4\left(\frac{3}{2}\right)+y&=9 \\[14pt]6+y&=9 \\[14pt]y&=3\end{aligned}

The point of intersection – the “simultaneous solution” – of the two lines is therefore the coordinate (\frac{3}{2},3) (i.e. where x=\frac{3}{2} and y=3). For the final time, let’s confirm this is true graphically: