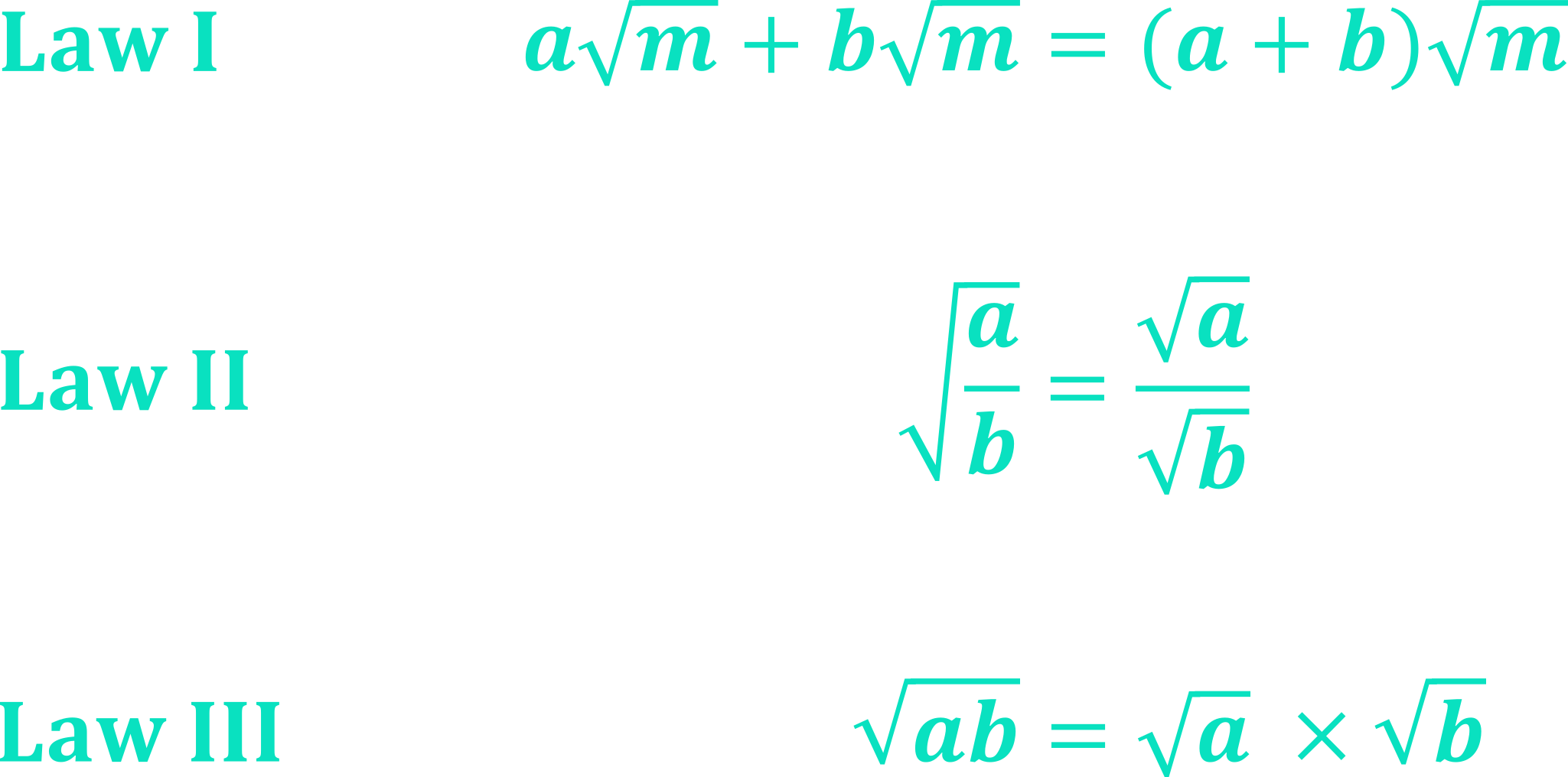The Laws of Surds define how we manipulate and simplify surds, so knowing these enables you to tackle any algebraic situation involving surds. Fortunately, there are only three Laws of Surds to know and they are fairly straightforward:

Let’s examine each Law in turn to understand it in more detail.

Law I states that like-surds stack up (recall the key principle that all like-terms add together, or “stack up”). \sqrt{m} just stands for some random surd: it could be \sqrt{3}, \sqrt{5}, \sqrt{10}, or any other surd, it does not matter. a and b are just multiplying factors, or “amounts” of that surd, which could be any number. As an example, let’s suppose:

\begin{aligned}a&=2 \\[12pt]b&=5 \\[12pt]\sqrt m&=\sqrt3\end{aligned}

Then we would have:

\begin{aligned}a\sqrt{m}+b\sqrt{m}&=(a+b)\sqrt{m} \\[12pt]2\sqrt{3}+5\sqrt{3}&=(2+5)\sqrt{3}=7\sqrt{3}\end{aligned}

This is actually pretty obvious isn’t it? 2 of anything, plus 5 of that same thing, is 7 of that thing. 2 elephants plus 5 elephants are 7 elephants. So, 2 \sqrt{3}’s, plus 5 \sqrt{3}’s, must be 7 \sqrt{3}’s. We’re just adding different quantities of \sqrt{3} and these stack up together since \sqrt{3}’s are like-terms.

It is important to note that we cannot apply Law I when the surds are not like-terms. Take the following problem:

\begin{aligned}\sqrt3+\sqrt2\end{aligned}

You can add an apple and an apple because they are like-terms, and you get two apples.
You cannot add an apple and an orange, because they are not like-terms.

By essentially the same logic:

You can add \sqrt3 and \sqrt3 because they are like-terms, and you get 2\sqrt3.
You cannot add \sqrt3 and \sqrt2 because they are not like-terms.

Law II states that the root of a fraction can be written as a fraction of separate roots. As an example, let’s suppose:

\begin{aligned}a&=16 \\[12pt]b&=25\end{aligned}

Then we have:

\begin{aligned}\sqrt{\frac{a}{b}}=\sqrt{\frac{16}{25}}\end{aligned}

If we did not have Law II, to approach this question we’d first have to figure out \frac{16}{25} as a decimal, which we could do with long division:

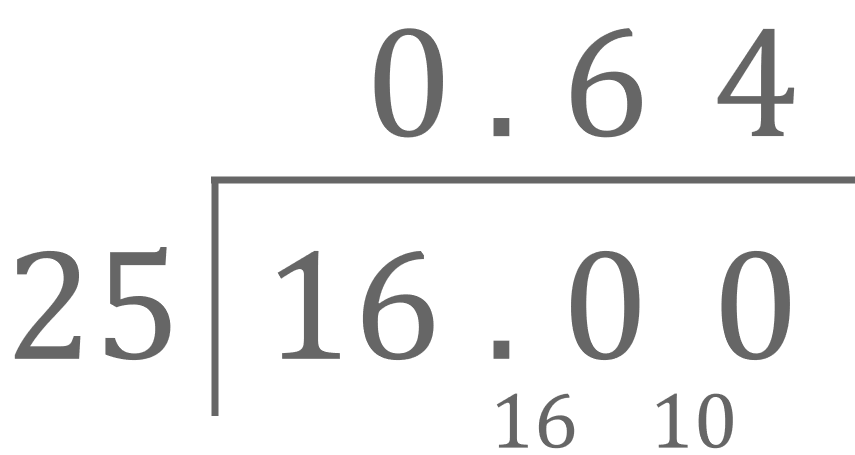
Thus we have:

\begin{aligned}\sqrt{\frac{16}{25}}=\sqrt{0.64}\end{aligned}

The square root of 64 is 8, so the square root of 0.64 = 0.8 (check that 0.8 x 0.8 = 0.64 in your calculator). So, altogether we have:

\begin{aligned}\sqrt{\frac{a}{b}}=\sqrt{\frac{16}{25}}=\sqrt{0.64}=0.8\end{aligned}

This is manageable, but it is quite a task to work all of this out without a calculator. So if \sqrt{\frac{16}{25}} came up in your non-calculator paper, we would use the Laws of Surds to make this easier. Using Law II, we can write:

\begin{aligned}\sqrt{\frac{16}{25}}=\frac{\sqrt{16}}{\sqrt{25}}\end{aligned}

This is much easier to work with since the individual roots are ones we are very familiar with:

\begin{aligned}&=\frac{\sqrt{16}}{\sqrt{25}} \\[12pt]&=\frac{4}{5} \\[12pt]&=0.8\end{aligned}

Employing Law II made the calculation far simpler and returned exactly the same result as before.

Law III states that products of surds (\boldsymbol{\sqrt{a}\times\sqrt{b}}) can be combined into a single surd (\boldsymbol{\sqrt{ab}}). This also works the other way around – single surds can be split up into products of two surds. Law III is probably the most important Law to you right now as it is likely to feature in your exams and schoolwork more prominently than the other Laws.

At this level, Law III is mostly used in surd simplification questions. As an example, let’s suppose we had to simplify \sqrt{20}. Instead of thinking of 20 as just 20, if we consider 20 as a product by writing 20=4\times 5 then we are able to utilise Law III to write:

\begin{aligned}\sqrt{20}&=\sqrt{4\times 5} \\[12pt]&=\sqrt4\times \sqrt5\ \\[12pt]&=2\times \sqrt5 \\[12pt]&=2\sqrt5\end{aligned}

We have now simplified the surd. Just as with fractions, you should always simplify a surd if it is possible to do so.

We could have split \sqrt{20} into a different product as follows:

\begin{aligned}\sqrt{20}&=\sqrt{2\times 10} \\[12pt]&=\sqrt2\times \sqrt{10}\end{aligned}

Splitting \sqrt{20} in this way is not a good idea – it leaves us with nowhere to go since \sqrt2 and \sqrt{10} are surds which cannot be further simplified. When we split \sqrt{20} into \sqrt4 and \sqrt5, since \sqrt4 was a square number with an exact decimal square root (i.e. \sqrt4=2) then we were able to go one step further with our simplification.

Therefore, when simplifying any surd using Law III you need to find the highest square factor of the surd (in other words, you need to check whether 1, 4, 9, 16, 25, 36, 49, etc… are factors of the surd).

In the case of \sqrt{20}, the highest square factor (i.e. the highest square number that fits perfectly into 20) was 4. The arithmetic can be a little more challenging with larger numbers, but the process is exactly the same.

Taking a slightly more complicated example, simplifying \sqrt{80} can be done as follows:

\begin{aligned}&\text{Option 1:}               &               &\text{Option 2:} \\[12pt]&\sqrt{80}=\sqrt{4}\times\sqrt{20}              &               &\sqrt{80}=\sqrt{16}\times\sqrt{5} \\[12pt]&\sqrt{80}=2\times(\sqrt{4}\times\sqrt{5})              &               &\sqrt{80}=4\times\sqrt{5} \\[12pt]&\sqrt{80}=2\times(2\times\sqrt{5})              &               &\sqrt{80}=4\sqrt{5} \\[12pt]&\sqrt{80}=2\times2\sqrt{5}              &               & \\[12pt]&\sqrt{80}=4\sqrt{5}              &               &\end{aligned}

While both options lead to the same final simplified form, it is clear that Option 2 is the better one since it involves less working. In both options, \sqrt{80} has been factorised using square numbers: both 4 and 16 are square numbers that fit perfectly into 80. However, 16 is the highest square factor of 80, and using the highest square factor will always bring you to the final answer faster. Option 1 is entirely correct and there is nothing wrong with simplifying \sqrt{80} in this way – it is just a bit less efficient than Option 2!

One very common way examiners like to challenge your knowledge of simplifying surds is through “rationalising the denominator” questions. You have no doubt heard this phrase before and possibly wondered what it actually means… The below examples should help shed some light on this!

Rationalise the denominator of \frac{2}{\sqrt{7}}

This is a very common question type in exams, and the good news is it’s actually really simple to do once you know how! 

We have been asked to “rationalise” the denominator of \frac{2}{\sqrt7} – but what does this even mean?

The denominator is currently \sqrt7. This is a surd, and like all surds, it belongs to the set of Real Numbers. Surds do not belong to the set of Rational Numbers. By asking us to “rationalise” the denominator, an examiner wants us to change the denominator to a number that does belong to the set of Rational Numbers.

But of course, we cannot simply swap the denominator for any old number that belongs to the set of Rational Numbers – that would change the overall value of the fraction, which makes no sense. That would be like randomly changing the denominator of \frac{1}{2} (which has a value of 0.5) to have a denominator of 4, i.e. \frac{1}{4} (which has a value of 0.25) – clearly you can’t just do that!

So, we have to somehow change the denominator to a number that belongs to the Rational Numbers but without changing the overall value of the fraction.

To do this, recall the very useful rule:

If we apply this cleverly, we can rationalise the denominator as follows:

\begin{aligned}&\ \ \ \ \ \ \frac{2}{\sqrt7} \\[12pt]&=\frac{2}{\sqrt7}\times \frac{\sqrt7}{\sqrt7}\end{aligned}

Multiplying by \frac{\sqrt7}{\sqrt7} is perfectly acceptable since \frac{\sqrt7}{\sqrt7}=1, and multiplying by 1 doesn’t change the value of a term. Anything multiplied by 1 is just itself.

\frac{\sqrt7}{\sqrt7} was chosen since this will cause the surd in the denominator to cease being a surd and become a rational number:

\begin{aligned}&=\frac{2}{\sqrt7}\times \frac{\sqrt7}{\sqrt7} \\[12pt]&=\frac{2\sqrt7}{\sqrt7\times \sqrt7} \\[12pt]&=\frac{2\sqrt7}{\sqrt{49}} \\[12pt]&=\frac{2\sqrt7}{7}\end{aligned}

We have now successfully rationalised the denominator since 7 belongs to the set of Rational Numbers.

We began with \frac{2}{\sqrt7} and ended with \frac{2\sqrt7}{7} – but are these fractions actually the same? You can easily check by sticking them into your calculator and getting a decimal approximation:

\begin{aligned}\frac{2}{\sqrt7}&=0.7559 \\[12pt]\frac{2\sqrt7}{7}&=0.7559\end{aligned}

As you can see, whilst these fractions may look different, they both represent the same underlying value!

This may seem like a long and complicated question, but it really isn’t. In the next example, I won’t provide any background explanation and you’ll see just how short and simple the process of rationalising a denominator actually is!

Rationalise the denominator of \frac{6}{\sqrt{27}}

First, simplify the surd – remember, you should always simplify a surd if it is possible to do so:

\begin{aligned}&\ \ \ \ \ \ \frac{6}{\sqrt{27}} \\[12pt]&=\frac{6}{\sqrt9\times\sqrt3} \\[12pt]&=\frac{6}{3\sqrt3} \\[12pt]&=\frac{2}{\sqrt3}\end{aligned}

Now, we rationalise the denominator using the same technique as before:

\begin{aligned}&\ \ \ \ \ \frac{2}{\sqrt3} \\[12pt]&=\frac{2}{\sqrt3}\times \frac{\sqrt3}{\sqrt3}\ \\[12pt]&=\frac{2\sqrt3}{\sqrt3\times\sqrt3} \\[12pt]&=\frac{2\sqrt3}{3}\end{aligned}

We have now successfully rationalised the denominator since 3 belongs to the set of Rational Numbers.