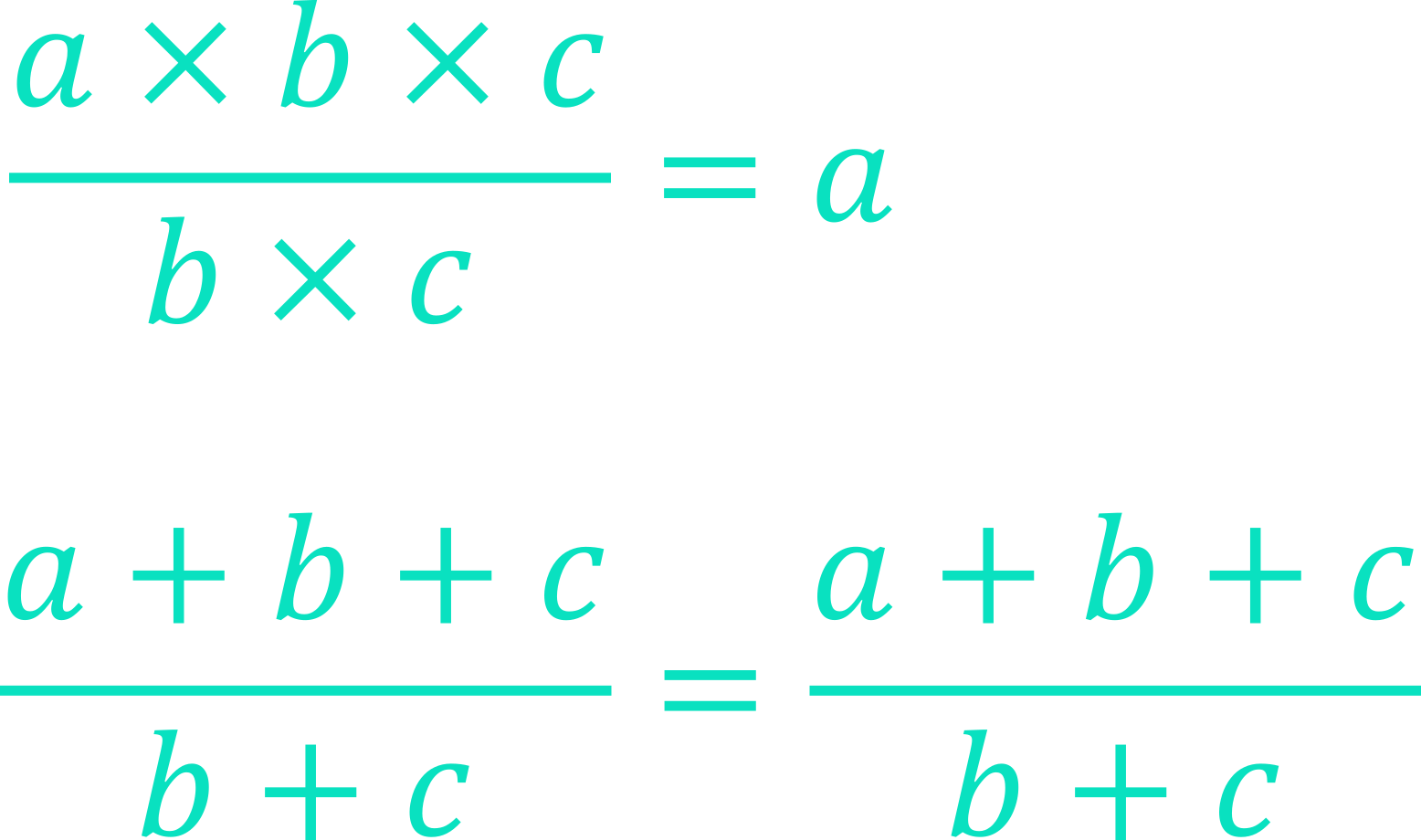There is a lot of confusion over when it is ok, and when it is not ok, to cancel out terms in an algebraic expression. Take the expression:

\begin{aligned}\frac{x+5}{5}\end{aligned}

As there is a 5 on both the numerator and the denominator, do you think it is ok to cancel out the 5s and simplify down to just x? (Hint: it’s not!)

Let’s explore when it is, and when it isn’t, appropriate to cancel out terms in more detail. Take the following two expressions where I have assumed that all the like-terms cancel each other out (recall that, in algebra, like-terms are terms that have the same variables and powers):

Expression 1

\begin{aligned}\frac{abc}{bc}=a\end{aligned}

Expression 2

\begin{aligned}\frac{a+b+c}{b+c}=\ a\end{aligned}

Now pick some values for the variables (any values will work). I will keep it simple and choose a = 2, b = 3 and c = 4. Substituting these values into the two expressions above, we find:

Expression 1

\begin{aligned}\frac{(2)(3)(4)}{(3)(4)}=\frac{24}{12}=2=a\end{aligned}

Expression 2

\begin{aligned}\frac{2+3+4}{3+4}=\frac{9}{7}\neq2=a\end{aligned}

(note that \neq means “not equal to”)

As you can see, our initial assumption that the like-terms (the b ’s and the c ’s) cancel each other out was true for Expression 1, but not Expression 2. The difference is, Expression 1 is a product (an expression where all terms are either being multiplied or divided), whereas Expression 2 is a sum (an expression where all terms are either being added or subtracted).

This simple proof shows that you can only cancel out like-terms if they are part of a product. If they are part of a sum, it is mathematically incorrect to cancel them out or simplify them down. We can summarise these conclusions in more mathematical language as follows:

\begin{aligned}\frac{abc}{bc}=a\end{aligned}

(i.e. like-terms cancel out when they are part of a product)

\begin{aligned}\frac{a+b+c}{b+c}\neq\ a\end{aligned}

(i.e. like-terms do not cancel out when they are part of a sum)

You can test the above with any values of a , b and c you can think of and the result will always be the same (try it for yourself).

It may not have occurred to you before, but when simplifying basic fractions, as you will have done countless times, you are actually making use of this rule. Take the following case:

\begin{aligned}x=\frac{18}{12}=\frac{3}{2}\end{aligned}

You know that both 18 and 12 have a common factor of 6, so you immediately simplify the faction down to \large\frac{3}{2}. This time, I will show an intermediate step:

\begin{aligned}x=\frac{18}{12}=\frac{\sout6\ \times\ 3}{\sout6\ \times\ 2}=\frac{3}{2}\end{aligned}

Here, we explicitly show that 18 can be written as 6 x 3, and 12 as 6 x 2, thus turning both the standalone numbers into products. As we have just established, it is appropriate to cancel out like-terms if they are parts of products, so we know it is correct to cancel out the 6’s, which reduces the fraction to \large\frac{3}{2} as before. There is no need to show this intermediate step as part of your working when simplifying fractions in general, but I include it here to emphasise the rule for cancellation.