Segments (And Other Circle Facts)
Of all the standard 2-D shapes we work with at National 5 level, the circle is the only one with curved edges. This affects the geometry of the shape quite considerably and gives circles some unique characteristics.
It is useful to recall the definitions of various aspects of a circle’s geometry:
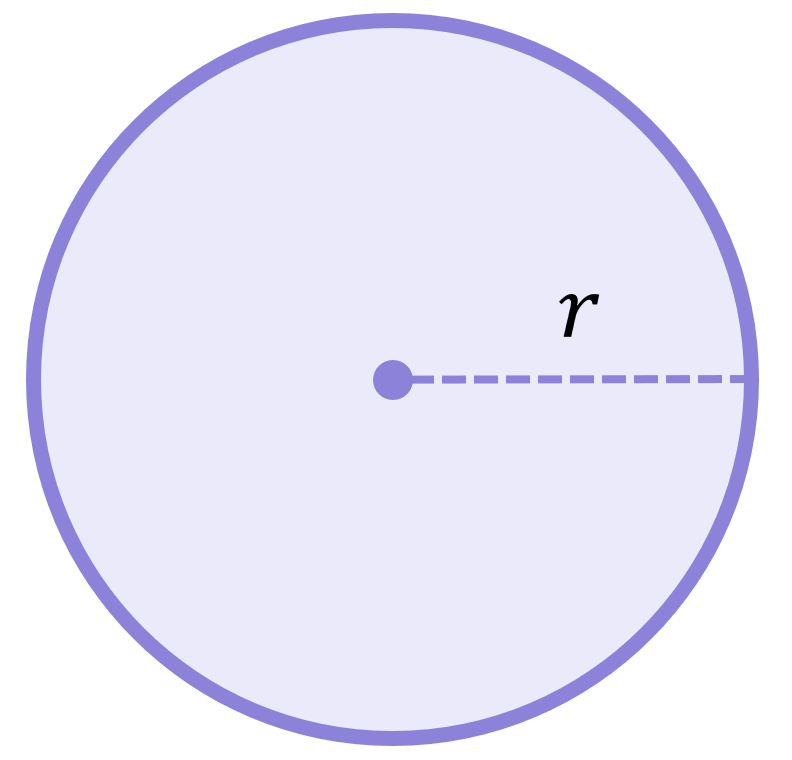
The radius is any straight line going from the centre of a circle to any point on its circumference:
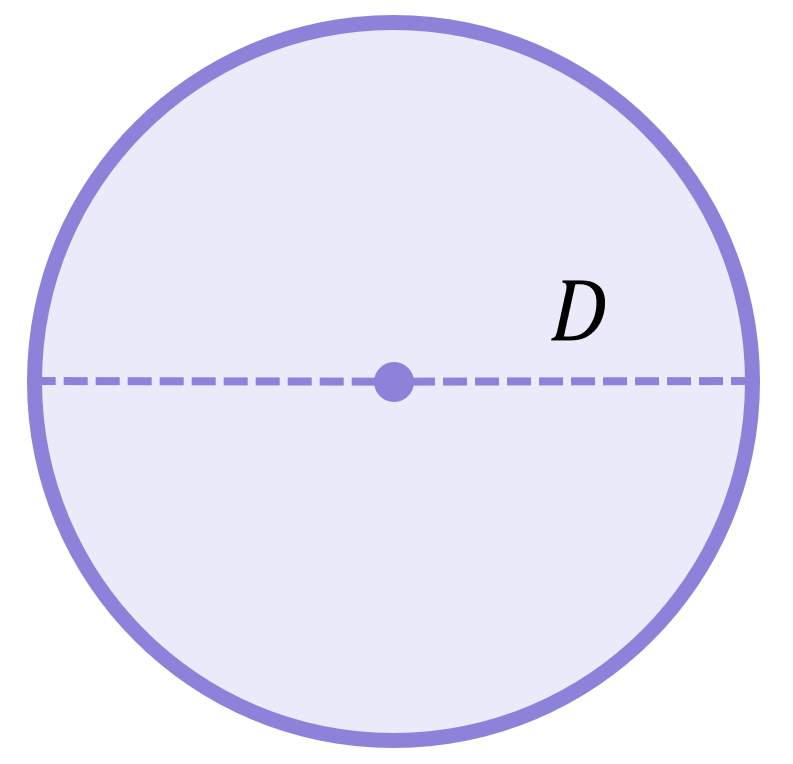
The diameter is any straight line passing through the centre of a circle whose ends both touch the circle’s circumference. A circle’s diameter is always double the length of its radius:
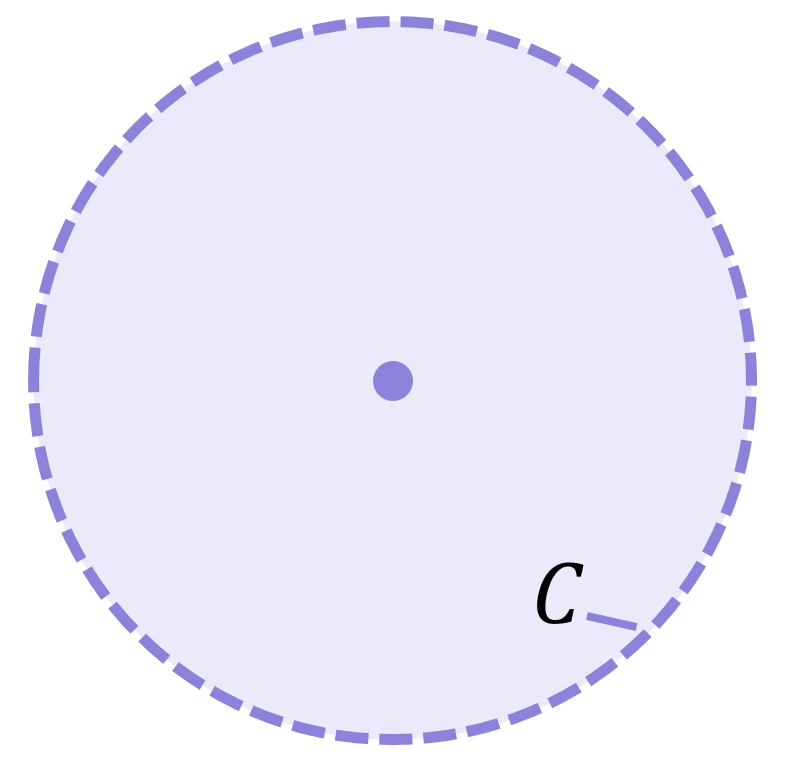
The circumference is the distance around the edge of a circle (in non-curved shapes, this is called the perimeter):
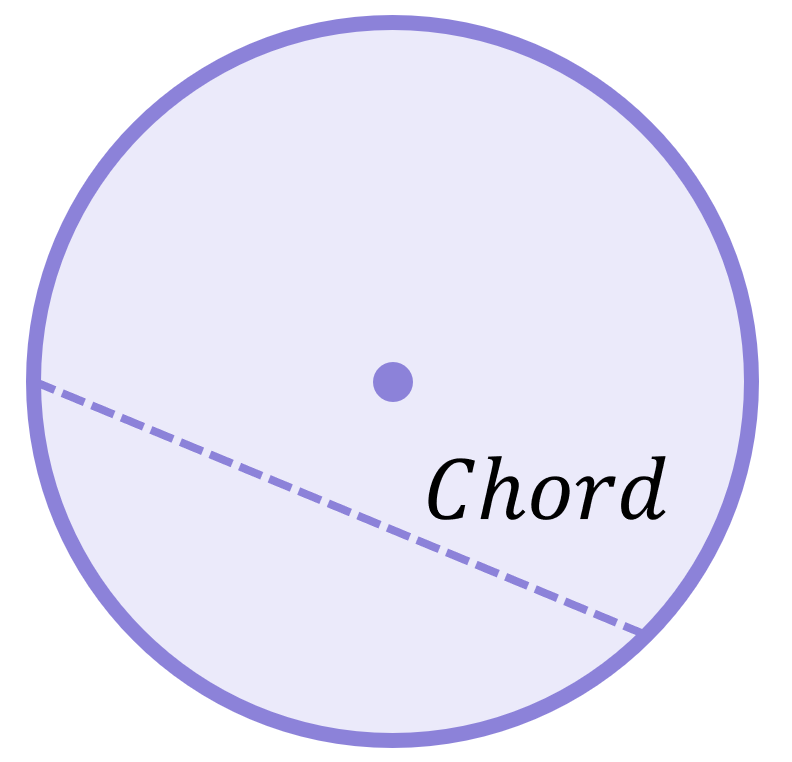
A chord is any line connecting two points on a circle’s circumference that does not pass through the centre of the circle. If the line passed through the centre, it would be a diameter (i.e. the diameter is a special chord):
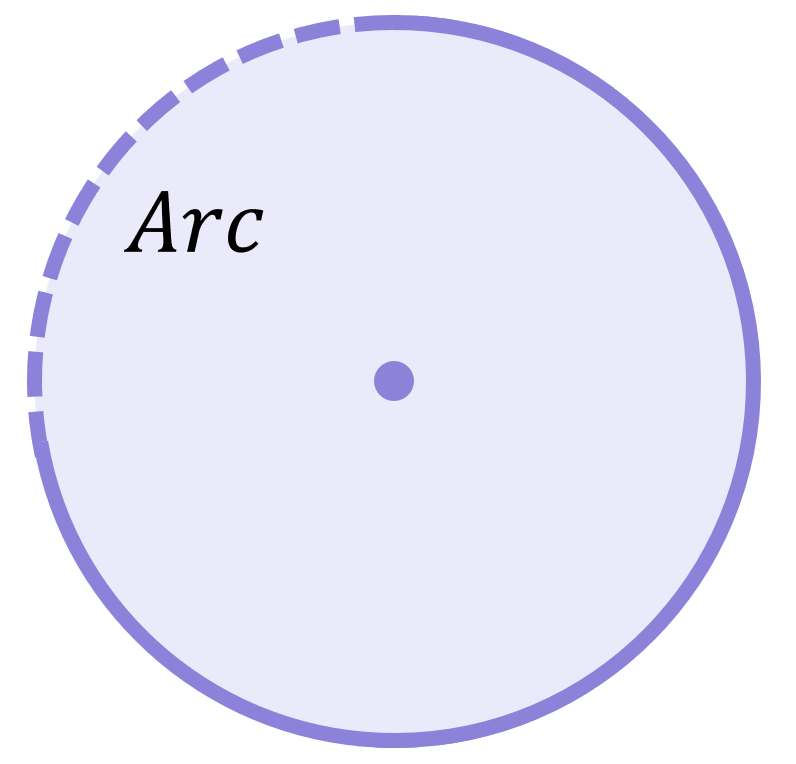
An arc is any small section of the circumference of a circle:
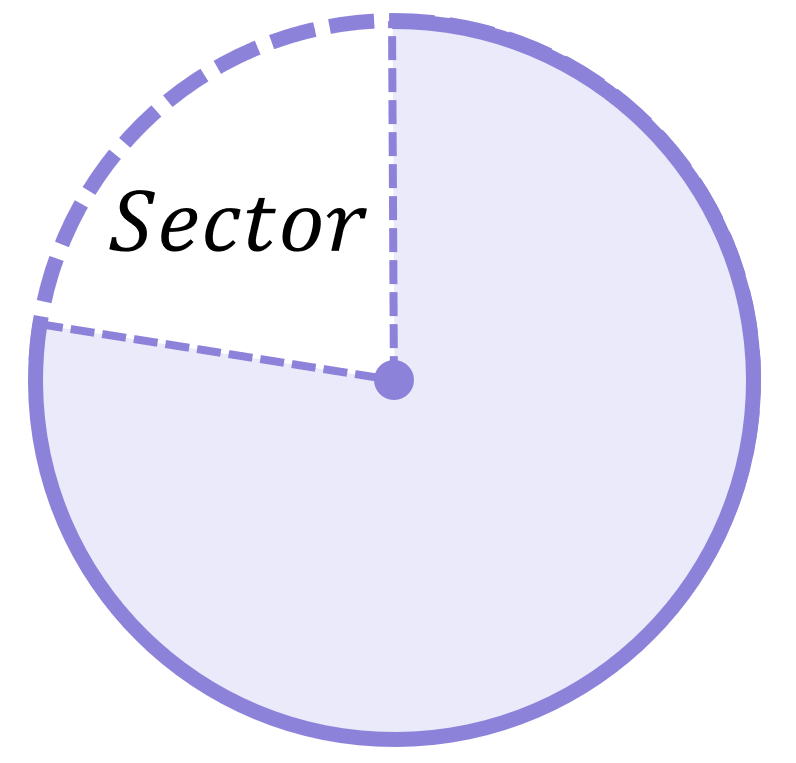
A sector is the region bounded by two radii and an arc. It is small section of the circle’s overall area. For simplicity, you can think of this as a “pizza slice” shape:
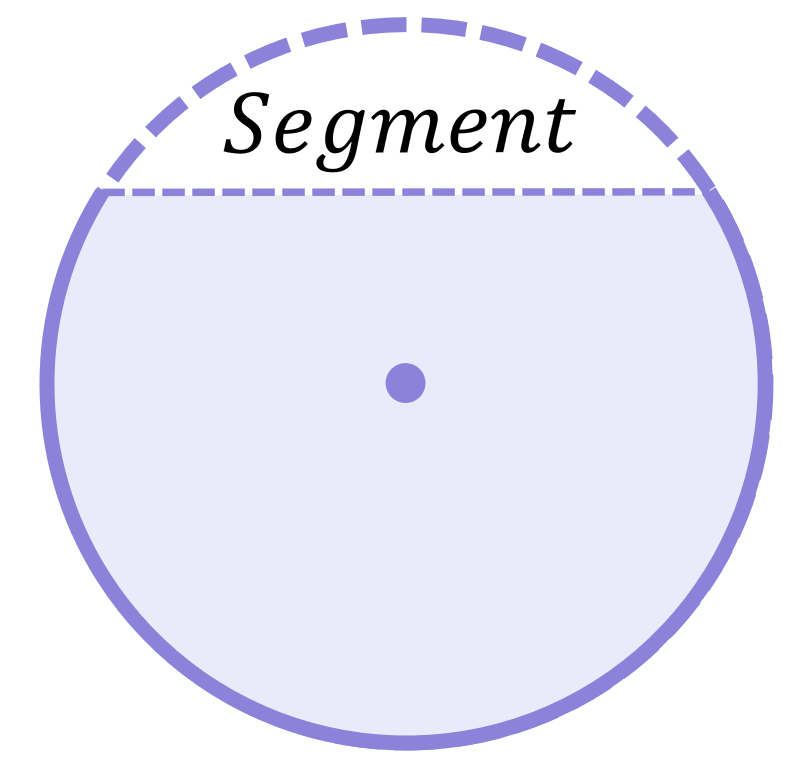
A segment is the region bounded by a chord and an arc:
Expanding on this, there are three laws of circle geometry (pertaining to angles) that you should be aware of.
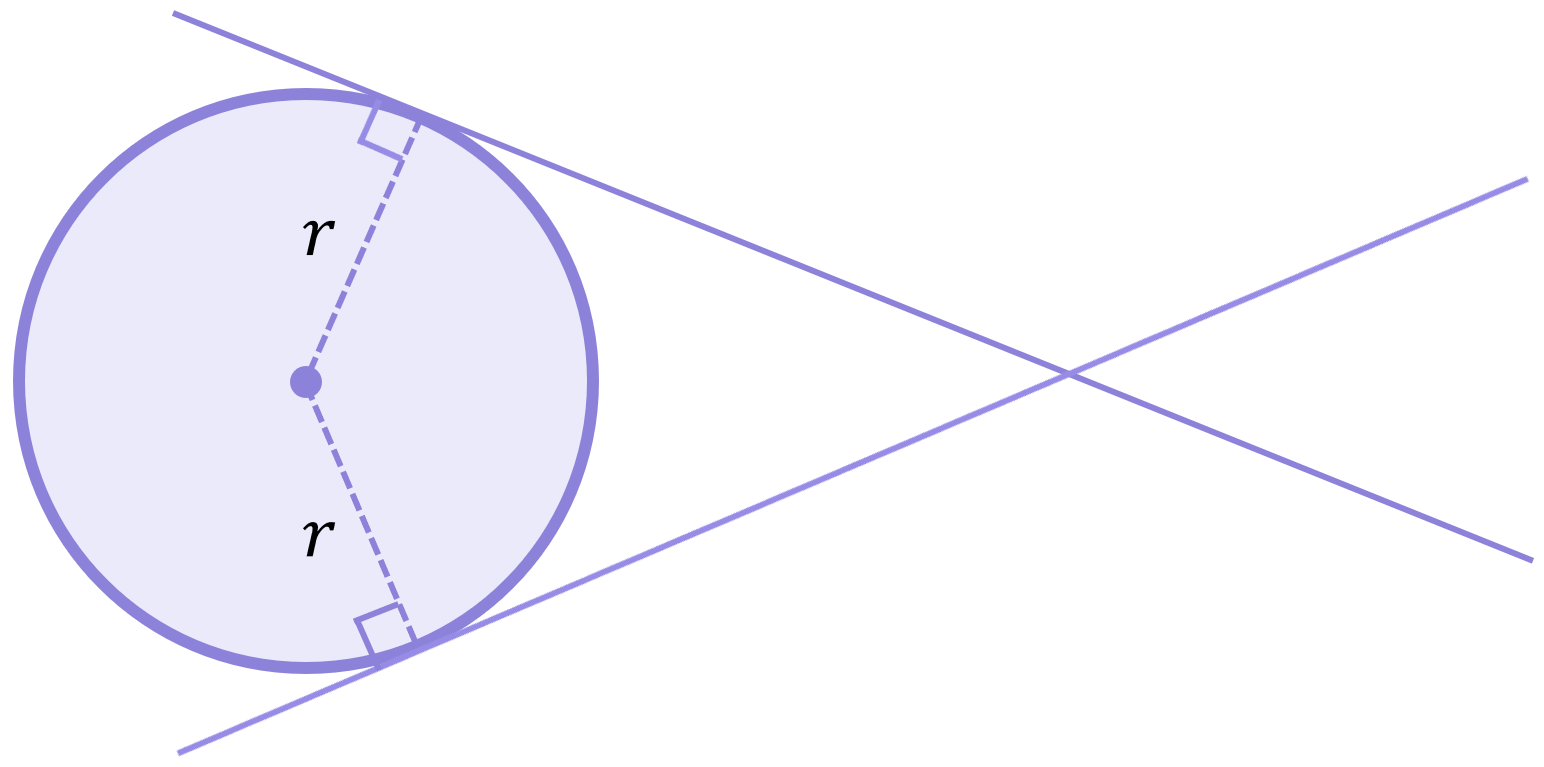
Firstly, a tangent to a curve at a given point is a straight line which “just touches” the curve at that point and no more. In circle geometry, tangents always meet radii at 90^\circ angles:
Secondly, the perpendicular bisector of any chord always passes through the centre of a circle:
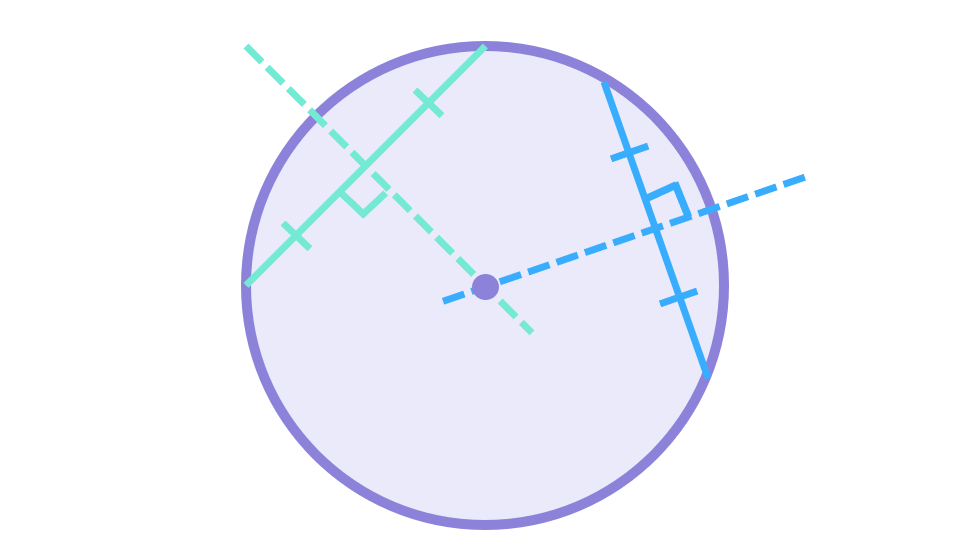
In the diagram above I have shown two possible chords (one in green and one in blue). The perpendicular bisectors of these chords are then shown as dotted lines, and it’s clear that both of these lines pass through the centre of the circle. To be clear, the perpendicular bisector of a chord is the line which passes through the chord at a 90^\circ angle such that it cuts the chord perfectly in half. These are only two of infinitely many possible chords and perpendicular bisectors I could have shown – try drawing a perpendicular bisector of a chord for yourself and you will see that it passes through the centre of the circle.
Finally, any two chords that start at opposite ends of a circle’s diameter will always meet at a 90^\circ angle:
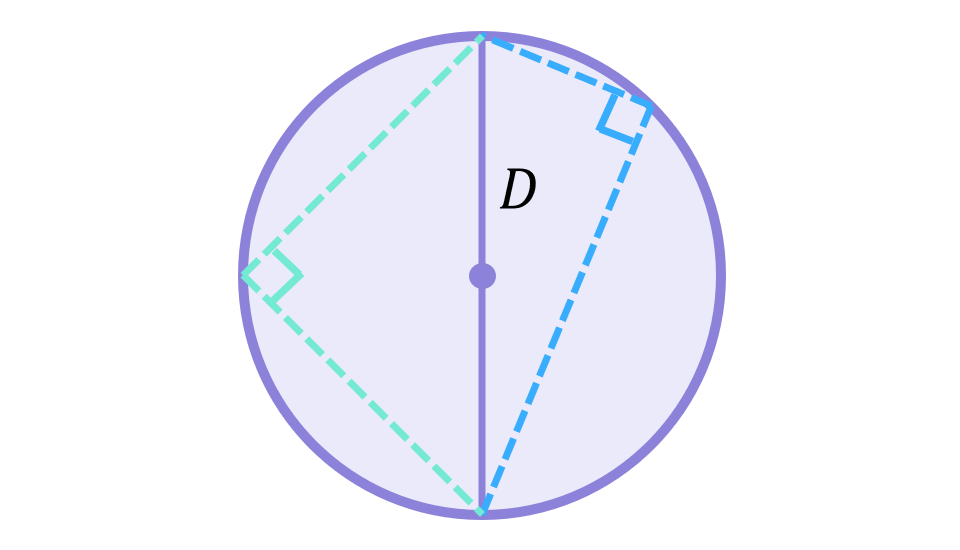
In the diagram above I have shown two possible pairs of chords that start at opposite ends of the diameter (one pair in green and the other in blue), and it is clear they meet at a 90^\circ angle. These are only two of infinitely many possible combinations of chords I could have shown – try drawing two for yourself and you’ll see they always meet at a 90^\circ angle.






