Parallel Lines
The main area you are likely to encounter parallel lines within the National 5 course is in the context of simultaneous equations.
As you now know, simultaneous equations are an algebraic method to find the point of intersection of two lines. We often call the point of intersection the “simultaneous solution”. So if the simultaneous solution is the point of intersection of the two lines, then it follows that if two lines do not intersect, then it will not be possible to solve them simultaneously.
Take for example the lines:
\begin{aligned}2x-y&=-1&- ① \\[12pt]2x-y&=2&- ②\end{aligned}
If we sketch these lines, it is immediately clear that they do not intersect:
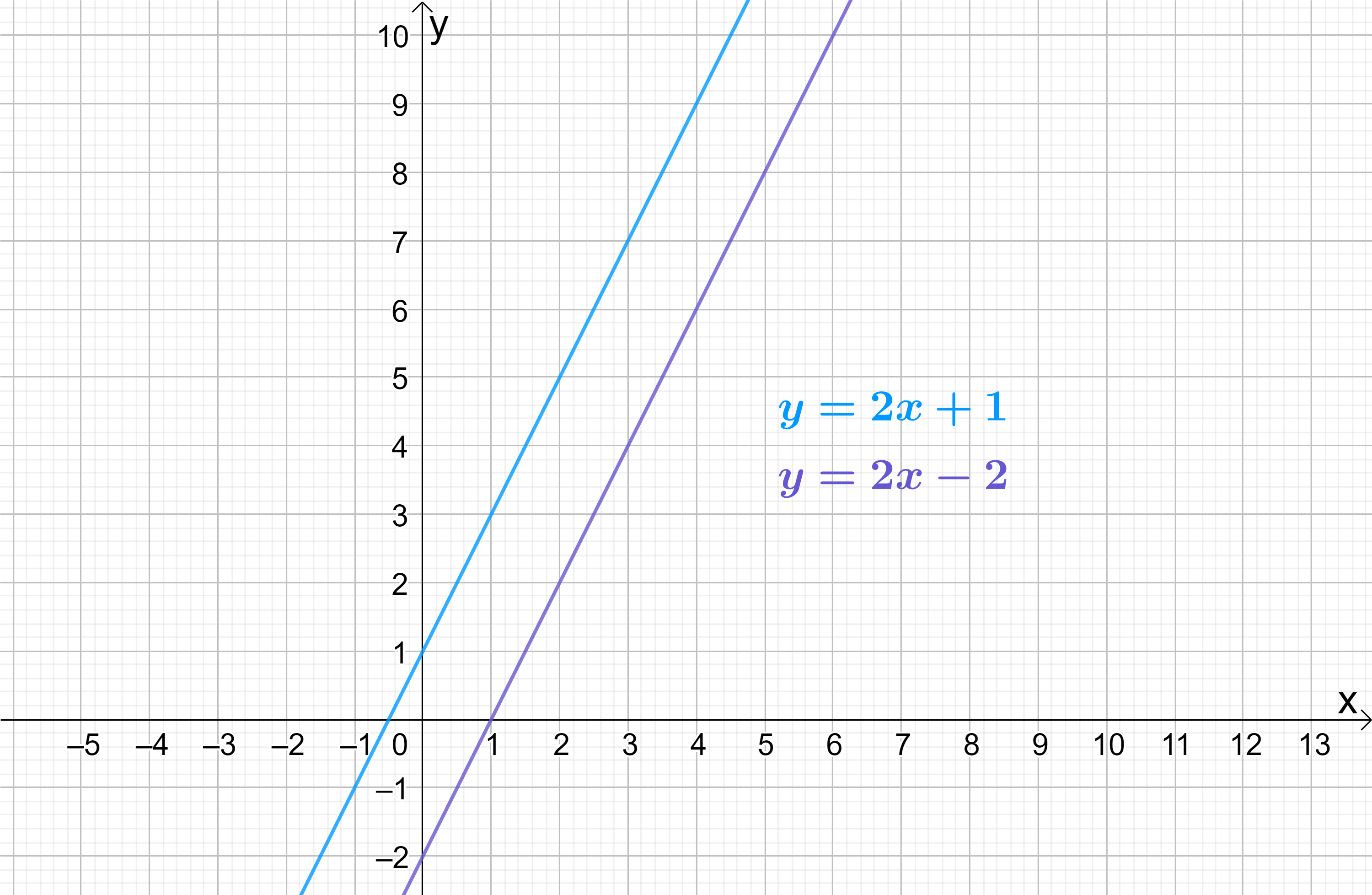
Rearranging both equations into the standard form of the General Equation y=mx+c:
\begin{aligned}y&=2x+1 - ① \\[12pt]y&=2x-2 - ②\end{aligned}
It is clear that both of these lines have the same gradient m=2. That is why they do not intersect – they are parallel lines!
Lines which have the same gradient are parallel and therefore never touch each other.
Since parallel lines never intersect, they cannot be solved simultaneously.
If we try to solve these parallel lines simultaneously, we quickly run into issues. Working with equations ① and ② in their original form:
\begin{aligned}2x-y&=-1&- ① \\[12pt]2x-y&=2&- ②\end{aligned}
Action: ①-②
\begin{aligned}(2x-2x)-(-y-(-y))&=-1-2 \\[12pt]0-(-y+y)&=-3 \\[12pt]0-0&=-3 \\[12pt]0&=-3 \Large\boldsymbol{\times}\end{aligned}
On the LHS, we are left with 0 since 2x-2x=0 and -y-(-y)=-y+y=0, and on the RHS we have -3 since -1-2=-3.
0=-3 is obviously a false mathematical statement, so we have hit a maths error. What we have tried to do is impossible – the lines cannot be solved simultaneously since they never intersect!
As a final example, look at the following equations:
\begin{aligned}2x+y&=4 - ① \\[12pt]4x+2y&=8 - ②\end{aligned}
Notice that equation ② can be simplified by taking out the common factor of 2. Doing this, we have:
\begin{aligned}2x+y&=4 - ① \\[12pt]2x+y&=4 - ②\end{aligned}
After simplifying, it becomes clear that the underlying line in equation ② was actually the same as equation ① all along! So can you guess what would happen if you tried to solve them simultaneously? That’s right – you’d get another maths error! A line cannot intersect with itself after all!
Key Outcomes
Lines which have the same gradient are parallel and therefore never touch each other.
Since parallel lines never intersect, they cannot be solved simultaneously.