Number Theory is the branch of mathematics that deals with the properties of and relationships between numbers. It is a fundamental area of study which underpins our whole understanding of mathematics. It can be a complex topic, so we will not go into great depth here, but there are some elementary aspects we can use to our advantage.

The very basics of Number Theory involve defining key number sets. In mathematics, a set is a collection of distinct objects which share specific characteristics, with the set then considered as an object in its own right. Different number sets take on different characteristics, and if we know that a number lies within a specific set, then we know that it possesses the characteristics which define the set. This allows us to study numbers and how they work together more easily.

The most common sets of numbers, along with the symbols we use to represent each set, are outlined below:

The Natural Numbers, symbol ℕ, can be described in common language as “counting numbers” – the numbers that occur commonly and obviously in nature. They are the set of whole, non-negative numbers beginning with 1 and increasing by 1 at each interval going on to infinity:

ℕ: \boldsymbol{\{1, 2, 3, 4 …\}}

The Whole Numbers, symbol 𝕎, are basically just the set of Natural Numbers with the inclusion of the concept of zero:

𝕎: \boldsymbol{\{0, 1, 2, 3, 4 …\}}

Notice that the Whole Numbers include everything that was in the Natural Numbers (the set that came before it), plus zero. This will be a common theme with each subsequent number set we discuss here:

Integers, symbol ℤ, include all of the Whole Numbers plus their negative equivalents:

ℤ: \boldsymbol{\{… -3, -2, -1, 0, 1, 2, 3 …\}}

The Rational Numbers, symbol ℚ, introduces fractions (i.e. decimalisation) for the first time. So far in our number sets we have only jumped in intervals of 1, but of course you know there are numbers that lie between 1 and 2, and numbers that lie between 2 and 3, and so on. So, the Rational Numbers include all of the Integers plus all fractions of Integers:

ℚ: \boldsymbol{\{… -10, -8, -5.5, -\frac{7}{2}, -1, 0, 0.05, \frac{1}{3}, 1, \frac{9}{4}, 6 …\}}

To give a formal definition:

In the number set above I have given various random examples of Rational Numbers as it is impossible to actually write them all out in chronological order (there are infinitely many of them!) But as you can see, any one of these examples fits the formal definition of a Rational Number. Taking a few examples:

-10 is a Rational Number since it can be written as \frac{-20}{2}, and both -20 and 2 are Integers.

0.05 is a Rational Number since it can be written as \frac{1}{20}, and both 1 and 20 are Integers.

\frac{9}{4} is clearly a Rational Number since it is already written as a fraction of two Integers.

The Real Numbers, symbol ℝ, include all of the Rational Numbers, plus Irrational Numbers:

Basically, you cannot write Irrational Numbers as exact decimals. Sound familiar? Think surds! In the Surds topic we learned that surds are the exact way to represent the roots of numbers whose roots cannot be expressed exactly using decimals. Since surds cannot be expressed exactly as decimals, surds are irrational and therefore fit within the Real Number set:

ℝ: \boldsymbol{\{… -10, -5.5, -\sqrt{5}, -1, 0, \frac{1}{3}, 1, \sqrt{3}, \frac{9}{4}, \pi, 6 …\}}

In the number set above I have just given various random examples of Real Numbers as it is impossible to write them all out in chronological order (the same problem we had with writing out the Rational Numbers). To discuss a few examples:

If we try to figure out \sqrt3 as a decimal, we find \sqrt3=1.73205080757\ldots We see that we cannot find \sqrt3 as an exact decimal – it goes on forever and never starts to repeat itself. Therefore, \sqrt3 is an Irrational Number and it fits within the Real Number set.

If we try to figure out \pi as a decimal, we find \pi=3.14159265359\ldots We see that we cannot find \pi as an exact decimal – it goes on forever and never starts to repeat itself. Mathematicians and computer scientists have actually calculated \pi to trillions of decimal places and have thus far found that indeed it does seem to go on forever and never starts to repeat itself. Let’s be clear that unlike \sqrt{3}, \pi is not a surd, but it is another example of an Irrational Number (one of a special subset of the Irrational Numbers called Transcendental Numbers), and therefore it fits within the Real Number set.

The key principle here – that each new number set we defined contains all the numbers from the previous set, plus additional terms that belong in the new set – can be summarised in the diagram below which shows examples from each number set:

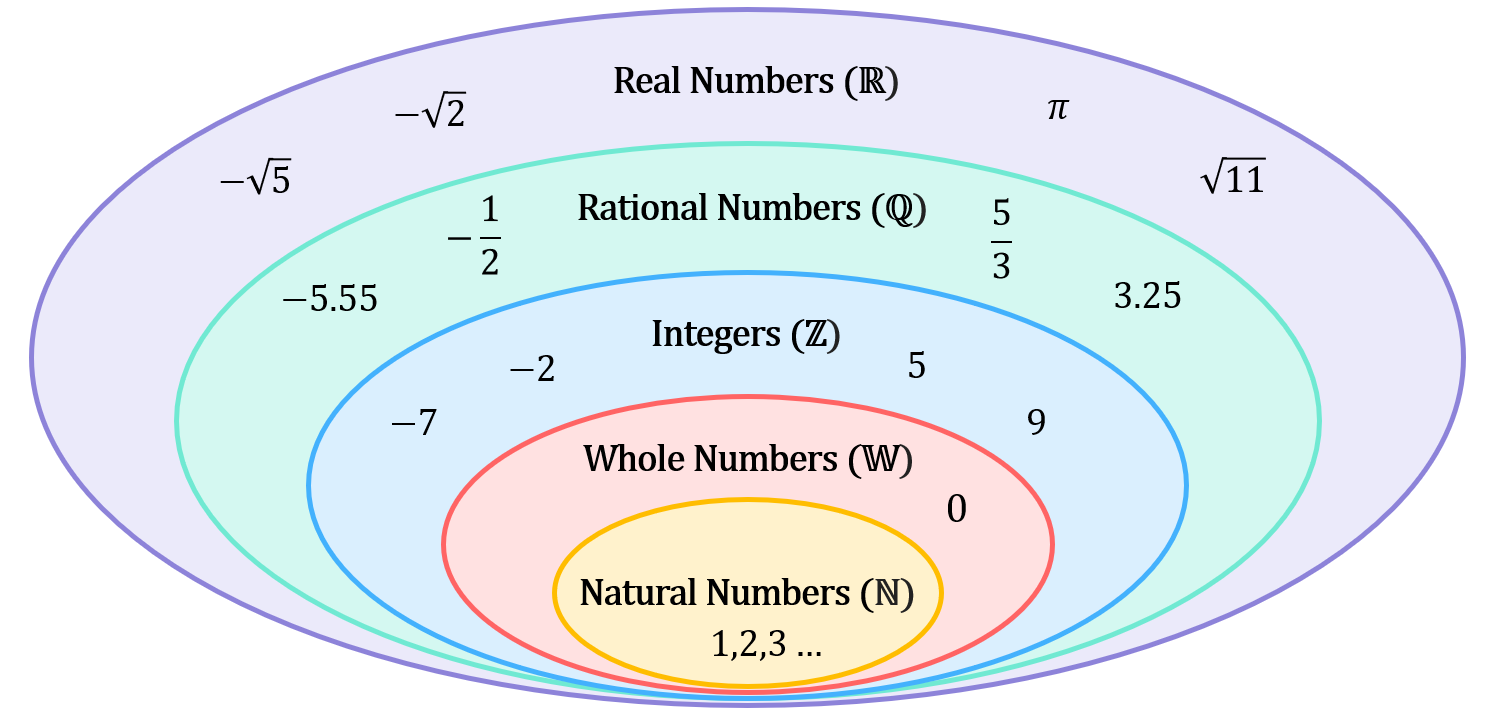
In the diagram above:

• The Natural Numbers (ℕ) stand alone.
• The Whole Numbers (𝕎) include all of the Natural Numbers, plus zero.
• The Integers (ℤ) include all of the Whole Numbers, plus their negatives.
• The Rational Numbers (ℚ) include all of the Integers, plus all fractions of Integers.
• The Real Numbers (ℝ) include all of the Rational Numbers, plus the Irrational Numbers (i.e. all surds and other special numbers like \pi).

You do not need to worry about memorising the symbols or exact definitions detailed in this section, but it is useful to know the difference between Integers, Rational Numbers and Real Numbers. Have you ever been asked to rationalise a denominator for example? You may know the process to do this, but what does that even mean? We will use the definitions we have learned here to understand this in more detail in the following topics of this module.