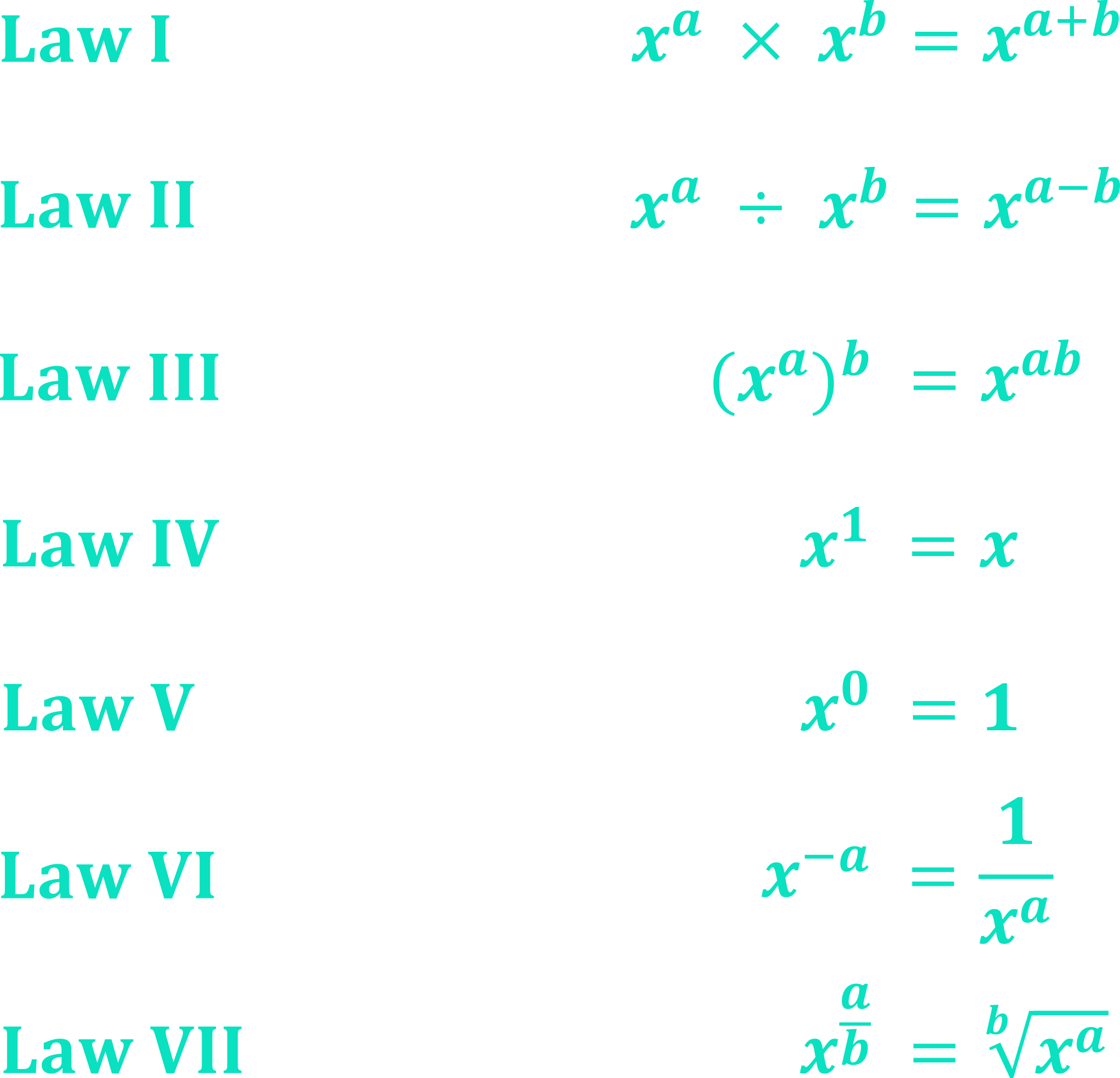What is Index Notation?
An index (or the plural “indices”) is simply a number which is raised to a power. The power tells you how many times you have to multiply the number by itself.
For example, 4^4 means you have to multiply 4 by itself 4 times:
4^4=4\times 4\times 4\times 4=256
The power is sometimes referred to as an index on its own, which can be a little confusing. It can also be called an exponent. But “index”, “power” and “exponent” are terms which all mean the same thing – they’re just talking about the little number up top!
![]()
Just as with surds, indices have their own laws which define how to manipulate and simplify them. There are seven Laws of Indices to know:
\begin{aligned}\textbf{Law I:}& \boldsymbol{x^{a}\times \ x^{b}=x^{a+b}} \\[12pt]\textbf{Law II:}& \boldsymbol{x^{a}\div \ x^{b}=x^{a-b}} \\[12pt]\textbf{Law III:}& \boldsymbol{(x^{a})^{b}=x^{ab}} \\[12pt]\textbf{Law IV:}& \boldsymbol{x^{1}=x} \\[12pt]\textbf{Law V:}& \boldsymbol{x^{0}=1} \\[8pt]\textbf{Law VI:}& \boldsymbol{x^{-a}=\frac{1}{x^{a}}} \\[12pt]\textbf{Law VII:}& \boldsymbol{x^{\large\frac{a}{b}}=\sqrt[\footnotesize b]{x^{a}}}\end{aligned}
Let’s examine each Law in turn to understand it in more detail.
\textbf{Law I:} \boldsymbol{x^{a}\times x^{b}=x^{a+b}}
Law I states that to multiply index terms you add their powers together. The reason why actually becomes fairly obvious when we break it down. Suppose we had the following problem:
\begin{aligned}x^2\times x^3\end{aligned}
According to Law I, we should write:
\begin{aligned}& x^{2}\times x^{3} \\[12pt]&=x^{2+3} \\[12pt]&=x^{5}\end{aligned}
But why do we add the powers when multiplying? Shouldn’t we also just be multiplying the powers? Since x^{2} just means x multiplied by itself twice, and x^{3} just means x multiplied by itself three times, we could instead write:
\begin{aligned}& x^{2}\times x^{3} \\[12pt]&=(xx)\times (xxx) \\[12pt]&=xxxxx \\[12pt]&=x^5\end{aligned}
As you can see, breaking the question out in this way returns the same result we obtained when using Law I directly.
Note that Law I only applies where the indices are of the same base! For example, if we had:
\begin{aligned}x^2\times y^3\end{aligned}
We would not add the powers since one of the indices is base x whilst the other is base y. In such a case, we simply “mash” the two terms together and write:
\begin{aligned}x^2\times y^3=x^2y^3\end{aligned}
\textbf{Law II:} \boldsymbol{x^{a}\div{x}^{b}=x^{a-b}}
Law II states that to divide index terms you subtract their powers. Once again, the reason why actually becomes fairly obvious when we break it down. Suppose we had the following problem:
\begin{aligned}x^6\div\ x^4\end{aligned}
According to Law II, we should write:
\begin{aligned}& x^{6}\div x^{4} \\[12pt]&=x^{6-4} \\[12pt]&=x^{2}\end{aligned}
But why do we subtract the powers when dividing? Shouldn’t we also just be dividing the powers? If we reinterpret the question as a fraction, and write the index terms in long form, the reason why we subtract the powers becomes more obvious:
\begin{aligned}& x^6\div x^4 \\[12pt]&=\frac{x^6}{x^4} \\[12pt]&=\frac{xxxxxx}{xxxx}\\[12pt]&=\frac{xx\sout{xxxx}}{\sout{xxxx}} \\[12pt]&=\frac{xx}{1} \\[12pt]&=x^2\end{aligned}
Breaking the question out in this way returns the same result we obtained when using Law II directly.
As with Law I, note that Law II only applies where the indices are of the same base!
\textbf{Law III:} \boldsymbol{(x^{a})^{b}={x}^{ab}}
Law III states that when an index is raised to a power you multiply the powers. As always, the reason why becomes fairly obvious when we break it down. Suppose we had the following problem:
(x^{2})^{3}
According to Law III, we should write:
\begin{aligned}& {(x}^2)^3 \\[12pt]&=x^{2\times 3} \\[12pt]&=x^{6}\end{aligned}
Since anything to the power 3 (“cubed”) just means multiply by itself three times, we could instead write:
\begin{aligned}& (x^2)^3 \\[12pt]&=x^2\times x^2\times x^2 \\[12pt]&=x^{2+2+2} \\[12pt]&=x^6\end{aligned}
And as you can see, breaking the question down in this way returns the same result we obtained when using Law III directly.
\textbf{Law IV:} \boldsymbol{x^{1}=x}
Law IV states that any number raised to the power 1 equals the number itself. Essentially, raising a number to the power one doesn’t do anything!
Well that was easy wasn’t it? If only all the Laws were so simple…
\textbf{Law V:} \boldsymbol{x^{0}=1}
Law V states that any number (excluding 0) raised to the power of 0 equals 1. This is the hardest Law of Indices to wrap your head around, so do not worry if it is a little confusing – you are not alone! There is an ongoing debate among mathematicians as to how 0^{0} should be defined. In fact, the most commonly accepted position at this time is that 0^{0} is not even undefined, but it is in fact indeterminate – meaning, it cannot be determined! A thorough discussion on this is well beyond the scope of this course, but for the purposes of your National 5 exam you can safely assume that anything raised to the power of 0 is simply 1.
\textbf{Law VI:} \boldsymbol{x^{-a}=\frac{1}{x^{a}}}
Law VI states that any number raised to a negative power can be written as its reciprocal with a positive power. (Note, a “reciprocal” is just a fancy way of saying “1 over”) To understand why this is the case, imagine for a moment that we do not know Law VI and we have the following problem:
\begin{aligned}{x^a\times x}^{-a}\end{aligned}
We can tackle this problem using the Laws we have already established. Recalling Law I for multiplying index terms, we have:
\begin{aligned}& x^a\times x^{-a} \\[12pt]&=x^{a+(-a)} \\[12pt]&=x^{a-a} \\[12pt]&=x^0 \\[12pt]&=1\end{aligned}
(In the last step above, we used Law V).
Now if Law VI is a valid Law, then since \begin{aligned}x^{-a}=\frac{1}{x^a}\end{aligned}, it shouldn’t matter whether we use \begin{aligned}x^{-a}\end{aligned} or \begin{aligned}\frac{1}{x^a}\end{aligned} in a question since Law VI tells us the two are equivalent. To illustrate this point, imagine if you had a question involving the number 3 – would it really matter if you used \frac{18}{6} instead of 3? Of course it wouldn’t, since \frac{18}{6} is just 3 anyway! So, if Law VI is accurate, then \begin{aligned}x^{-a}\end{aligned} and \begin{aligned}\frac{1}{x^a}\end{aligned} are actually the same thing and using either form should take us to the same end point. Attempting the problem again, this time substituting \begin{aligned}\frac{1}{x^a}\end{aligned} in place of \begin{aligned}x^{-a}\end{aligned}, we find:
\begin{aligned}& {x^a\times x}^{-a} \\[12pt]&=x^a\times \frac{1}{x^a} \\[12pt]&=\frac{x^a}{1}\times \frac{1}{x^a} \\[12pt]&=\frac{x^a}{x^a} \\[12pt]&=1\end{aligned}
Since both options lead to the same final answer, clearly it does not matter whether we use \begin{aligned}x^{-a}\end{aligned} or \begin{aligned}\frac{1}{x^a}\end{aligned}. We can therefore conclude that Law VI is true: \begin{aligned}x^{-a}=\frac{1}{x^a}\end{aligned}.
\textbf{Law VII:} \boldsymbol{x^{\large\frac{a}{b}}=\sqrt[\footnotesize b]{x^{a}}}
Law VII states that any number raised to a fractional power can be written as a surd. Law VII is something of a bridge connecting surds and indices as it equates terms in each format.
To help us understand Law VII in more detail, it is useful to first note the general definition of square roots:
\boldsymbol{\sqrt x\times \sqrt x=x}
The “square root of x” (\sqrt x) is defined to be the number than when multiplied by itself gives x. If we look at this result using non-surds, it becomes clear why this rule holds up. As an example:
\begin{aligned}\sqrt9\times\sqrt9=9\end{aligned}
Since 9 is a perfect square number we know that \sqrt9 is not a surd since \sqrt9=3. Replacing \sqrt9 with 3 gives the obvious result:
\begin{aligned}3\times 3=9\end{aligned}
In a similar vein:
\begin{aligned}\sqrt{25}\times \sqrt{25}=25\end{aligned}
Since 25 is a perfect square number we know that \sqrt{25}=5. Replacing \sqrt{25} with 5 gives the obvious result:
\begin{aligned}5\times 5=25\end{aligned}
This extends to actual surds. For example:
\begin{aligned}\sqrt7\times \sqrt7&=7 \\[12pt]\sqrt{13}\times \sqrt{13}&=13 \\[12pt]\sqrt{29}\times \sqrt{29}&=29\end{aligned}
And so on. We can therefore say in general:
\begin{aligned}\sqrt x\times \sqrt x=x\end{aligned}
With that established, lets return to understanding Law VII in more detail. To do this, again it can be useful to go back to earlier Laws we have already established. Take the example:
\begin{aligned}& x^{\large\frac{1}{2}}\times x^{\large\frac{1}{2}} \\[12pt]&=x^{\large\frac{1}{2}+\large\frac{1}{2}} \\[12pt]&=x^1 \\[12pt]&=x\end{aligned}
And we also have the standard result:
\begin{aligned}\sqrt x\times \sqrt x=x\end{aligned}
In doing x^{\large\frac{1}{2}}\times x^{\large\frac{1}{2}}, we are actually doing (x^{\large\frac{1}{2}})^2 (i.e. x^{\large\frac{1}{2}} multiplied by itself). And obviously, we know that \sqrt x\times \sqrt x=(\sqrt x)^2=x.
So, it seems that squaring x^{\large\frac{1}{2}} and squaring \sqrt x both lead to x:
\begin{aligned}(x^{\large\frac{1}{2}})^2=(\sqrt x)^2&=x\end{aligned}
So we can say:
\begin{aligned}(x^{\large\frac{1}{2}})^2&=(\sqrt x)^2 \\[12pt]x^{\large\frac{1}{2}}&=\sqrt x\end{aligned}
The last line of this working now starts to resemble something similar to the form of Law VII showing an index being converted into a surd:
\begin{aligned}\text{Law VII:}& x^{\large\frac{a}{b}}=\sqrt[\footnotesize b]{x^a} \\[12pt]\text{Last line of working:}& x^{\large\frac{1}{2}}=\sqrt x\end{aligned}
But where have the 1 and 2 from the LHS gone? They are actually still there, we just don’t show them!
\begin{aligned}x^{\large\frac{1}{2}}=\sqrt x=\sqrt[\footnotesize 2]{x^1}\end{aligned}
In this specific case, we don’t show the 2 since the \sqrt{} symbol already means “square root” without the need to show the 2. We only show the little number on the outside of a root when we mean something higher than the square root, such as the cubed root (\sqrt[\footnotesize3]{}) or the fourth root (\sqrt[\footnotesize4]{}) etc. And the 1 as the power of x makes no difference, as we already know from Law IV, so it was not shown. But in the end, we have a converted a fractional index term into a surd which follows the exact layout prescribed by Law VII:
\begin{aligned}\text{Law VII:}& x^{\large\frac{a}{b}}=\sqrt[\footnotesize b]{x^a} \\[12pt]\text{Last line of working:}& x^{\large\frac{1}{2}}=\sqrt x=\sqrt[\footnotesize2]{x^1}\end{aligned}
Now this is not a formal proof (which would be beyond the scope of this course) but this example should give you some comfort as to why Law VII is the correct method to change a fractional index term into a surd.
With Law VII, people often forget which way round the a and b terms go when changing from an index to a surd. In order to remember this, just remember the example that we have discussed here:
\begin{aligned}\text{Law VII:}& x^{\large\frac{a}{b}}=\sqrt[\footnotesize b]{x^a} \\[12pt]\text{Example to remember:}& x^{\large\frac{1}{2}}=\sqrt[\footnotesize2]{x^1}\end{aligned}
Anything raised to a power \boldsymbol{\frac{1}{2}} is the same thing as square root. If you remember that, then you’ll know which way around the 2 and 1 go, and therefore you’ll know the correct order for any other example. Some additional examples are shown below:
\begin{aligned}\text{Law VII:}& x^{\large\frac{a}{b}}=\sqrt[\footnotesize b]{x^a} \\[12pt]\text{Example to remember:}& x^{\large\frac{1}{2}}=\sqrt[\footnotesize 2]{x^1} \\[12pt]\text{Additional example 1:}& x^{\large\frac{2}{3}}=\sqrt[\footnotesize3]{x^2} \\[12pt]\text{Additional example 2:}& x^{\large\frac{4}{5}}=\sqrt[\footnotesize5]{x^4} \\[12pt]\text{Additional example 3:}& x^{\large\frac{9}{4}}=\sqrt[\footnotesize4]{x^9}\end{aligned}
Key Outcomes
Indices are numbers which have been raised to a power.
Power, index and exponent all mean the same thing.
There are seven Laws of Indices to know:
\textbf{Law I:} \boldsymbol{x^a\times x^b=x^{a+b}}
“To multiply index terms, you add their powers together”
Law I only applies where the indices are of the same base.
\textbf{Law II:} \boldsymbol{x^a\div x^b=x^{a-b}}
“To divide index terms, you subtract their powers”
Law II only applies where the indices are of the same base.
\textbf{Law III:} \boldsymbol{{(x}^a)^b=x^{ab}}
“When an index is raised to a power you multiply the powers”
\textbf{Law IV:} \boldsymbol{x^1=x}
“Any number raised to the power 1 equals the number itself”
\textbf{Law V:} \boldsymbol{x^0=1}
“Any number raised to the power of 0 equals 1”
\textbf{Law VI:} \boldsymbol{x^{-a}=\frac{1}{x^a}}
“Any number raised to a negative power can be written as its reciprocal with a positive power”
\textbf{Law VII:} \boldsymbol{x^{\large\frac{a}{b}}=\sqrt[\footnotesize b]{x^a}}
“Any number raised to a fractional power can be written as a surd”
The definition of a square root states that: \sqrt x\times \sqrt x=x
Anything raised to a power \frac{1}{2} is the same thing as square root: x^{\large\frac{1}{2}}=\sqrt[\footnotesize 2]{x^1}=\sqrt x