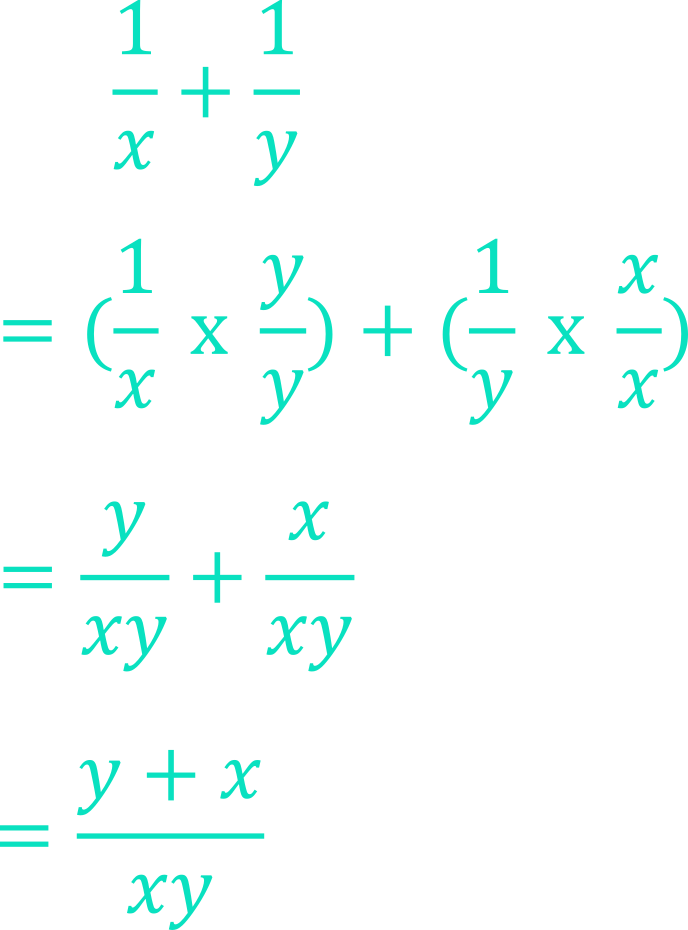Fractions
At the National 5 level it is important to know how to multiply, divide, add and subtract fractions. We look at each of these operations in turn below:
Multiplying Fractions
Multiplying fractions is straightforward: you simply multiply the numerators together to get the new numerator, and multiply the denominators together to get the new denominator. Or, “multiply the tops and multiply the bottoms” for short.
Example 1
\begin{aligned}\frac{1}{2}\times \frac{1}{2}=\frac{1\times1}{2\times2}=\frac{1}{4}\end{aligned}
Example 2
\begin{aligned}\frac{2}{3}\times \frac{2}{3}=\frac{2\times 2}{3\times 3}=\frac{4}{9}\end{aligned}
And as always, where it is possible to do so you must simplify fractions as in the following example:
Example 3
\begin{aligned}\frac{3}{4}\times \frac{6}{8}=\frac{3\times 6}{4\times 8}=\frac{18}{32}\end{aligned}
Now we simplify \large\frac{18}{32} to get the final answer:
\begin{aligned}\frac{18}{32}=\frac{\sout2\times 9}{\sout2\times 16}=\frac{9}{16}\end{aligned}
Dividing Fractions
Dividing fractions is also fairly straightforward: you simply flip the top and bottom numbers of the divisor around (note, the divisor is the second fraction), change the division sign to a multiplication sign, and multiply the two fractions normally. Or, “flip the second fraction and multiply” for short.
Example 1
\begin{aligned}\frac{1}{2}\div\frac{1}{2}&=\frac{1}{2}\times\frac{2}{1} \\[12pt]&=\frac{1\times 2}{2\times 1} \\[12pt]&=\frac{2}{2}=1\end{aligned}
Example 2
\begin{aligned}\frac{3}{4}\div \frac{3}{5}&= \frac{3}{4}\times\frac{5}{3}=\frac{3\times5}{4\times3}=\frac{15}{12}\end{aligned}
Now we simplify \large\frac{15}{12} to get the final answer:
\begin{aligned}\frac{15}{12}=\frac{\sout3\times5}{\sout3\times4}=\frac{5}{4}\end{aligned}
Adding and Subtracting Fractions
A key principle in mathematics is that like-terms add together, or stack up.
x+x=2x. y+y=2y. But x+y=… that just equals x+y, that’s the only way to express it because the terms are different – they do not stack up.
To offer a rather silly real-life analogy:
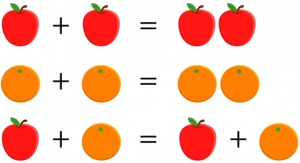
An apple plus an apple equals two apples. An orange plus an orange equals two oranges. But an apple plus an orange… that’s just an apple plus an orange. We can’t combine them – they don’t add up! This is because apples and oranges are not like-terms; they are different objects.
Like-terms stack together, unlike-terms do not.
We face this same obstacle when it comes to adding or subtracting fractions. Think of fractions as follows:
\begin{aligned}\frac{\text{numerator}}{\text{denominator}}=\frac{\text{determines}\ \textbf{how many}\ \text{of the fraction}}{\text{determines}\ \textbf{the type}\ \text{of fraction}}\end{aligned}
For example:
\begin{aligned}\frac{2}{3}=\frac{\textbf{how many}\ \text{of the fraction -}\ \textbf{two}}{\textbf{the type}\ \text{of fraction -}\ \textbf{thirds}}\end{aligned}
Thinking of fractions in this way makes it clear why trying to add or subtract fractions with different denominators presents a problem. Since the denominator determines the type of fraction, fractions with the same denominator are like-terms, and as we have established, like-terms stack together. Fractions with different denominators are therefore not like-terms, so they do not stack together. When the denominators are different, then we need to adjust the fractions to make sure they have the same denominators before we attempt to add them together.
There are three possible scenarios you may face when trying to add fractions:
1) The fractions have the same denominators
2) The fractions have different denominators, but one is a factor of the other
3) The fractions have different denominators, and neither is a factor of the other
Let’s explore each possibility in turn:
1) The fractions have the same denominators
This is the most straightforward scenario. As the fractions have the same denominators, they are both the same type of fraction (i.e. they are like-terms), so they add without any trouble:
Example 1
\begin{aligned}\frac{1}{4}+\frac{7}{4}=\frac{8}{4}\end{aligned}
(1 of a thing, plus 7 of the same thing, is 8 of that thing – simple)
Then as always, we must simplify:
\begin{aligned}\frac{8}{4}=2\end{aligned}
Example 2
\begin{aligned}\frac{2}{3}+\frac{2}{3}=\frac{4}{3}\end{aligned}
(2 of a thing, plus 2 more of the same thing, equals 4 of that thing)
Before looking at the next two scenarios, let’s introduce an extremely helpful rule we will use extensively when manipulating fractions:
\begin{aligned}\boldsymbol{\frac{x}{1}={x}} \textbf{Anything divided by 1 is itself.}\end{aligned}
Or, rearranging the equation:
\begin{aligned}\boldsymbol{\frac{x}{x}={1}} \textbf{Anything divided by itself is 1.}\end{aligned}
Keep these rules in mind as we attempt the rest of the examples.
2) The fractions have different denominators, but one is a factor of the other
When the fractions have different denominators, we have a problem. Having different denominators means the fractions are not like-terms, so we cannot add them in their current form (just like we could not do apple + orange). We have to make adjustments to one of the fractions to make the denominators the same before we can add them.
Let’s take a simple example:
\begin{aligned}\frac{1}{2}+\frac{1}{4}\end{aligned}
Halves and quarters are different types of fractions, so we cannot add them directly. However, we can picture these basic fractions on pie charts to easily understand what their sum would be:
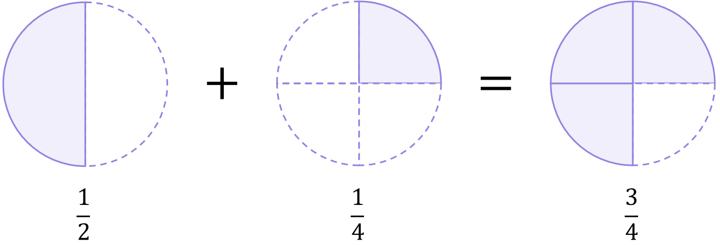
Therefore, we know that:
\begin{aligned}\frac{1}{2}+\frac{1}{4}=\frac{3}{4}\end{aligned}
But of course you won’t have handy pie charts to help you in an exam, so to do this question you would have to adjust the fractions and make them like-terms.
One of the fractions has a denominator of 2 and the other has a denominator of 4. Notice that 2 is a factor of 4 (2 fits into 4 perfectly), thus we can make an adjustment as follows:
\begin{aligned}& \frac{1}{2}+\frac{1}{4} \\[12pt]&=\left(\frac{1}{2}\times\frac{2}{2}\right)+\frac{1}{4}\end{aligned}
Here I have chosen to multiply the \large\frac{1}{2} fraction by \large\frac{2}{2}, and I haven’t done anything to the \large\frac{1}{4}fraction. So why have I done this and why is it ok to adjust only one of the fractions without also adjusting the other? Remember the rule:
\begin{aligned}\boldsymbol{\frac{x}{x}=1} \textbf{Anything divided by itself is 1.}\end{aligned}
Therefore {\large\frac{2}{2}}=1, so in multiplying the \large\frac{1}{2} by \large\frac{2}{2}, I’m really just multiplying it by 1. Multiplying something by 1 doesn’t change its value, so this is always ok to do. But why did I specifically choose to multiply the \large\frac{1}{2} by \large\frac{2}{2}, since I could have multiplied it by anything that was equivalent to 1? Continuing the working below, we see that multiplying the \large\frac{1}{2} by \large\frac{2}{2} results in the denominators of the two fractions becoming equal:
\begin{aligned}&=\left(\frac{1}{2}\times\frac{2}{2}\right)+\frac{1}{4} \\[12pt]&=\frac{2}{4}+\frac{1}{4} \\[12pt]&=\frac{3}{4}\end{aligned}
If we return to the pie charts, we can see that the \large\frac{1}{2} pie we used originally is actually the same as a \large\frac{2}{4} pie, which should give you confidence that changing \large\frac{1}{2} into \large\frac{2}{4} was mathematically correct and did not change the value the fraction represents. If you put \large\frac{1}{2} or \large\frac{2}{4} into your calculator, you will see that as a decimal they are both equal to 0.5. The fractions look different, but they represent the same underlying value:
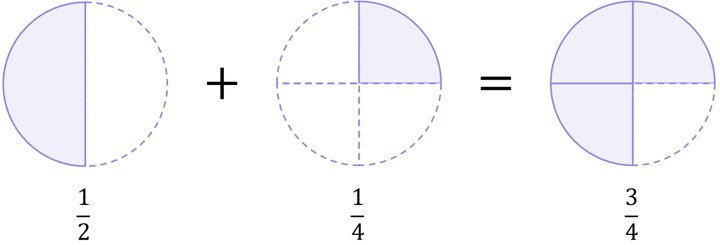
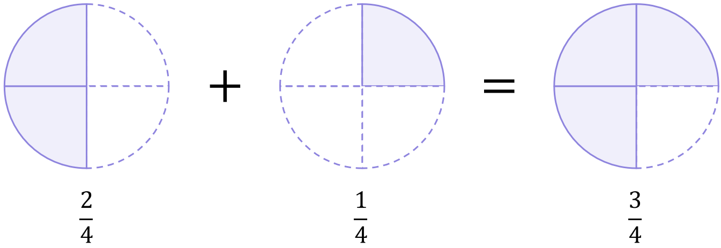
And so, both cases lead to \large\frac{3}{4}:
\begin{aligned}\frac{1}{2}+\frac{1}{4}&=\frac{3}{4} \\[12pt]\frac{2}{4}+\frac{1}{4}&=\frac{3}{4}\end{aligned}
Let’s try another example:
\begin{aligned}\frac{1}{5}+\frac{7}{15}\end{aligned}
Fifths and fifteenths are different types of fractions, so again we cannot add them directly algebraically and we need to make an adjustment. Notice that 5 is a factor of 15 (5 fits into 15 exactly), so we can make an adjustment as follows:
\begin{aligned}& \frac{1}{5}+\frac{7}{15} \\[12pt]&=\left(\frac{1}{5}\times\frac{3}{3}\right)+\frac{7}{15} \\[12pt]&=\frac{3}{15}+\frac{7}{15} \\[12pt]&=\frac{10}{15}=\frac{2}{3}\end{aligned}
Again, we can use pie charts as a visual aid to help us understand why converting \large\frac{1}{5} into \large\frac{3}{15} was mathematically correct and did not change the value the fraction represents:
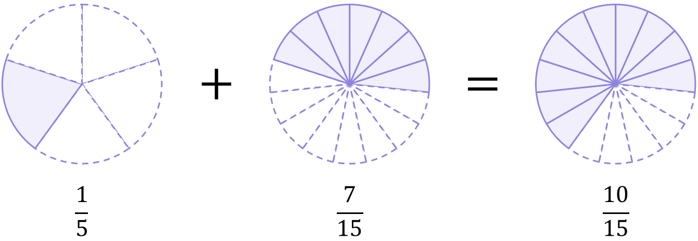
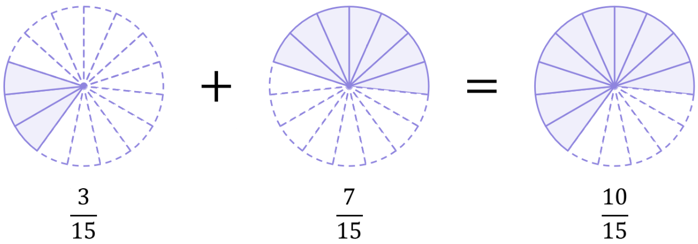
And so, both cases lead to \large\frac{10}{15}:
\begin{aligned}\frac{1}{5}+\frac{7}{15}&=\frac{10}{15} \\[12pt]\frac{3}{15}+\frac{7}{15}&=\frac{10}{15}\end{aligned}
And of course, \large\frac{10}{15} must always be simplified down to \large\frac{2}{3}:
\begin{aligned}\frac{10}{15}=\frac{\sout5\times2}{\sout5\times3}=\frac{2}{3}\end{aligned}
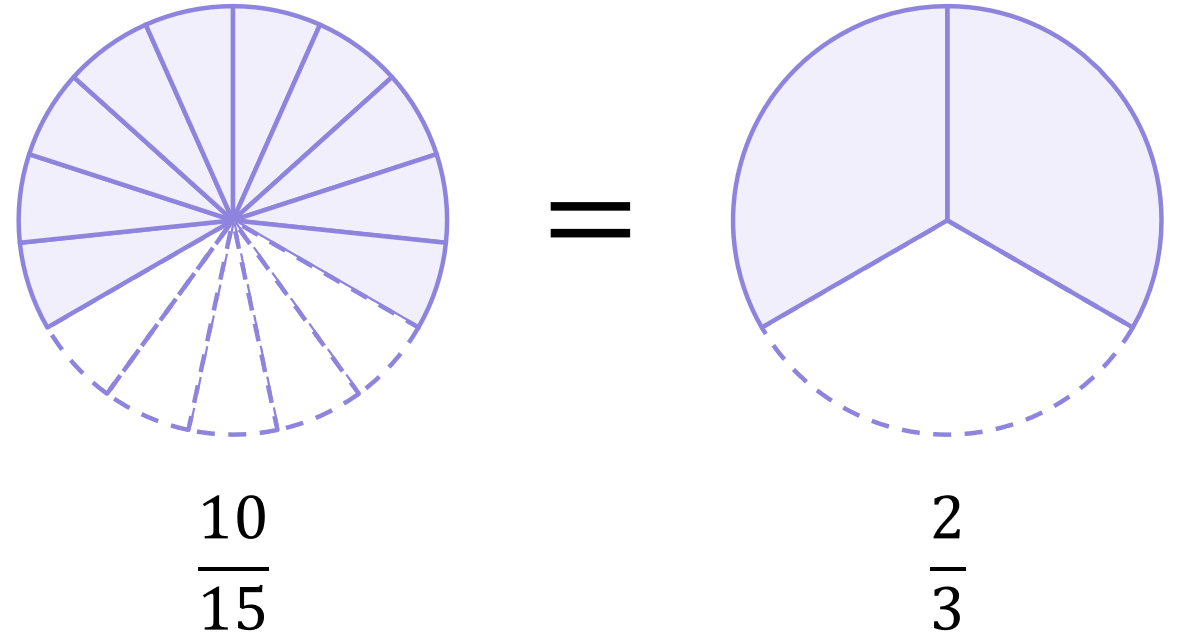
3) The fractions have different denominators, and neither is a factor of the other
Here we face a similar problem. As the denominators are different, we can’t add the fractions without first making adjustments. However, since neither denominator is a factor of the other, adjusting one fraction will not be enough. In such a case, we have to adjust both fractions.
In an earlier example we had halves and quarters, but we were able to convert the halves into quarters (since 2 is a factor of 4) and then add the fractions easily:
\begin{aligned}\frac{1}{2}&+\frac{1}{4} \\[12pt]=\frac{2}{4}&+\frac{1}{4} \\[12pt]=\frac{3}{4}\end{aligned}
In another example we had fifths and fifteenths, but we were able to convert the fifths into fifteenths (since 5 is a factor of 15) and then add the fractions easily:
\begin{aligned}\frac{1}{5}&+\frac{7}{15} \\[12pt]=\frac{3}{15}&+\frac{7}{15} \\[12pt]=\frac{10}{15}&=\frac{2}{3}\end{aligned}
But what if we had the following scenario:
\begin{aligned}\frac{1}{2}+\frac{1}{3}\end{aligned}
We have halves and thirds which are different types of fractions, so as before we cannot add them directly and we need to make adjustments. But, since 2 is not a factor of 3, and 3 is not a factor of 2, we cannot convert both fractions into either halves or thirds. Instead, we must convert the denominators of both fractions into the lowest common denominator.
The lowest common multiple of 2 and 3 (i.e. the lowest number that 2 and 3 both fit into perfectly) is 6. This is therefore the lowest common denominator of halves and thirds, so we want to turn both fractions into sixths (i.e. \large\frac{1}{6} format). To do this, we will multiply each fraction as follows:
\begin{aligned}& \frac{1}{2}+\frac{1}{3} \\[12pt]&=\left(\frac{1}{2}\times\frac{3}{3}\right)+\left(\frac{1}{3}\times \frac{2}{2}\right) \\[12pt]&=\frac{3}{6}+\frac{2}{6} \\[12pt]&=\frac{5}{6}\end{aligned}
Initially, it would appear that in multiplying the \large\frac{1}{2} by \large\frac{3}{3}, and the \large\frac{1}{3} by \large\frac{2}{2}, that I am doing different things to each fraction, which would not be ok as you know, since in algebra what you do to one term you must do to all terms. However, since {\large\frac{3}{3}}=1, and {\large\frac{2}{2}}=1, I am actually just multiplying both fractions by 1 written in different ways (remember, {\large\frac{x}{x}}=1, anything divided by itself is 1).
Once again, we can use pie charts as a visual aid to help us understand why this correct:
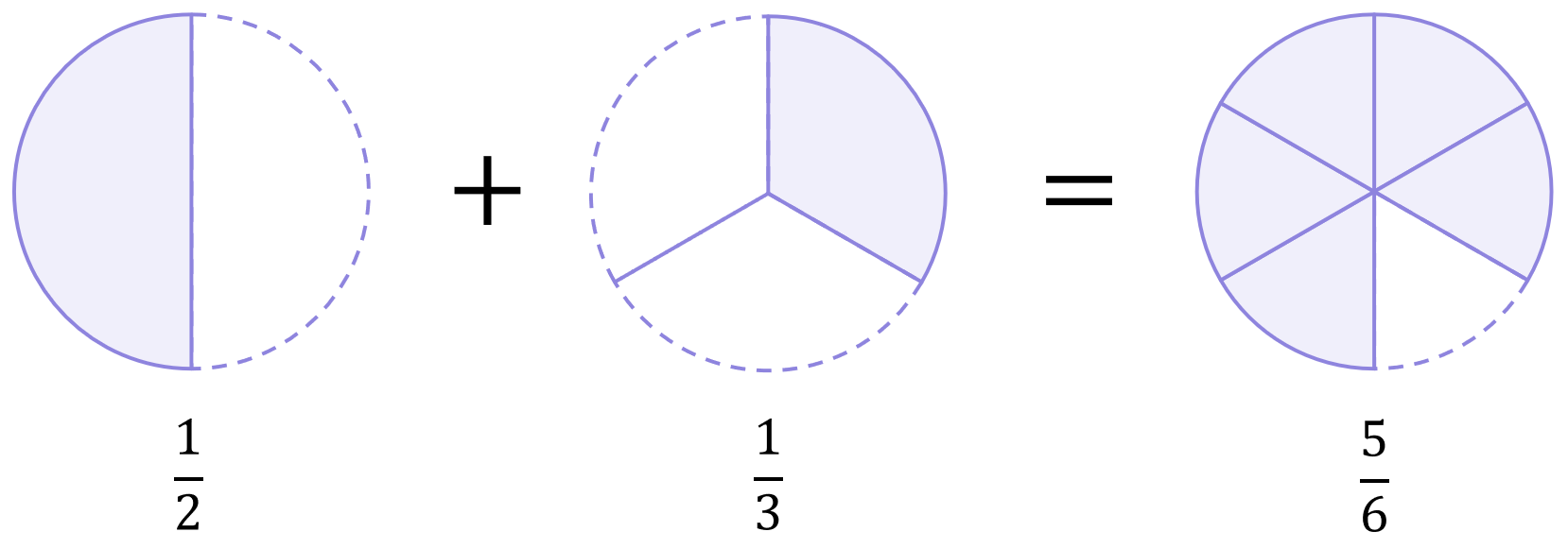
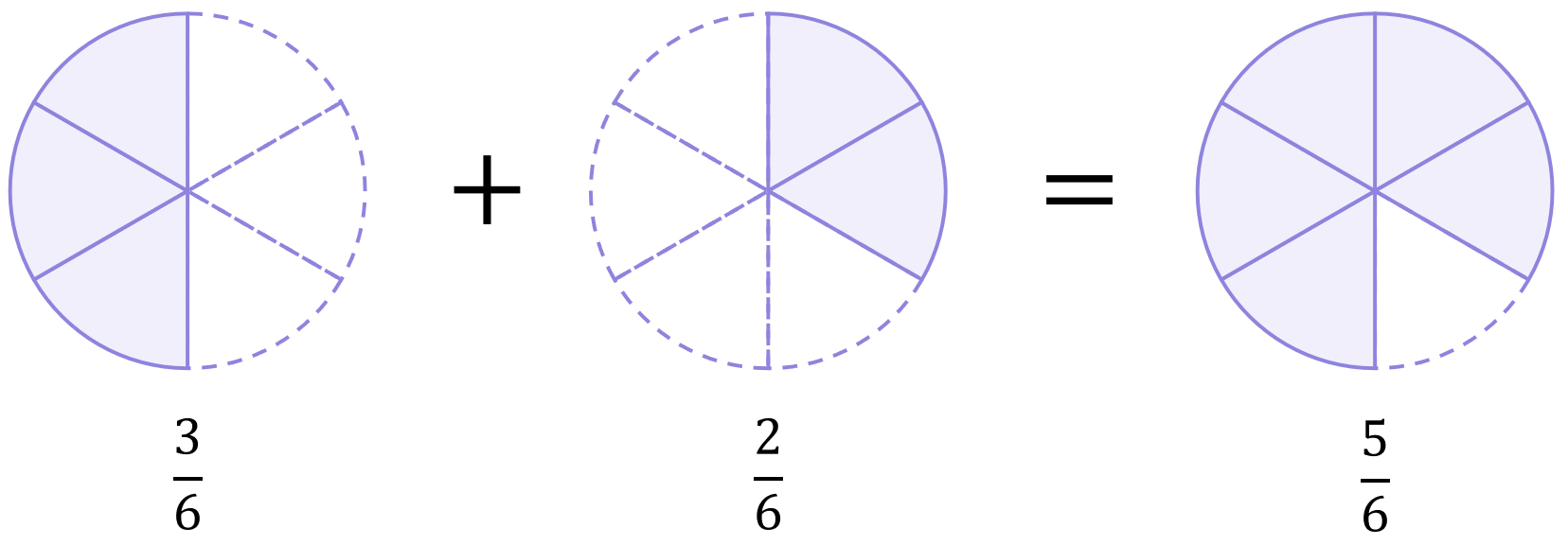
And so, both cases lead to :
\begin{aligned}\frac{1}{2}+\frac{1}{3}&=\frac{5}{6} \\[12pt]\frac{3}{6}+\frac{2}{6}&=\frac{5}{6}\end{aligned}
The steps are always the same when trying to add fractions in this situation:
1) Establish the lowest common multiple of the two denominators
2) Adjust each fraction so that they each have the lowest common multiple as their denominator
3) Add the fractions and simplify fully
Try the following examples to get used to these steps:
Example 3
\begin{aligned}\frac{2}{3}+\frac{1}{4}\end{aligned}
The lowest common multiple of 3 and 4 is 12, so both fractions should have 12 as their denominator:
\begin{aligned}&=\left(\frac{2}{3}\times\frac{4}{4}\right)+\left(\frac{1}{4}\times\frac{3}{3}\right) \\[12pt]&=\frac{8}{12}+\frac{3}{12} \\[12pt]&=\frac{11}{12}\end{aligned}
Example 4
\begin{aligned}\frac{1}{2}+\frac{4}{9}\end{aligned}
The lowest common multiple of 2 and 9 is 18, so both fractions should have 18 as their denominator:
\begin{aligned}&=\left(\frac{1}{2}\times\frac{9}{9}\right)+\left(\frac{4}{9}\times\frac{2}{2}\right) \\[12pt]&=\frac{9}{18}+\frac{8}{18} \\[12pt]&=\frac{17}{18}\end{aligned}
One final scenario to highlight would be a case where we have both a normal number and a fraction:
\begin{aligned}3+\frac{2}{5}\end{aligned}
This a mix we have not encountered yet. This problem would be easier if both elements were fractions (since we are now very comfortable with adding two fractions), so we must turn the 3 into a fraction. Remembering the rule, {\large\frac{x}{1}}=x, anything divided by 1 is itself, we can easily turn 3 into a fraction by putting it “over” 1:
\begin{aligned}3&+\frac{2}{5} \\[12pt]=\frac{3}{1}&+\frac{2}{5}\end{aligned}
We’re now back to the standard problem where we have to add two fractions with different denominators, so we just follow the usual process:
The lowest common multiple of 1 and 5 is 5, so both fractions should have 5 as their denominator. This only requires adjusting one of the fractions since the other already has a denominator of 5:
\begin{aligned}&=\left(\frac{3}{1}\times\frac{5}{5}\right)+\frac{2}{5} \\[12pt]&=\frac{15}{5}+\frac{2}{5} \\[12pt]&=\frac{17}{5}\end{aligned}
Subtracting fractions
All of the examples in this topic thus far have considered adding fractions only, so what about subtracting them? Subtracting fractions is difficult for the same reason that adding them is difficult – the fractions have to be like-terms (i.e. their denominators have to be the same).
Well, the good news is that having just learned how to add fractions, you already know everything you need to know to be able to subtract them as well! Literally the only difference with subtracting fractions is that once you’ve made the denominators of the fractions the same, you subtract them instead of adding them (obviously!)
Here are a few examples of subtracting fractions which use exactly the same techniques we learned when adding them:
Example 5
\begin{aligned}\frac{4}{3}&-\frac{1}{3} \\[12pt]=\frac{3}{3}&=1\end{aligned}
Example 6
\begin{aligned}\frac{7}{8}&-\frac{1}{2} \\[12pt]=\frac{7}{8}&-\left(\frac{1}{2}\times\frac{4}{4}\right) \\[12pt]=\frac{7}{8}&-\frac{4}{8} \\[12pt]=\frac{3}{8}\end{aligned}
Example 7
\begin{aligned}\frac{3}{5}-\frac{3}{4}\end{aligned}
The lowest common multiple of 5 and 4 is 20, so both fractions should have 20 as their denominator:
\begin{aligned}&=\left(\frac{3}{5}\times\frac{4}{4}\right)-\left(\frac{3}{4}\times\frac{5}{5}\right) \\[12pt]&=\frac{12}{20}-\frac{15}{20} \\[12pt]&=-\frac{3}{20}\end{aligned}
Key Outcomes
To multiply fractions together, multiply the tops (numerators) and multiply the bottoms (denominators). Always simplify where possible.
To divide fractions, flip the second fraction and multiply as normal. Always simplify where possible.
Like-terms stack together, unlike-terms do not.
To add or subtract fractions they must be like-terms (i.e. their denominators must be equal).
\begin{aligned}\frac{x}{1}=x \text{Anything divided by 1 is itself.} \\[12pt]\frac{x}{x}=1 \text{Anything divided by itself is 1.}\end{aligned}
Multiplying by 1 can change the way a fraction looks, which can be helpful, but it doesn’t change the value it represents. Since multiplying by 1 does not change the value of a fraction, it is always ok to do.