What is Factorising?
Factorising is a technique that can be used to calculate the roots (\boldsymbol{x}-intercepts) of quadratic functions. There are various ways to factorise (and we will discuss each of them in turn), but the principle of factorising itself is not new to you. You will already be familiar with the idea of a common factor: for example, 3 is a common factor of 6 and 21 since 3 “fits into” 6 twice (3\times 2=6) and 3 “fits into” 21 seven times (3\times 7=21).
In fact, you use the idea of common factors all the time when simplifying fractions. You know by now that:
\begin{aligned}\frac{21}{6}=\frac{7}{2}\end{aligned}
But the step you normally don’t write down shows the numerator and denominator being broken out into factors (i.e. numbers which multiply to give the original number), with the common factor of 3 then cancelling out:
\begin{aligned}\frac{21}{6}=\frac{\sout 3\times 7}{\sout 3\times 2}=\frac{7}{2}\end{aligned}
The above is an example of factorisation by common factor, which is the most basic form of factorising. Pulling out the common factor has turned both the numerator and denominator into products instead of standalone numbers, which allows for cancellation (see the “Cancelling terms and simplifying” topic for more detail).
Before we discuss factorising more complex terms like quadratics, we first need to understand a very important point about products that are equal to zero.
Suppose we have two unknown terms, a and b, and we are told that their product is 24:
\begin{aligned}a\times b=24\end{aligned}
What does this tell us about a and b? Not much really, since lots of different possible values of a and b could multiply to give 24:
\begin{aligned}a\times b&=1\times 24=24 \\[12pt]a\times b&=2\times 12=24 \\[12pt]a\times b&=3\times 8=24 \\[12pt]a\times b&=4\times 6=24\end{aligned}
And some more obscure possibilities:
\begin{aligned}a\times b&=2.5\times 9.6=24 \\[12pt]a\times b&=4.8\times 5=24 \\[12pt]a\times b&=7.5\times 3.2=24\end{aligned}
So, in fact, knowing that the product of \boldsymbol{a} and \boldsymbol{b} is 24 tells us literally nothing about \boldsymbol{a} and \boldsymbol{b} – without further information, there are infinite possibilities for the values of a and b!
However, suppose again we have two unknown terms a and b, but this time we are told that their product is 0:
\begin{aligned}a\times b=0\end{aligned}
This is a different ball game. The only possible way that the product of \boldsymbol{a} and \boldsymbol{b} can be 0 is if either: \boldsymbol{a=0}, \boldsymbol{b=0} or both \boldsymbol{a} & \boldsymbol{b=0}.
Suppose the value of b was known, say b=10. If we make a=0, then:
\begin{aligned}a\times b=0\times 10=0\end{aligned}
Since any number multiplied by 0 is 0.
On the other hand, suppose the value of a was known, say a=4. If we make b=0, then again:
\begin{aligned}a\times b=4\times 0=0\end{aligned}
Since any number multiplied by 0 is 0.
And it is obviously true that if both a & b=0, then:
\begin{aligned}a\times b=0\times 0=0\end{aligned}
In summary:
Knowing that the product of \boldsymbol{a} and \boldsymbol{b} is zero actually provides useful information about \boldsymbol{a} and \boldsymbol{b}.
The only possible way that \boldsymbol{a\times b=0} can be true is if either: \boldsymbol{a=0}, \boldsymbol{b=0} or both \boldsymbol{a} & \boldsymbol{b=0}.
The above opens up separate avenues of investigation where each avenue has only one unknown term and can therefore be solved. This is a critical point to grasp which we will use extensively when solving quadratic equations.
Returning to quadratics, recall that we use the technique of factorising to help us calculate the roots. When factorising quadratics, there are three possible methods of factorisation you may need:
1) Common factor
2) Difference of two squares
3) Trinomial (double brackets)
On occasion, more than one of these methods can be required to get to a final simplified answer. Let’s understand each of these in more detail:
Common Factor
Factorisation by common factor is the most basic form of factorising.
Suppose we have the quadratic y=x^{2}+3x and we are interested in finding the roots (x-intercepts). At the x-intercept of any function, y=0, so we should substitute y=0 into the equation and solve. Doing this gives:
\begin{aligned}x^{2}+3x=0\end{aligned}
Solving this requires factorising as the multiple x terms with different powers make it impossible to rearrange the equation in the usual fashion to make x the subject (try it yourself, you’ll quickly run into problems…)
Notice that there is a common factor of x. If it is possible to pull out a common factor, you should always do so. Factorising this out gives:
\begin{aligned}x(x+3)=0\end{aligned}
Pulling out the common factor has taken us from x^{2}+3x=0, where the LHS is a sum (i.e. adding or subtracting), to x(x+3)=0, where the LHS is a product (i.e. multiplying). This is a crucial difference.
We now have a product of two terms that is equal to zero – this is desirable as it opens up two separate and simpler avenues of investigation.
The only possible way that the product of x and (x+3) can be 0 is if either:
\begin{aligned}x=0 \text{or} (x+3)=0\end{aligned}
Clearly the x=0 option requires no further work – this is a valid solution and therefore this is the first root of the quadratic. The (x+3)=0 option can be easily rearranged and solved:
\begin{aligned}x+3&=0 \\[6pt]x&=-3\end{aligned}
Therefore, the second root is found where x=-3.
Altogether then, we have calculated that the first root of this quadratic can be found where x=0, and the second where x=-3. Since roots are actual locations (or points) on a graph, it is very important to state your roots in \boldsymbol{(x, y)} coordinate form.
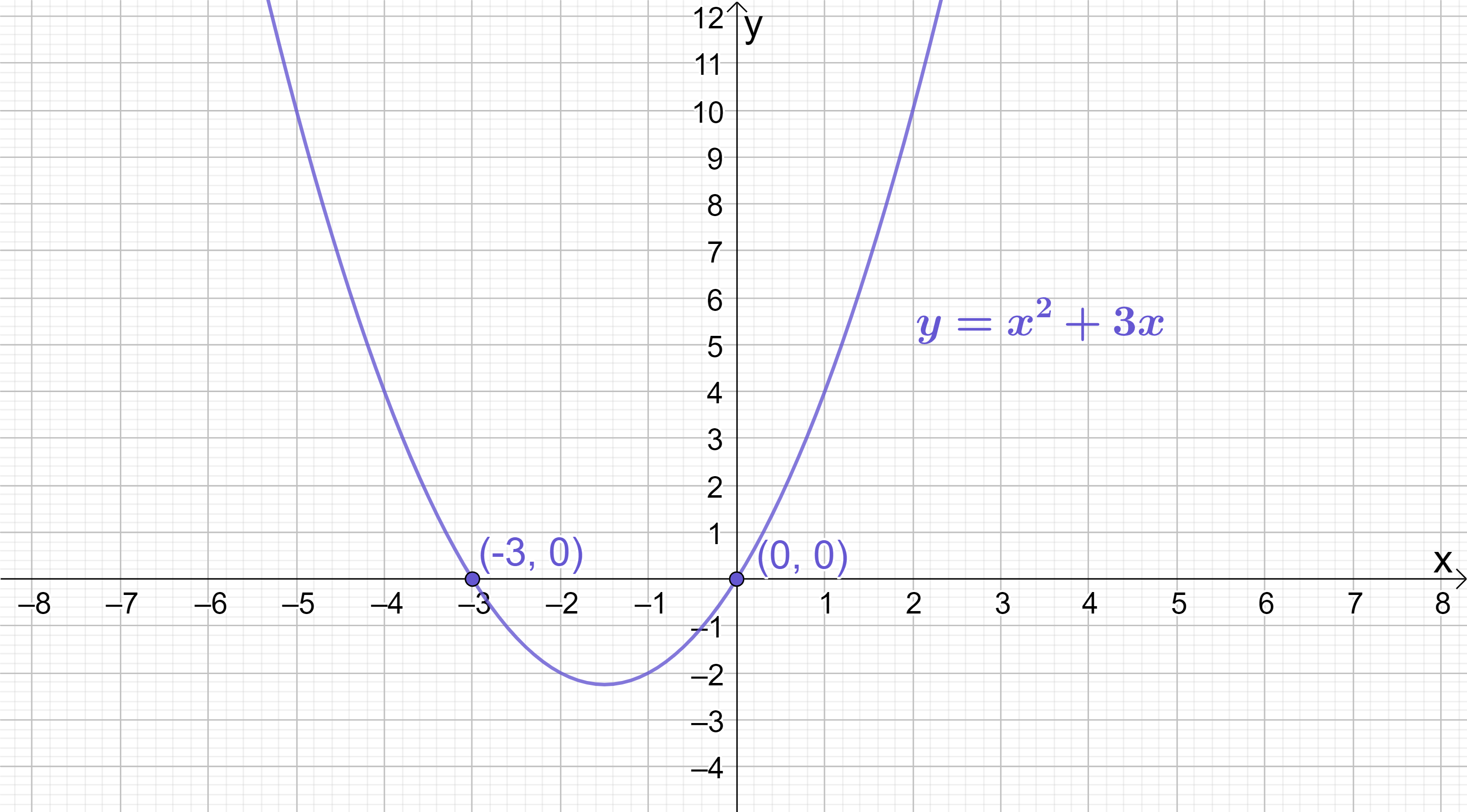
In summary, using factorisation by common factor we have calculated that the quadratic y=x^{2}+3x has roots at (0, 0) and (-3, 0) (remember: at the x-intercepts of any function, y always equals 0).
Sketching y=x^{2}+3x confirms that the roots do indeed lie at (0, 0) and (-3, 0):
Difference of Two Squares
Suppose this time the quadratic in question was y=x^{2}-4. As always, if we are trying to find the roots we should substitute y=0 into the equation and solve. Doing this gives:
\begin{aligned}x^{2}-4=0\end{aligned}
This time, there are no common factors to pull out, so we need a different method of factorisation. In this case, we should use the difference of two squares technique.
It should always be extremely easy to spot when the difference of two squares technique is required as the quadratic will:
- only have two terms;
- both of the terms will be square numbers; and
- the terms will be subtracting from one another.
It is clear that y=x^{2}-4 fits this criteria: there are only two terms, both x^{2} and 4 are square numbers (i.e. they both have perfect square roots: \sqrt{x^{2}}=x, \sqrt{4}=2), and indeed the terms are subtracting from one another.
To factorise using the difference of two squares, split the quadratic into two brackets: the first bracket will be the the square root of the first term minus the square root of the second term; the second bracket will be the square root of the first term plus the square root of the second term.
So, for x^{2}-4, since \sqrt{x^{2}}=x and \sqrt{4}=2 we have:
\begin{aligned}x^{2}-4&=0 \\[12pt](x-2)(x+2)&=0\end{aligned}
As a quick check, if we multiply the brackets back out using FOIL, it is clear that these two lines say the same thing:
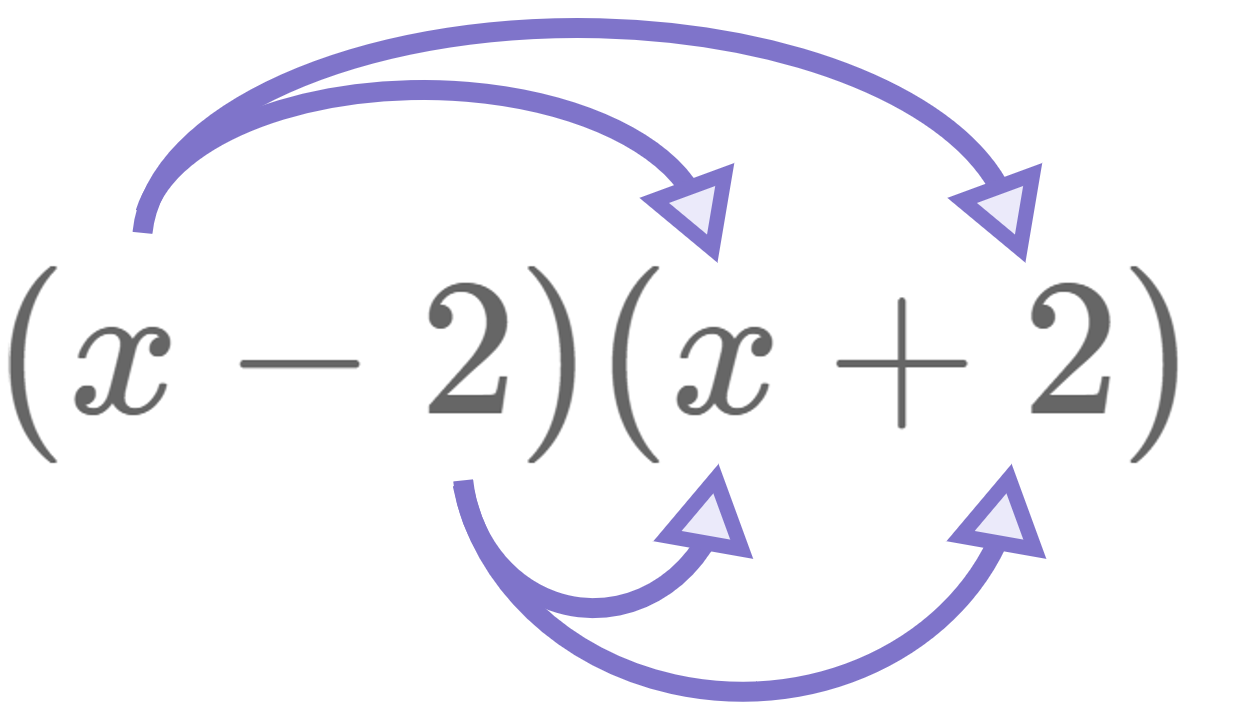
\begin{aligned}&=x^{2}+2x-2x-4 \\[12pt]&=x^{2}-4\end{aligned}
Once again, factorising has resulted in a product of two terms equal to 0. The only possible way that the product of (x-2) and (x+2) can be 0 is if either:
\begin{aligned}(x-2)=0 \text{or} (x+2)=0\end{aligned}
Both of these simpler equations can be solved to give the roots of the quadratic:
\begin{aligned}x-2&=0 \\[6pt]x&=2 \\[20pt]x+2&=0 \\[6pt]x&=-2\end{aligned}
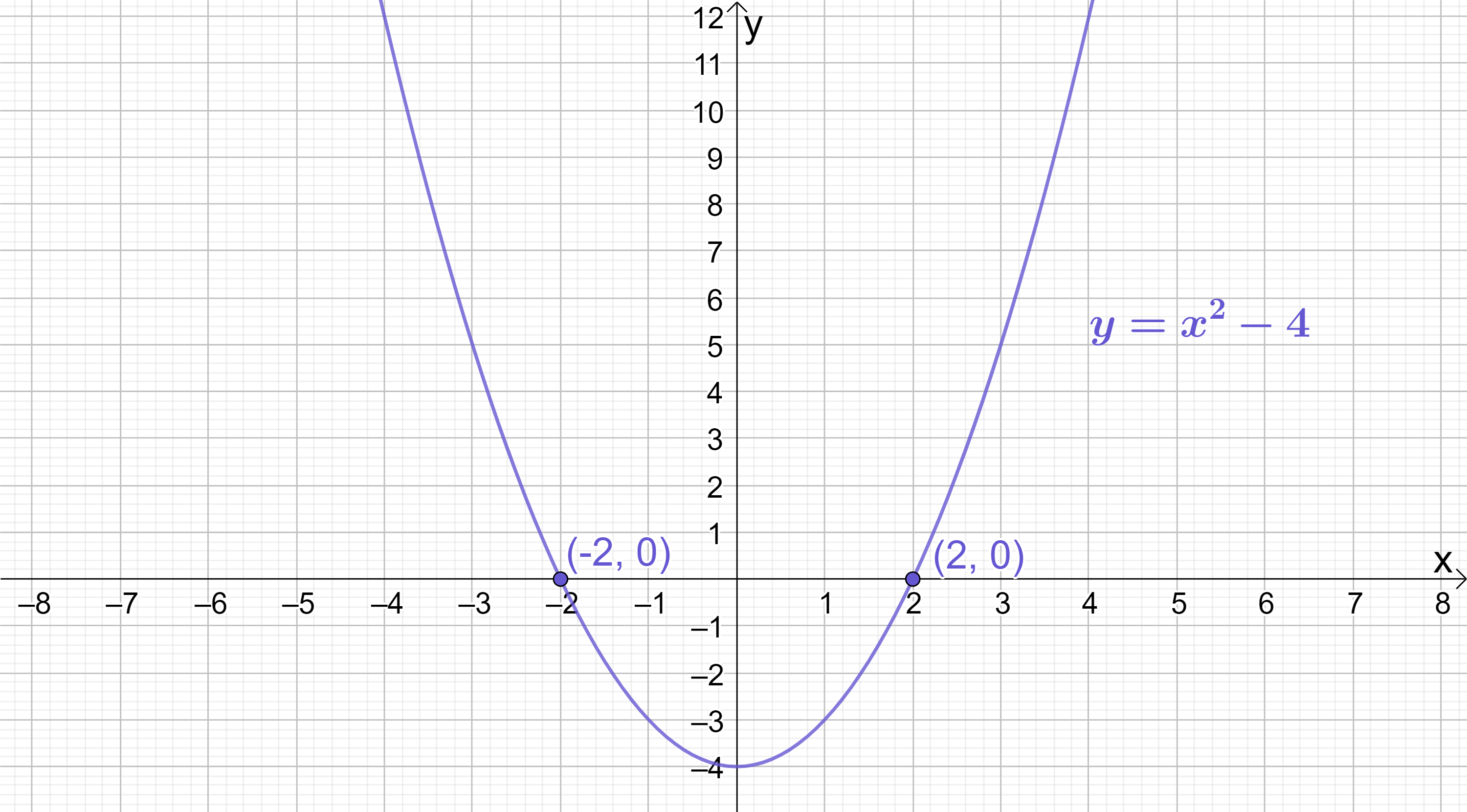
In summary, using factorisation by difference of two squares we have calculated that the quadratic y=x^{2}-4 has roots at (-2, 0) and (2, 0) (remember: at the x-intercepts of any function, y always equals 0).
Sketching y=x^{2}-4 confirms that the roots do indeed lie at (-2, 0) and (2, 0):
Trinomial (Double Brackets)
A “trinomial” is basically just a fancy word for factorising an expression into double brackets. We went into great detail on how to do this in the “Factorising into double brackets” topic in the Double Brackets module, so refer back to that if you’re unsure. This is the most common type of factorisation you will come up against in quadratics, so it’s important to be very comfortable with this technique.
Suppose this time the quadratic in question was y=x^{2}+7x+6. As always, if we are trying to find the roots we should substitute y=0 into the equation and solve. Doing this gives:
\begin{aligned}x^{2}+7x+6=0\end{aligned}
This time, there are no common factors to pull out, and this is clearly not a case that meets the difference of two squares criteria. Therefore, we use trinomials.
Factorising a quadratic like this into two brackets requires some careful thinking. The quadratic in question can be factorised as follows:
\begin{aligned}x^{2}+7x+6&=0 \\[12pt](x+1)(x+6)&=0\end{aligned}
Once again, factorising has resulted in a product of two terms equal to 0. The only possible way that the product of (x+1) and (x+6) can be 0 is if either:
\begin{aligned}(x+1)=0 \text{or} (x+6)=0\end{aligned}
Both of these simpler equations can be solved to give the roots of the quadratic:
\begin{aligned}x+1&=0 \\[6pt]x&=-1 \\[20pt]x+6&=0 \\[6pt]x&=-6\end{aligned}
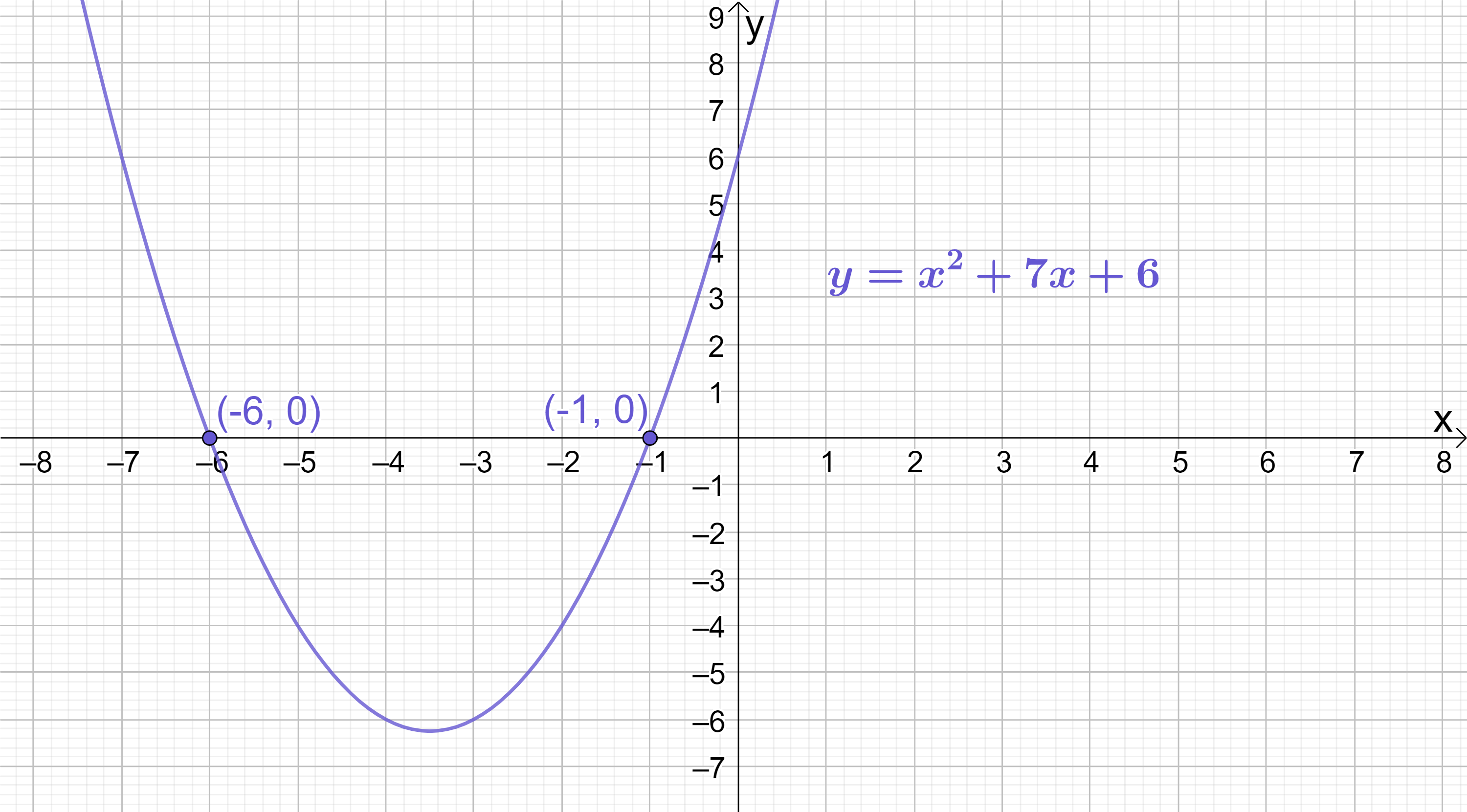
In summary, using factorisation by trinomial we have calculated that the quadratic y=x^{2}+7x+6 has roots at (-1, 0) and (-6, 0) (remember: at the x-intercepts of any function, y always equals 0).
Sketching y=x^{2}+7x+6 confirms that the roots do indeed lie at (-1, 0) and (-6, 0):
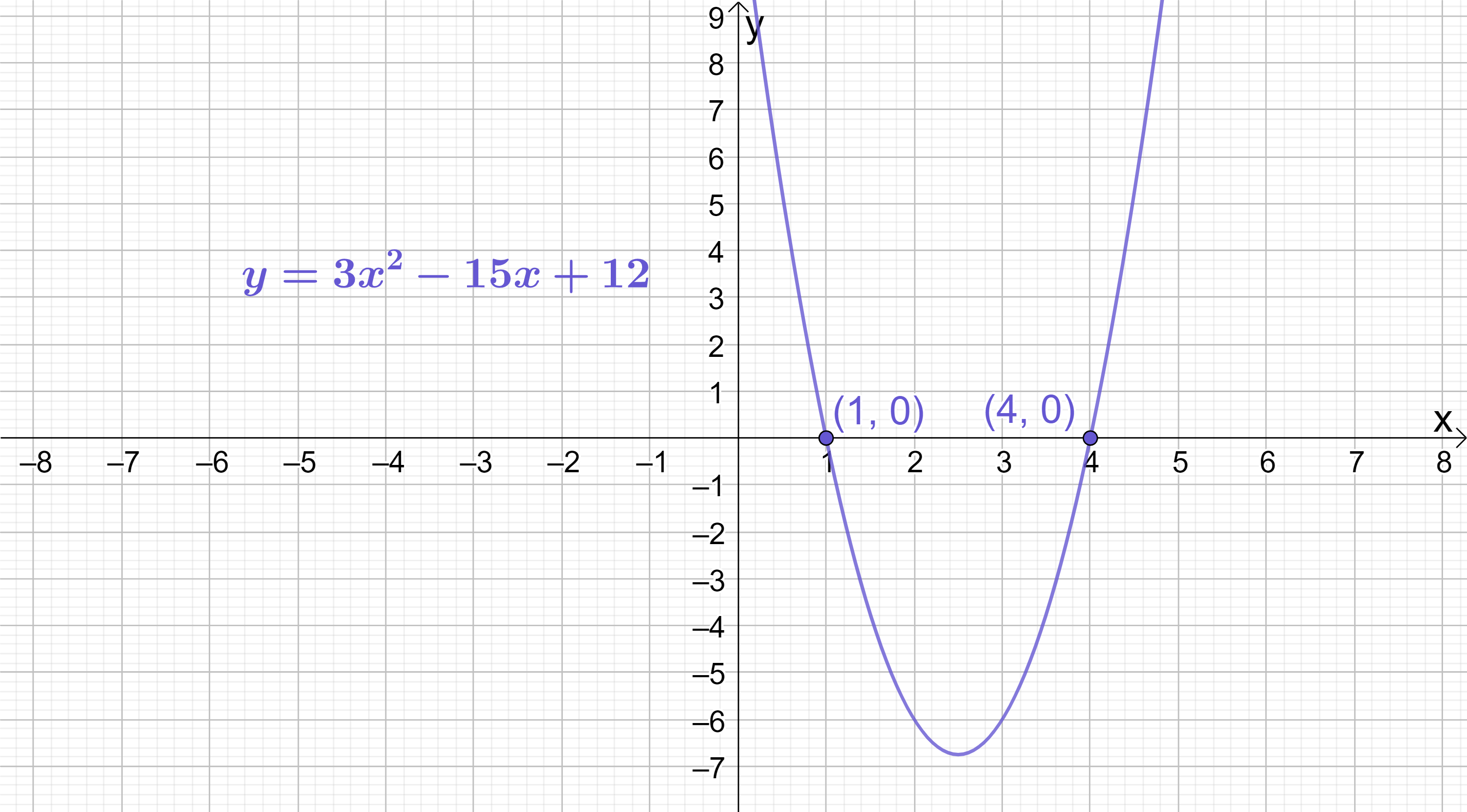
It’s worth looking at a second, slightly more complex example. Suppose this time the quadratic in question was y=3x^{2}-15x+12. As always, if we are trying to find the roots we should substitute y=0 into the equation and solve. Doing this gives:
\begin{aligned}3x^{2}-15x+12=0\end{aligned}
Which can be factorised as follows:
\begin{aligned}(3x-12)(x-1)=0\end{aligned}
Once again, factorising has resulted in a product of two terms equal to 0. The only possible way that the product of (3x-12) and (x-1) can be 0 is if either:
\begin{aligned}(3x-12)=0 \text{or} (x-1)=0\end{aligned}
Both of these simpler equations can be solved to give the roots of the quadratic:
\begin{aligned}3x-12&=0 \\[6pt]3x&=12 \\[6pt]x&=4 \\[20pt]x-1&=0 \\[6pt]x&=1\end{aligned}
In summary, using factorisation by trinomial we have calculated that the quadratic y=3x^{2}-15x+12 has roots at (1, 0) and (4, 0) (remember: at the x-intercepts of any function, y always equals 0).
Sketching y=3x^{2}-15x+12 confirms that the roots do indeed lie at (1, 0) and (4, 0):
Key Outcomes
Factorising is a technique that can be used to calculate the roots (x-intercepts) of quadratic functions.
Factorising turns sums into products. This is useful as it can lead to cancellations or simplified expressions with less variables which are easier to solve.
The only possible way that a\times b=0 can be true is if either: a=0, b=0 or both a & b=0.
When factorising quadratics, there are three possible methods of factorisation you may need:
1) Common factor
2) Difference of two squares
3) Trinomial (double brackets)
If it is possible to pull out a common factor, you should always do so. Sometimes factorisation by common factor is all you will have to do, but in other cases you will have to pull out a common first before factorising further using one of the other methods.
It should always be extremely easy to spot when the difference of two squares technique is required as the quadratic will:
- only have two terms;
- both of the terms will be square numbers; and
- the terms will be subtracting from one another.
To factorise using the difference of two squares, split the quadratic into two brackets: the first bracket will be the the square root of the first term minus the square root of the second term; the second bracket will be the square root of the first term plus the square root of the second term.
If you have ruled out factorisation by common factor and difference of two squares, only then use trinomials.
Factorisation by trinomial is the most common type of factorisation you will come up against in quadratics, so it’s important to be very comfortable with this technique.
Since roots are actual locations (or points) on a graph, once you have found the roots always state them in full (x, y) coordinate form (remember, the y coordinate of a root is always 0).






