Discriminant (Nature of Roots)
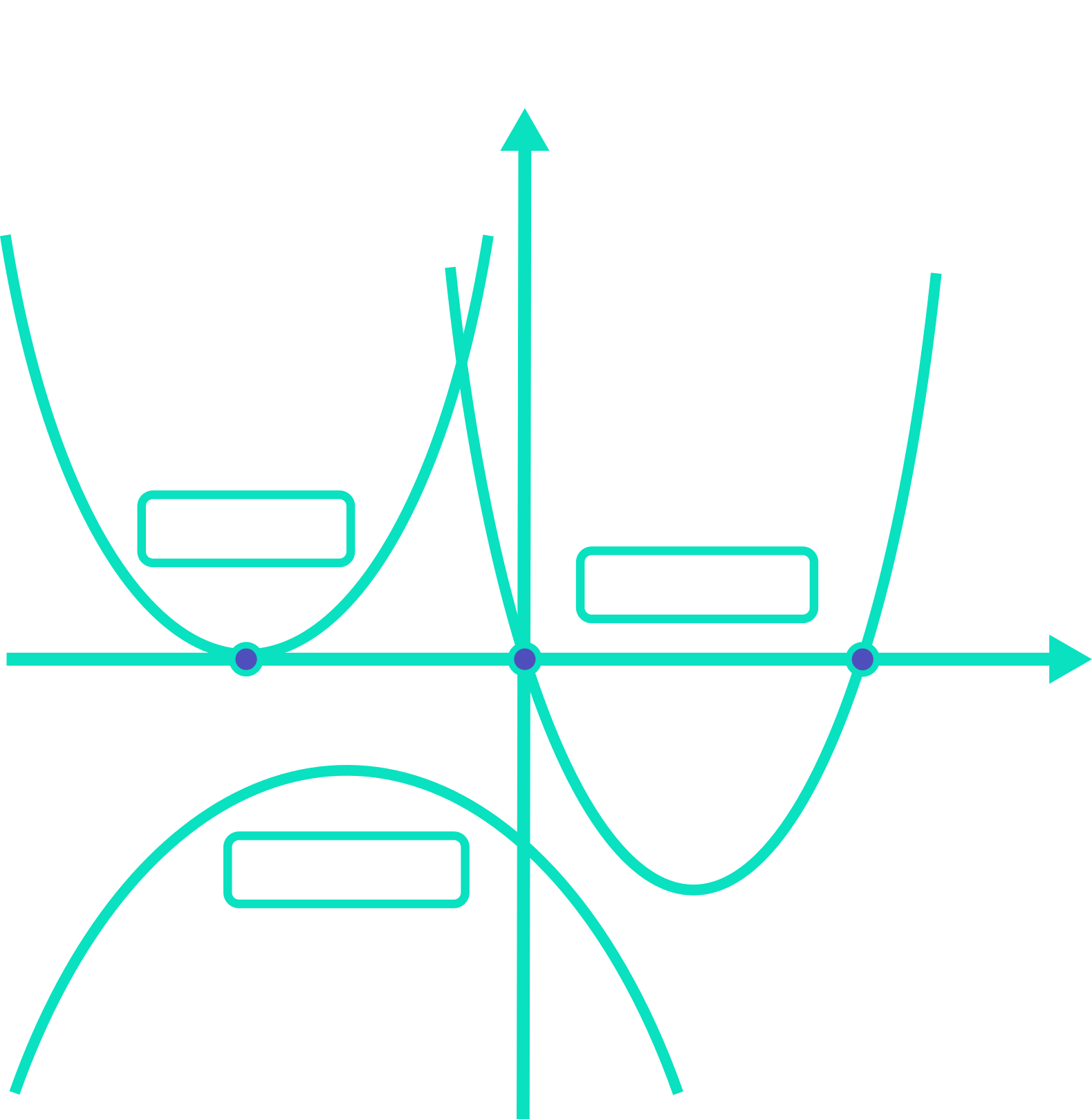
Recall that while a quadratic only ever has one y-intercept, it is possible for a quadratic to have either 2, 1 or 0 roots (i.e. x-intercepts):
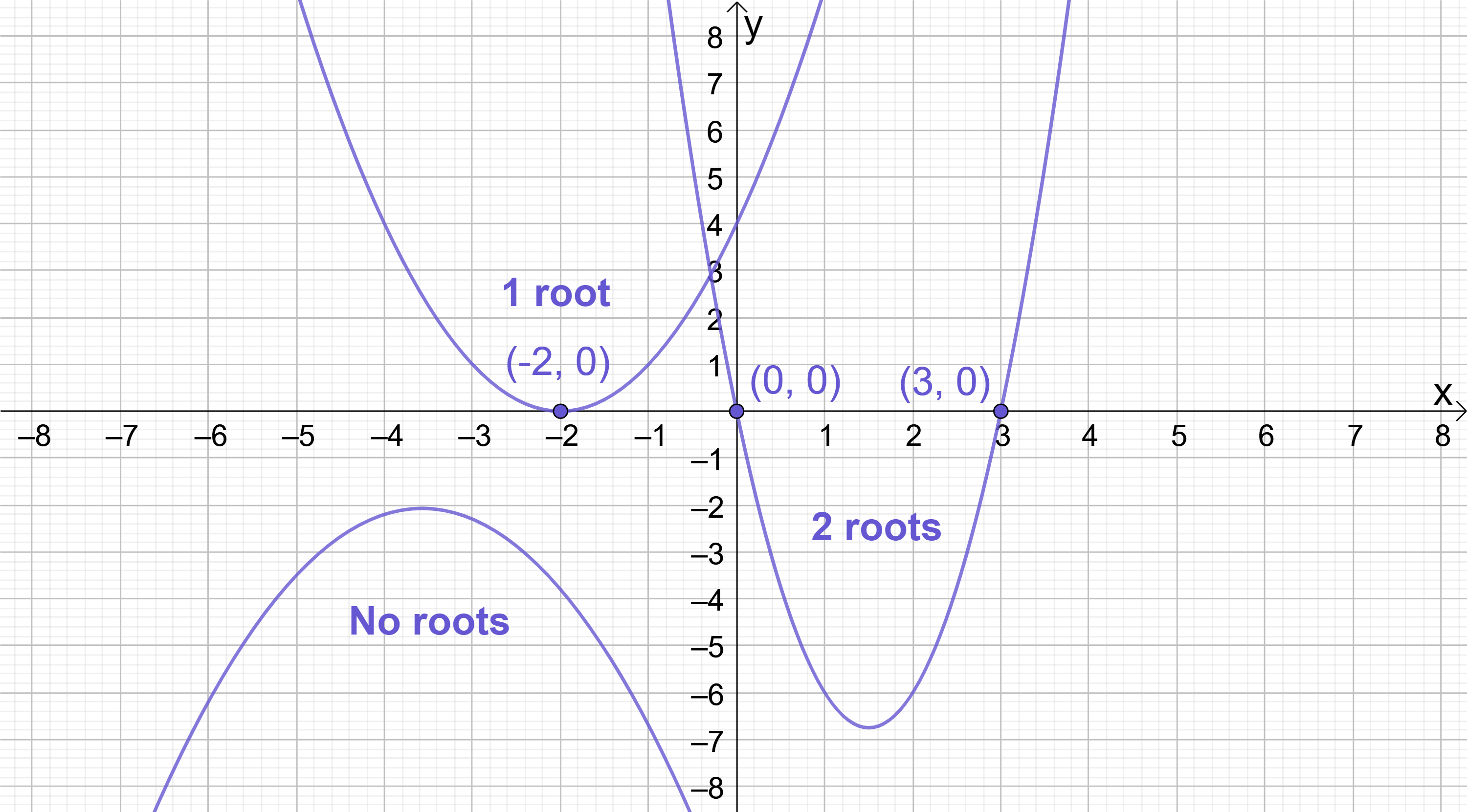
With the benefit of a sketch it is obvious whether a quadratic has 2, 1 or 0 roots, but without a sketch it is not immediately clear. Fortunately, there is a formula which helps us determine how many roots a quadratic has:
The discriminant is a formula which can be used to determine whether a quadratic has 2, 1 or 0 roots. The discriminant is:
\begin{aligned}\boldsymbol{b^{2}-4ac}\end{aligned}
Where \boldsymbol{a}, \boldsymbol{b} and \boldsymbol{c} are the coefficients of any quadratic written in the form of the General Equation \boldsymbol{y=ax^{2}+bx+c}.
On calculating the discriminant, there are three possible outcomes and each outcome relates to one of the three root scenarios (i.e. 2, 1 or 0 roots):
\begin{aligned}\boldsymbol{b^{2}-4ac<0} &\boldsymbol{\rightarrow} \textbf{No real roots} \\[12pt]\boldsymbol{b^{2}-4ac=0} &\boldsymbol{\rightarrow} \textbf{1 real root repeated} \\[12pt]\boldsymbol{b^{2}-4ac>0} &\boldsymbol{\rightarrow} \textbf{2 real distinct roots}\end{aligned}
You should recognise that the discriminant \boldsymbol{b^{2}-4ac} is just a small part of the Quadratic Formula we met in the previous topic:
\begin{aligned}x=\frac{-b\pm\sqrt{\boldsymbol{b^{2}-4ac}}}{2a}\end{aligned}
You already know that the Quadratic Formula is used to calculate the roots of quadratic functions, but the b^{2}-4ac piece of this formula is what dictates whether there will be 2, 1 or 0 roots. Let’s look at each b^{2}-4ac possibility in turn to understand how this affects the roots:
\boldsymbol{b^{2}-4ac<0} \boldsymbol{\rightarrow} \textbf{No real roots}
When the discriminant is negative (i.e. less than zero, <0), the quadratic has no real roots. As an example, let’s take the quadratic y=x^{2}+2x+3 which has coefficients a=1, b=2 and c=3. In this case, the discriminant would be:
\begin{aligned}b^{2}-4ac&=(2)^{2}-4(1)(3) \\[12pt]&=4-12 \\[12pt]&=-8\end{aligned}
Since -8<0, according to the rule this quadratic should have no real roots. But how do we know if this is true or not? Well, we could try to calculate the roots of this quadratic using the Quadratic Formula and see what happens:
\begin{aligned}x&=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a} \\[12pt]x&=\frac{-(2)\pm\sqrt{(2)^{2}-4(1)(3)}}{2(1)} \\[12pt]x&=\frac{-2\pm\sqrt{4-12}}{2} \\[12pt]x&=\frac{-2\pm\sqrt{-8}}{2}\end{aligned}
Normally at this stage we would split the formula into the two scenarios (one using + and one using -), but this time we have a problem.
The discriminant, b^{2}-4ac, has worked out as -8, and in the Quadratic Formula the discriminant always sits under a square root (\sqrt{}). But recall from the Surds and Indices chapter that you cannot take the square root of a negative number as this gives a maths error (try \sqrt{-8} in your calculator).
Basically, we’re stuck! We’ve tried to use the Quadratic Formula to calculate the roots of this quadratic and it’s not that the formula has given us a wrong answer, but more interestingly, it’s not been able to give us any answer at all! The formula has completely “broken down” and led to a maths error.
This error tells us something important. The Quadratic Formula, which we use to find the roots of quadratic functions, has broken down in this case because we have asked it to do something impossible – we have asked it to find roots that don’t exist!
If we sketch y=x^{2}+2x+3, this confirms that indeed this quadratic does not have any real roots (it never touches the x-axis!):
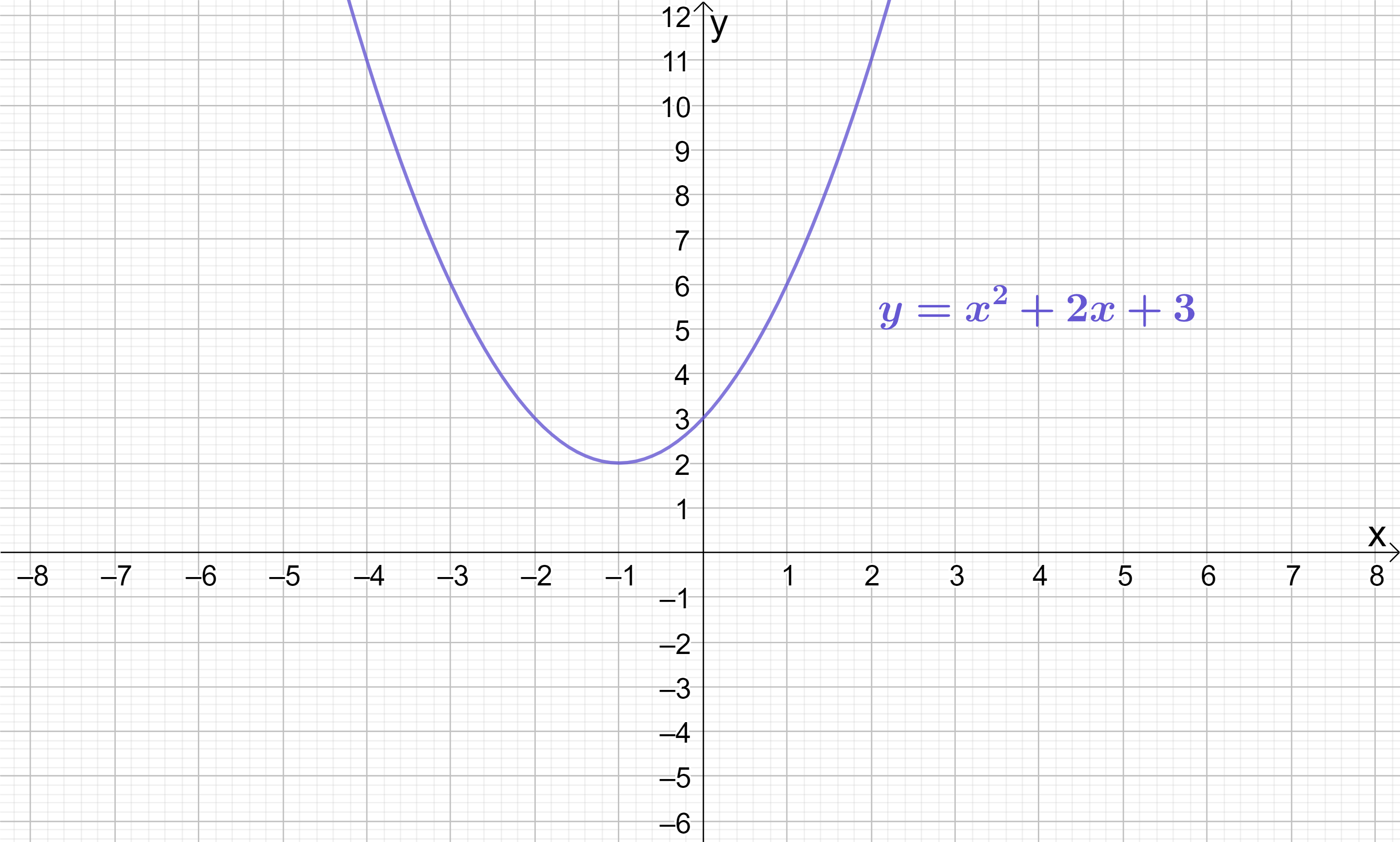
If you think about it, it makes complete sense that the Quadratic Formula “broke down” in this example. The quadratic y=x^{2}+2x+3 clearly does not have roots, therefore finding its roots is impossible, so if you try to calculate them using the Quadratic Formula you will encounter a maths error.
\boldsymbol{b^{2}-4ac=0} \boldsymbol{\rightarrow} \textbf{1 real root repeated}
When the discriminant is equal to zero (=0), the quadratic has real and equal roots. As an example, let’s take the quadratic y=x^{2}+4x+4, which has coefficients a=1, b=4 and c=4. In this case, the discriminant would be:
\begin{aligned}b^{2}-4ac&=(4)^{2}-4(1)(4) \\[12pt]&=16-16 \\[12pt]&=0\end{aligned}
Since b^{2}-4ac=0, according to the rule this quadratic should have 1 real root repeated. Once again, to determine whether this is true or not we could try to calculate the roots of this quadratic using the Quadratic Formula and see what happens:
\begin{aligned}x&=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a} \\[12pt]x&=\frac{-(4)\pm\sqrt{(4)^{2}-4(1)(4)}}{2(1)} \\[12pt]x&=\frac{-4\pm\sqrt{16-16}}{2} \\[12pt]x&=\frac{-4\pm\sqrt{0}}{2}\end{aligned}
And splitting into the + case and the - case, we have:
\begin{aligned}x&=\frac{-4+\sqrt{0}}{2} &\text{or} x&=\frac{-4-\sqrt{0}}{2} \\[12pt]x&=\frac{-4}{2} &\text{or} x&=\frac{-4}{2} \\[12pt]x&=-2 &\text{or} x&=-2\end{aligned}
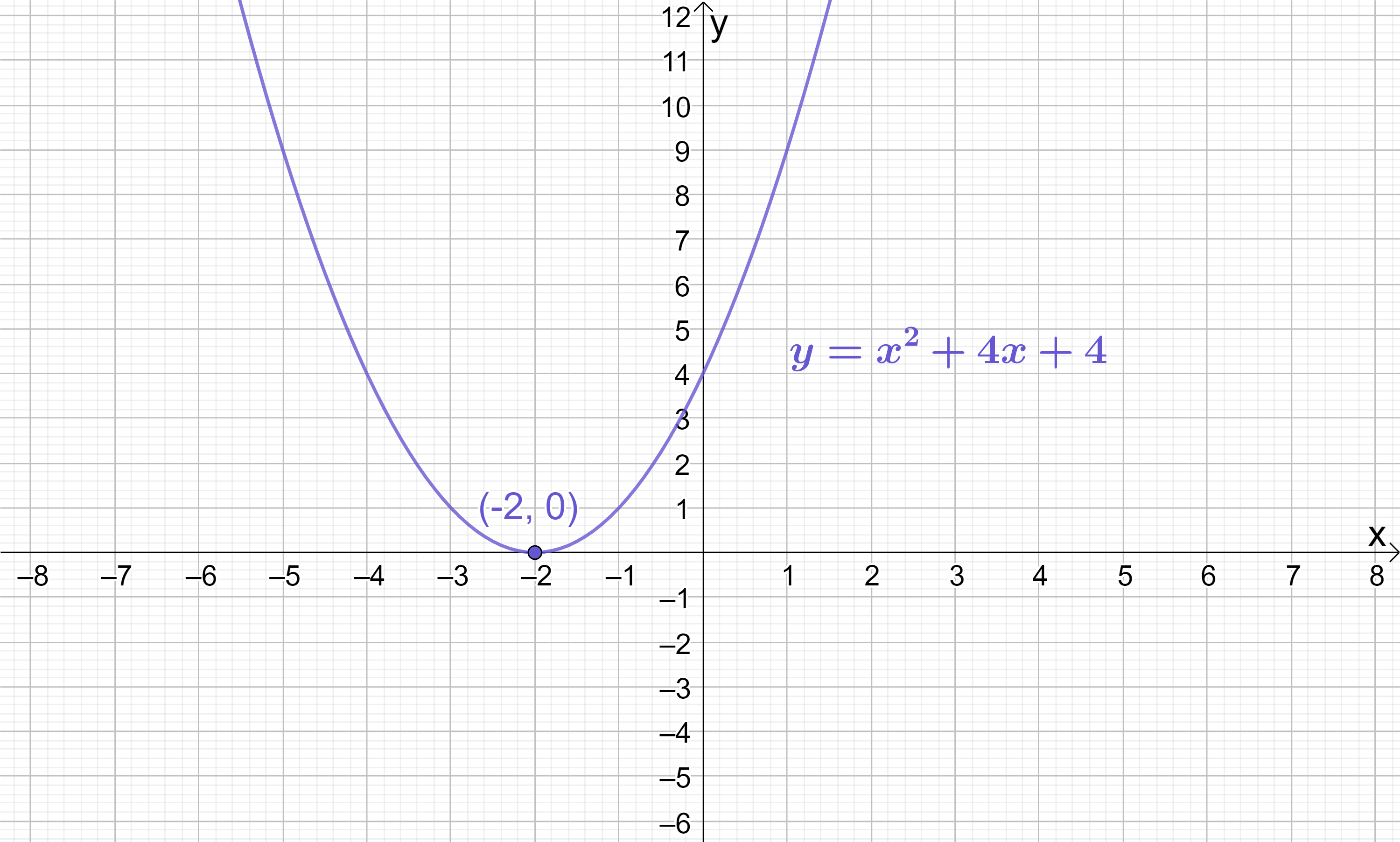
Hence the quadratic y=x^{2}+4x+4 has only 1 root (repeated) at (-2, 0).
This hopefully makes it clear why we use the terminology “1 real root repeated”. Since the discriminant worked out to be 0, when we split the Quadratic Formula out into the two scenarios as usual:
\begin{aligned}x&=\frac{-4+\sqrt{0}}{2} &\text{or} x&=\frac{-4-\sqrt{0}}{2}\end{aligned}
Did it make any difference that in one scenario we were adding \sqrt{0} to the numerator, whilst in the other we were subtracting \sqrt{0} from the numerator? Of course not, since \sqrt{0}=0 and adding or subtracting 0 makes no difference! Hence both scenarios led to the same answer (the repeated solution) of x=-2.
If we sketch y=x^{2}+4x+4, this confirms that indeed this quadratic has only one root (it only touches the x-axis once) at (-2, 0):
The following example is typical of how this knowledge might be challenged in your exam:
Example 1
The quadratic y=x^{2}+qx+25 has one real root. Find the two values of q.
Comparing y=x^{2}+qx+25 to the General Equation:
\begin{aligned}y&=x^{2}+qx+25 \\[12pt]y&=ax^{2}+bx+c\end{aligned}
We see that we don’t know the values of all the coefficients – up till now we have always had this information. In this case, a=1 and c=25, but b – the coefficient in front of the x term – is actually b=q. We don’t have a numerical value for b, but this is fine – we can still substitute b=q as if it were a normal numerical value.
We have been told y=x^{2}+qx+25 has one real root, so therefore we know:
\begin{aligned}b^{2}-4ac=0\end{aligned}
Substituting a=1, b=q and c=25 gives:
\begin{aligned}b^{2}-4ac&=0 \\[12pt](q)^{2}-4(1)(25)&=0 \\[12pt]q^{2}-100&=0 \\[12pt]q^{2}&=100 \\[12pt]q&=\sqrt{100} \\[12pt]q&=\pm10\end{aligned}
In the last step it’s easy to forget that q=\sqrt{100} has two solutions: q=10 and q=-10 (since 10\times10=100 but equally -10\times-10=100). Watch out for this whenever you’re working with square roots at the National 5 level – all square roots have two solutions (although there are times where it may be appropriate to discard one of them, but this example did specifically ask for two values of q).
\boldsymbol{b^{2}-4ac>0} \boldsymbol{\rightarrow} \textbf{2 real distinct roots}
When the discriminant is positive (i.e. greater than zero, >0), the quadratic has two real and distinctly different roots. This is the most common type of quadratic you will encounter. As an example, let’s take the quadratic y=x^{2}+2x-8, which has coefficients a=1, b=2 and c=-8. In this case, the discriminant would be:
\begin{aligned}b^{2}-4ac&=(2)^{2}-4(1)(-8) \\[12pt]&=4+32 \\[12pt]&=36\end{aligned}
Since 36>0, according to the rule this quadratic should have 2 real and distinct roots. As before, to determine whether this is true or not we could try to calculate the roots of this quadratic using the Quadratic Formula and see what happens:
\begin{aligned}x&=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a} \\[12pt]x&=\frac{-(2)\pm\sqrt{(2)^{2}-4(1)(-8)}}{2(1)} \\[12pt]x&=\frac{-2\pm\sqrt{4+32}}{2} \\[12pt]x&=\frac{-2\pm\sqrt{36}}{2}\end{aligned}
And splitting into the + case and the - case, we have:
\begin{aligned}x&=\frac{-2+\sqrt{36}}{2} &\text{or} x&=\frac{-2-\sqrt{36}}{2} \\[12pt]x&=\frac{-2+6}{2} &\text{or} x&=\frac{-2-6}{2} \\[12pt]x&=\frac{4}{2} &\text{or} x&=\frac{-8}{2} \\[12pt]x&=2 &\text{or} x&=-4\end{aligned}
Hence the quadratic y=x^{2}+2x-8 has 2 distinct roots at (-4, 0) and (2, 0).
Hopefully this case seems pretty straightforward to you. Since the discriminant worked out to be 36, when we split the Quadratic Formula out into the two scenarios as usual:
\begin{aligned}x&=\frac{-2+\sqrt{36}}{2} &\text{or} x&=\frac{-2-\sqrt{36}}{2}\end{aligned}
Obviously, it makes a big difference that in one scenario we were adding \sqrt{36} (i.e. 6) to the numerator, whilst in the other we were subtracting \sqrt{36} from the numerator. Clearly the two were never going to work out to be the same. Hence the roots are called real and distinct because the roots have two different values and therefore lie at different places.
If we sketch y=x^{2}+2x-8, this confirms that indeed this quadratic has 2 real and distinct roots at (-4, 0) and (2, 0):
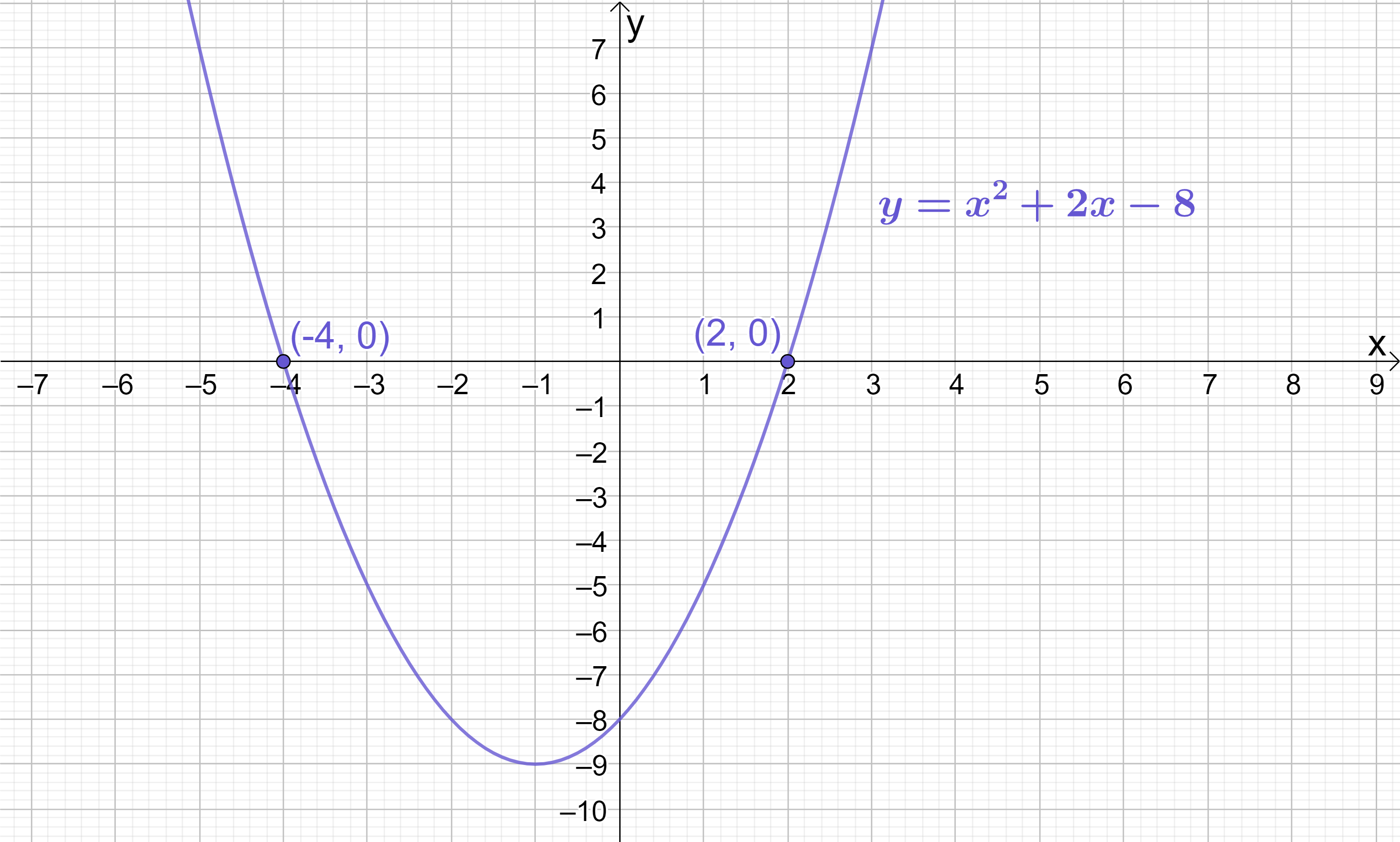
The following example is typical of how this knowledge might be challenged in your exam:
Example 2
The quadratic y=px^{2}-4x+1 has two real roots. Find the range of values of p.
Comparing y=px^{2}-4x+1 to the General Equation:
\begin{aligned}y&=px^{2}-4x+1 \\[12pt]y&=ax^{2}+bx+c\end{aligned}
Again, we don’t know the values of all the coefficients. In this case, b=-4 and c=1, but a – the coefficient in front of the x^{2} term – is actually a=p. We don’t have a numerical value for a, but this is fine – we can still substitute a=p as if it were a normal numerical value.
We have been told y=px^{2}-4x+1 has two real roots, so therefore we know:
\begin{aligned}b^{2}-4ac>0\end{aligned}
Substituting a=p, b=-4 and c=1 gives:
\begin{aligned}b^{2}-4ac&>0 \\[12pt](-4)^{2}-4(p)(1)&>0 \\[12pt]16-4p&>0 \\[12pt]16&>4p \\[12pt]4p&<16 \\[12pt]p&<4\end{aligned}
Notice the question does not ask us to find the value of p, but a range of values of p. This is because there are many possible values of p that will all result in this quadratic having a discriminant greater than zero, and therefore, two real and distinct roots. Our solution, p<4, is exactly this – it is not a specific value, but a range (i.e. p can be any value less than 4).
Let’s test a few random values of p that are less than 4 to convince ourselves that our range is correct. Suppose we let p=2, then with a=p=2, b=-4 and c=1 we have:
\begin{aligned}b^{2}-4ac&=(-4)^{2}-4(2)(1) \\[12pt]&=16-8 \\[12pt]&=8>0\end{aligned}
With p=2, the discriminant is greater than zero as predicted.
This time, let’s try p=-3. With a=p=-3, b=-4 and c=1 we have:
\begin{aligned}b^{2}-4ac&=(-4)^{2}-4(-3)(1) \\[12pt]&=16+12 \\[12pt]&=28>0\end{aligned}
With p=-3, the discriminant is greater than zero as predicted.
These are only two random exampes, but any value of p less than 4 will work (try a few yourself).
What if we tried a value of p greater than 4? What would happen then? Let’s try p=6. We have a=p=6, b=-4 and c=1:
\begin{aligned}b^{2}-4ac&=(-4)^{2}-4(6)(1) \\[12pt]&=16-24 \\[12pt]&=-8<0\end{aligned}
With p=6, the discriminant is less than zero which is incorrect as this would imply the quadratic has no real roots (when we were told in the question that it has two real roots!)
Key Outcomes
The discriminant is a formula which can be used to determine whether a quadratic has 2, 1 or 0 roots. The discriminant is:
\begin{aligned}b^{2}-4ac\end{aligned}
Where a, b and c are the coefficients of any quadratic written in the form of the General Equation y=ax^{2}+bx+c.
On calculating the discriminant, there are three possible outcomes and each outcome relates to one of the three root scenarios (i.e. 2, 1 or 0 roots):
\begin{aligned}b^{2}-4ac<0 &\boldsymbol{\rightarrow} \text{No real roots} \\[12pt]b^{2}-4ac=0 &\boldsymbol{\rightarrow} \text{1 real root repeated} \\[12pt]b^{2}-4ac>0 &\boldsymbol{\rightarrow} \text{2 real distinct roots}\end{aligned}