What is Compounding?
The simplest way for you to grasp the idea behind compounding is for us to walk through a real life scenario together.
Suppose you buy a home worth £100,000. The prospects for your area are good, so the home is expected to grow in value at 4% per year. What is the expected valuation of your home after:
a) 1 year?
b) 4 years?
a) Recall that if you are increasing a quantity by a certain percentage, then the new total percentage must be greater than 100%.
If the price has to increase by 4% per year, then the new price after one year will be the original price (100%) plus a 4% increase, for a total of 104% (i.e. we need to multiply by 1.04):
\begin{aligned}\text{Value}\ Y_{1}&=\text{Original price}\times 1.04 \\[12pt]&=£100,000\times 1.04 \\[12pt]&=£104,000\end{aligned}
b) To arrive at the valuation after 4 years, we need to increase the price by a further 4% for each of the next 3 years. However, notice that this time we do not start with the original £100,000 price since the value has already grown to £104,000 after the first year:
\begin{aligned}\text{Value}\ Y_{2}&=\text{Value}\ Y_{1}\times 1.04 \\[12pt]&=£104,000\times 1.04 \\[12pt]&=£108,160\end{aligned}
\begin{aligned}\text{Value}\ Y_{3}&=\text{Value}\ Y_{2}\times 1.04 \\[12pt]&=£108,160\times 1.04 \\[12pt]&=£112,486\end{aligned}
\begin{aligned}\text{Value}\ Y_{4}&=\text{Value}\ Y_{3}\times 1.04 \\[12pt]&=£112,486\times 1.04 \\[12pt]&=£116,985\end{aligned}
A: The value of the home after 4 years has increased by £16,985, growing to £116,985.
Overall, by growing in value at 4% per year, the valuations of the house for each of the years were as follows:
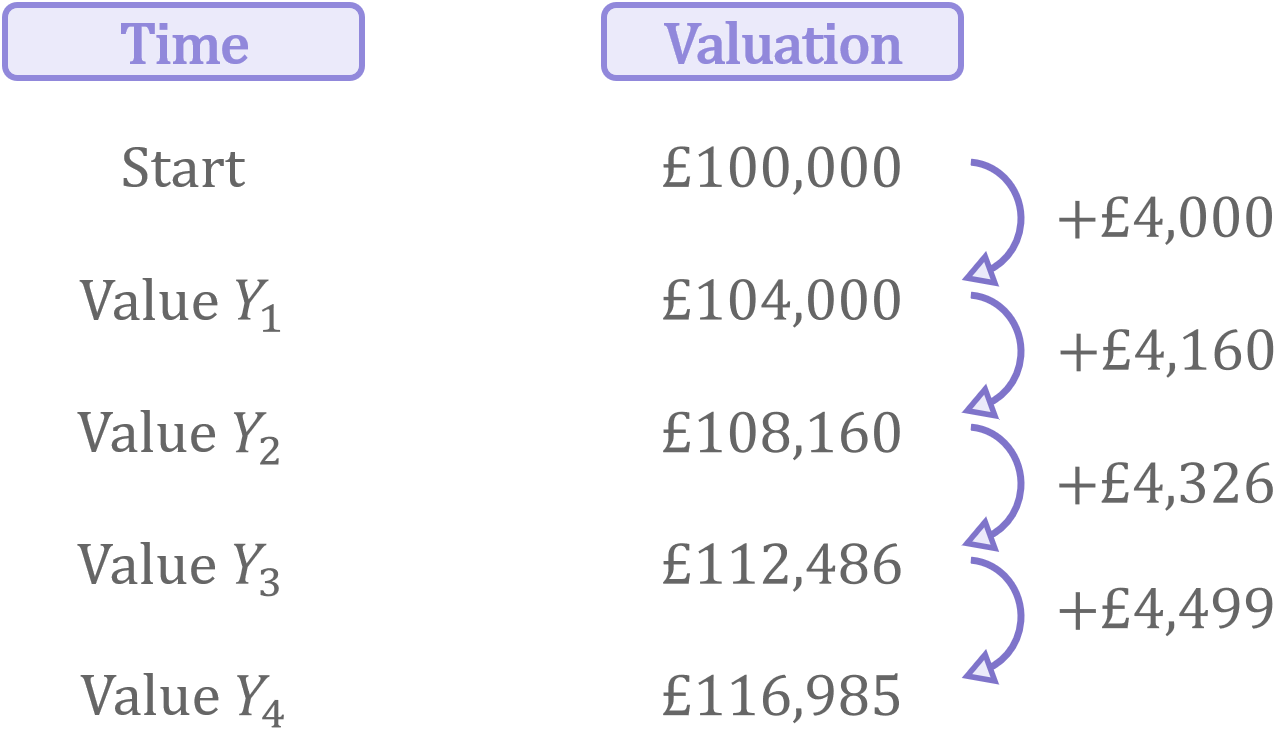
Notice that in each subsequent year, the valuation increases by more than it did in the previous year. How has this happened, given the growth rate was held constant at 4% each year?
This is an effect known as compounding. The valuation increases more rapidly in each subsequent year because the gains made in the prior year make gains of their own the following year. So, because you have a higher starting valuation in each subsequent year, applying the same 4% growth rate to a higher starting valuation causes the valuation to jump up by a greater amount each time.
This was an example of compound appreciation. When something appreciates, it grows in value. A different example may have seen the value of the house fall; when something falls in value, this is called depreciation.
In the example above, between parts (a) and (b) we ultimately performed four separate calculations to arrive at the value of the home after 4 years. This was fairly time consuming, but can you imagine how time consuming it would be if we had to work out the value after say 15 years? (15 separate calculations) Or even 30 years? (30 separate calculations!)
Fortunately, there is a shortcut for performing this type of compounding calculation. If we analyse what we actually did to get to our valuation after four years, we see that:
We took the initial price and increased it by 4% to get the value after 1 year:
\begin{aligned}\text{Value}\ Y_{1}&=\text{Original price}\times 1.04 \\[12pt]&=£104,000\end{aligned}
We took the result of that calculation and increased that by 4% to get the value after year 2:
\begin{aligned}\text{Value}\ Y_{2}&=\text{Value}\ Y_{1}\times 1.04 \\[12pt]&=(\text{Original price}\times 1.04)\times 1.04 \\[12pt]&=£108,160\end{aligned}
We took the result of that calculation and increased that by 4% to get the value after year 3:
\begin{aligned}\text{Value}\ Y_{3}&=\text{Value}\ Y_{2}\times 1.04 \\[12pt]&=((\text{Original price}\times 1.04)\times 1.04)\times 1.04 \\[12pt]&=£112,486\end{aligned}
And finally, we took the result of that calculation and increased that by 4% one last time to get the value after year 4:
\begin{aligned}\text{Value}\ Y_{4}&=\text{Value}\ Y_{3}\times 1.04 \\[12pt]&=(((\text{Original price}\times 1.04)\times 1.04)\times 1.04)\times 1.04 \\[12pt]&=£116,985\end{aligned}
In the end, the value after 4 years was achieved simply by taking the initial price and multiplying it by 1.04 four separate times:
\begin{aligned}\text{Value}\ Y_{4}&=\text{Original price}\times 1.04\times 1.04\times 1.04\times 1.04 \\[12pt]&=£116,985\end{aligned}
Since this is just a series of multiplications, the order in which we calculate them does not matter – we do not need to calculate them in order going from left to right. For example:
\begin{aligned}2\times3\times4&=24 \\[6pt]2\times4\times3&=24 \\[6pt]3\times2\times4&=24 \\[6pt]3\times4\times2&=24 \\[6pt]4\times2\times3&=24 \\[6pt]4\times3\times2&=24\end{aligned}
You can see that changing the order of the numbers does not matter if we are simply multiplying them. The result is always the same.
So, when calculating our value in year 4, it can be made simpler if we first consider all the 1.04 multiples first. Since:
\begin{aligned}1.04\times1.04&=(1.04)^{2}=1.0816 \\[6pt]1.04\times1.04\times1.04&=(1.04)^{3}=1.12486 \\[6pt]1.04\times1.04\times1.04\times1.04&=(1.04)^{4}=1.16985\end{aligned}
We can write our equation in a much more condensed format:
\begin{aligned}\text{Value}\ Y_{4}&=\text{Original price}\times 1.04\times 1.04\times 1.04\times 1.04 \\[12pt]&=\text{Original price}\times (1.04)^{4} \\[12pt]&=£100,000\times 1.16985 \\[12pt]&=£116,985\end{aligned}
With this new knowledge, if we had actually been asked to calculate the house’s value after 30 years, assuming continued 4% growth per year, then we wouldn’t have to do 30 separate calculations anymore; instead we can find the answer with one straightforward calculation:
\begin{aligned}\text{Value}\ Y_{30}&=\text{Original price}\times (1.04)^{30} \\[12pt]&=£100,000\times 3.24340 \\[12pt]&=£324,340\end{aligned}
I’m sure you would agree this is a whole lot easier than doing 30 separate calculations!
In general, we can tackle compounding questions with two standard formulae:
For appreciation questions:
\begin{aligned}\boldsymbol{\textbf{Value}_{n}=\textbf{Original value}\times {(1+app\ \%)}^{n}}\end{aligned}
For depreciation questions:
\begin{aligned}\boldsymbol{\textbf{Value}_{n}=\textbf{Original value}\times {(1-dep\ \%)}^{n}}\end{aligned}
Where:
– \boldsymbol{\textbf{Value}_{n}} is the value after \boldsymbol{n} periods;
– \boldsymbol{app\ \%} is the rate of appreciation (e.g. in our house example, this was a appreciation rate of 4% per year);
– \boldsymbol{dep\ \%} is the rate of depreciation (for example, a car falling in value at 15% per year); and
– \boldsymbol{n} is the number of periods over which the quantity is appreciating or depreciating (e.g. in our house example, this was 4 years, so in that example \boldsymbol{n=4}. Most of the time, \boldsymbol{n} is in units of years (but not always, so be careful with your units!)
Example 1
Mark deposits £5,000 in a bank account which pays 3% compound interest per year. How much interest would be earned over 6 years?
This is an example of compound appreciation (Mark is receiving interest, so his bank balance is growing), so we use the standard formula:
\begin{aligned}\text{Value}_{n}&=\text{Original value}\times(1+app\ \%)^{n}\end{aligned}
We can customise this formula to fit this particular example:
\begin{aligned}\text{Balance}_{n}&=\text{Original balance}\times(1+interest\ \%)^{n} \\[12pt]\text{Balance}_{6}&=£5000\times(1+3\%)^{6} \\[12pt]&=£5000\times(1+0.03)^{6} \\[12pt]&=£5000\times(1.03)^{6} \\[12pt]&=£5000\times1.1940523 \\[12pt]&=£5,970.26\end{aligned}
Calculating the total interest earned (which is what the question actually asks for) is then a simple matter of working out how much Mark’s balance has increased by:
\begin{aligned}\text{Interest earned}&=\text{Balance}_{6}-\text{Original balance} \\[12pt]&=£5,970.26-£5,000 \\[12pt]&=£970.26\end{aligned}
Example 2
Jennifer buys a car for £17,000. The value of this car will experience compound decay (i.e. depreciation) at a rate of 25% per year. Calculate the value of the car after 8 years.
This is an example of compound depreciation (cars almost always fall in value), so we use the standard formula:
\begin{aligned}\text{Value}_{n}&=\text{Original value}\times(1-dep\ \%)^{n}\end{aligned}
We can customise this formula to fit this particular example:
\begin{aligned}\text{Value}_{n}&=\text{Original value}\times(1-decay\ rate)^{n} \\[12pt]\text{Value}_{8}&=£17,000\times(1-25\%)^{8} \\[12pt]&=£17,000\times(1-0.25)^{8} \\[12pt]&=£17,000\times(0.75)^{8} \\[12pt]&=£17,000\times0.1001129 \\[12pt]&=£1,701.92\end{aligned}
Example 3
Baby elephants grow most rapidly in the early years of their development. Their body weight increases by 4% every month for the first 5 years of their lives. Given this, what would an elephant weighing 200kg at birth weigh after 5 years?
This is an example of compound appreciation (the elephant’s weight should increase as it grows up), so we use the standard formula:
\begin{aligned}\text{Value}_{n}&=\text{Original value}\times(1+app\ \%)^{n}\end{aligned}
We can customise this formula to fit this particular example:
\begin{aligned}\text{Weight}_{n}&=\text{Original weight}\times(1+growth\ rate)^{n}\end{aligned}
However, we have to be extremely careful about n – the number of periods – in this example. Recall that we defined n as the number of periods over which the quantity in question is appreciating or depreciating. In this example, the growth rate of the elephant’s weight (4%) has been stated on a monthly basis, not an annual basis. This means that any \boldsymbol{n} value we use in our equation must be in months, not years.
The question asks for the elephant’s weight after 5 years – this is 60 months (5 x 12). We therefore need to ensure our calculation compounds the elephant’s weight over 60 periods, not 5:
\begin{aligned}\text{Weight}_{n}&=\text{Original weight}\times(1+growth\ rate)^{n} \\[12pt]\text{Weight}_{60}&=200\times(1+4\%)^{60} \\[12pt]&=200\times(1+0.04)^{60} \\[12pt]&=200\times(1.04)^{60} \\[12pt]&=200\times10.5196 \\[12pt]&=2,103.92kg\ \text{or}\ 2.1\ \text{tonnes}\end{aligned}
Key Outcomes
When something appreciates, it grows in value.
When something depreciates, it falls in value.
For appreciation questions:
\begin{aligned}\boldsymbol{\textbf{Value}_{n}=\textbf{Original value}\times {(1+app\ \%)}^{n}}\end{aligned}
For depreciation questions:
\begin{aligned}\boldsymbol{\textbf{Value}_{n}=\textbf{Original value}\times {(1-dep\ \%)}^{n}}\end{aligned}
Where:
– \text{Value}_{n} is the value after n periods;
– app\ \% is the rate of appreciation;
– dep\ \% is the rate of depreciation; and
– n is the number of periods over which the quantity is appreciating or depreciating. Most of the time, n is in units of years (but not always, so be careful with your units!)






