Completing the Square
There is a very clear limitation to methods for finding the turning point of a quadratic that rely on knowing the roots of the quadratic – how could you use these methods if the quadratic didn’t have any roots for you to work with? There are plenty of quadratics which don’t have roots, but all quadratics do have a turning point, so there must be a way to find the turning points of these quadratics without using roots!
Completing the Square is a more powerful technique for finding the turning point of a quadratic. Completing the Square works for all quadratics, including those which do not have roots.
By now you are accustomed to working with quadratics which are in the standard form of the General Equation y=ax^{2}+bx+c. When a quadratic is in the form y=ax^{2}+bx+c, you can easily read off both its nature and y-intercept, and you can use factorisation or the Quadratic Formula to find its roots. However, there is no quick way to take a quadratic in the form y=ax^{2}+bx+c and read off its turning point. To figure out the turning point requires a bit more work.
Completing the Square is a process which takes a quadratic in the form of the General Equation:
\boldsymbol{y=ax^{2}+bx+c}
And transforms it into a quadratic of the form:
\boldsymbol{y=(x+p)^{2}+q}
In which the turning point can then easily be extracted as \boldsymbol{(-p, q)}.
Below is a summary of the two forms and the information they each reveal about a specific quadratic:

To transform a quadratic from y=ax^{2}+bx+c form into y=(x+p)^{2}+q form, we Complete the Square.
Before Completing the Square, make sure the \boldsymbol{a} coefficient (the number in front of the \boldsymbol{x^{2}} term) is 1. Only the more complicated examples have a coefficients other that 1 (see example 3 at the end of this topic for an example of this type). When you are ready to Complete the Square, the steps are as follows:
1) Open a bracket and put an \boldsymbol{x} term at the front
2) Add half the \boldsymbol{b} coefficient, then close the bracket and square it
3) Separately, multiply out the new bracket and see what constant you have (in most cases, this will not be the same as the constant the quadratic had in its original form, i.e. the \boldsymbol{c} coefficient)
4) Make an adjustment (add or subtract a number) to ensure the constant ultimately works out the same as the original \boldsymbol{c} coefficient
5) Once the quadratic is in \boldsymbol{y=(x+p)^{2}+q} form, extract the turning point as \boldsymbol{(-p, q)}
This process is best illustrated with a detailed worked example.
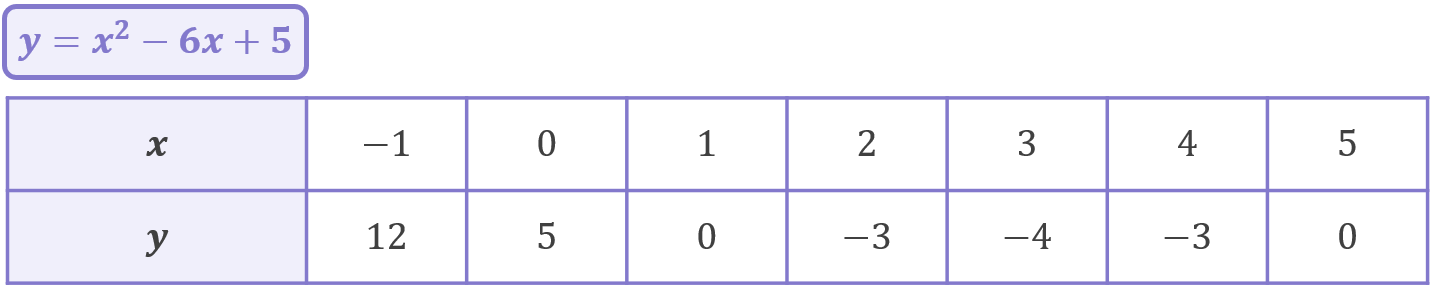
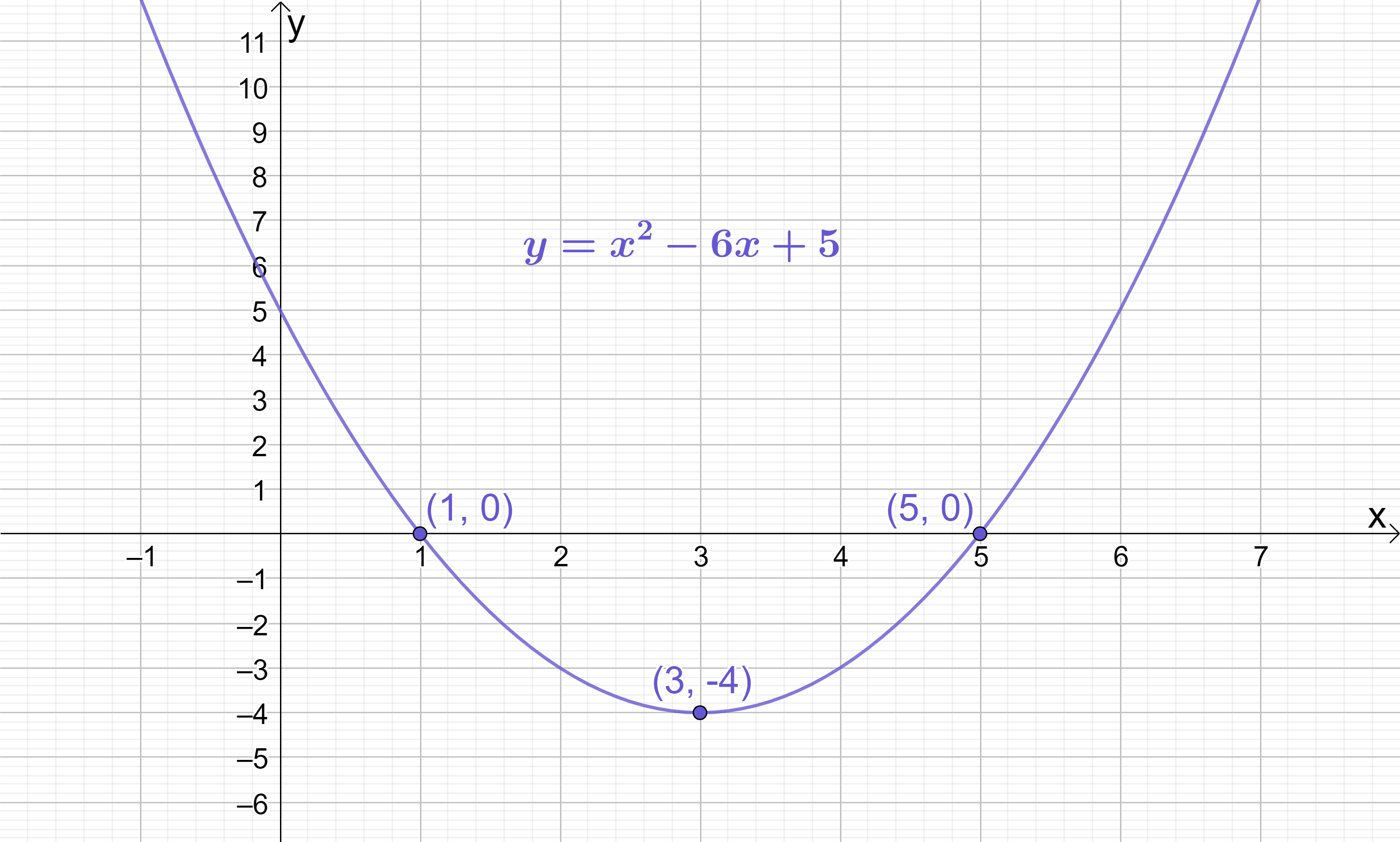
Let’s Complete the Square to find the turning point of y=x^{2}-6x+5. This quadratic’s turning point lies at (3, -4) (so we already know the correct answer we’re working towards).
Before Completing the Square, we need to make sure the a coefficient (the number in front of the x^{2} term) is 1. Since the a coefficient of y=x^{2}-6x+5 is already 1, we don’t have to worry about this in this case.
Let’s now Complete the Square on y=x^{2}-6x+5:
1) Open a bracket and put an \boldsymbol{x} term at the front
\begin{aligned}y&=(x\end{aligned}
2) Add half the \boldsymbol{b} coefficient, then close the bracket and square it
As the b coefficient is -6, half of this is -3:
\begin{aligned}y&=(x-3)^{2}\end{aligned}
3) Separately, multiply out the new bracket and see what constant you have
\begin{aligned}y&=(x-3)^{2} \\[12pt]y&=(x-3)(x-3) \\[12pt]y&=x^{2}-3x-3x+9 \\[12pt]y&=x^{2}-6x+9\end{aligned}
Comparing y=x^{2}-6x+9 to the original quadratic y=x^{2}-6x+5, notice that the first and second terms are the same (both have an x^{2} and a -6x) but the constant at the back (the c coefficient) is off: we have +9 when we should have +5. We fix this in step four:
4) Make an adjustment (add or subtract a number) to ensure the constant ultimately works out the same as the original \boldsymbol{c} coefficient
We have +9 when we should have +5, so we must subtract 4:
\begin{aligned}y&=(x-3)^{2}-4\end{aligned}
Before including the -4, when we expanded the brackets the coefficient worked out as +9. Now, if we expand the brackets again, subtracting 4 will give us the correct c coefficient of +5:
\begin{aligned}y&=(x-3)^{2}-4 \\[12pt]y&=(x-3)(x-3)-4 \\[12pt]y&=x^{2}-3x-3x+9-4 \\[12pt]y&=x^{2}-6x+5\end{aligned}
Expanding y=(x-3)^{2}-4 returns the original quadratic y=x^{2}-6x+5.
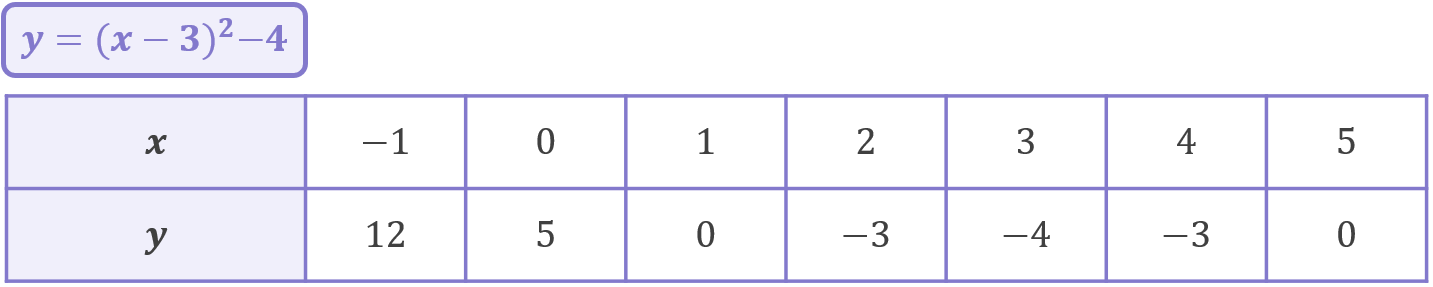
We have now successfully Completed the Square, transforming y=x^{2}-6x+5, which is in the form y=ax^{2}+bx+c, into y=(x-3)^{2}-4, which is in the form y=(x+p)^{2}+q:

5) Once the quadratic is in \boldsymbol{y=(x+p)^{2}+q} form, extract the turning point as \boldsymbol{(-p, q)}
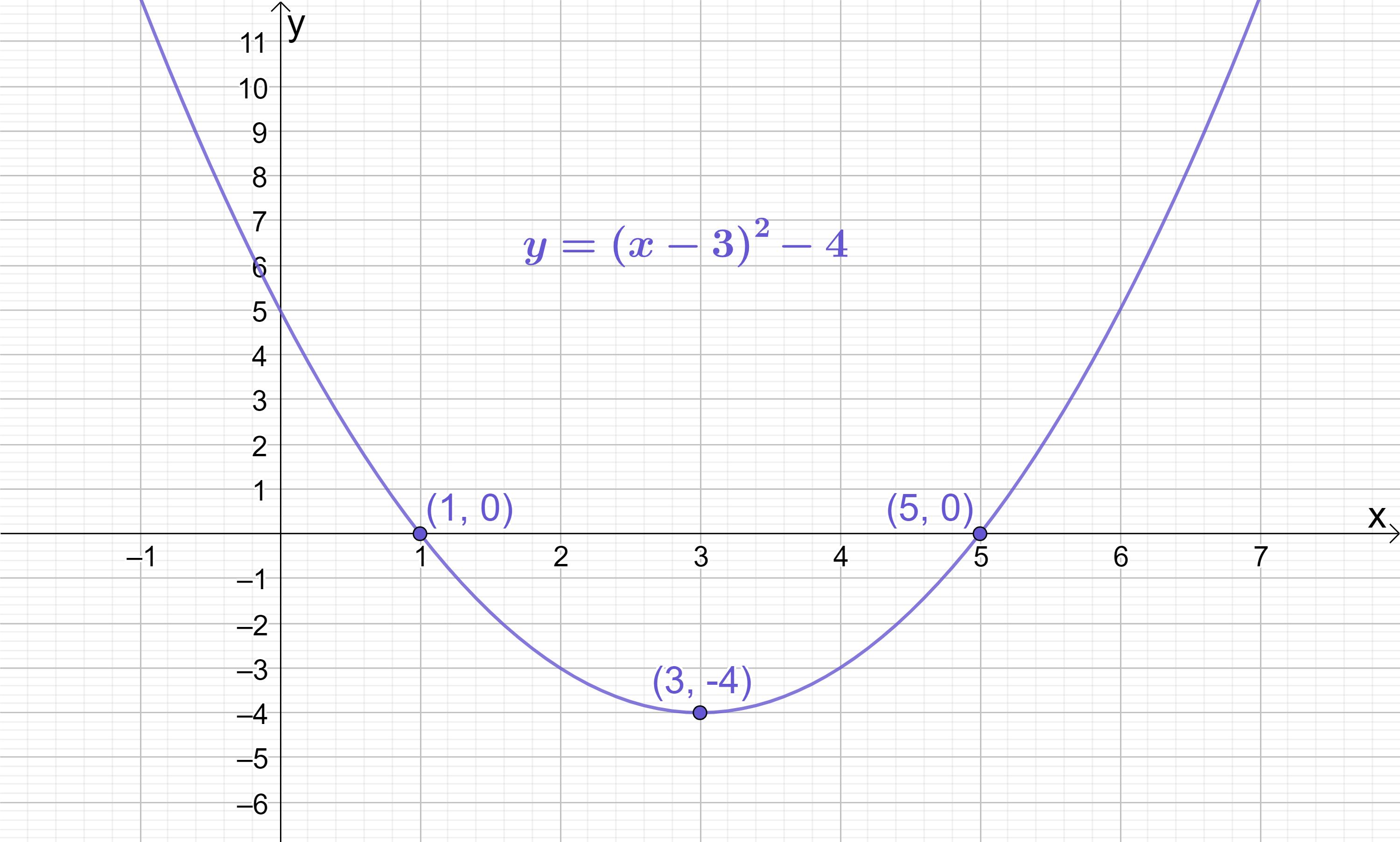
We have successfully transformed y=x^{2}-6x+5 into y=(x-3)^{2}-4. Comparing y=(x-3)^{2}-4 to the general Complete the Square form:
\begin{aligned}y&=(x-3)^{2}-4 \\[12pt]y&=(x+p)^{2}+q\end{aligned}
We can extract that p=-3 and q=-4. Now we can simply state the turning point:
The turning point of a quadratic in y=(x+p)^{2}+q form is (-p, q). Therefore, the turning point of y=(x-3)^{2}-4 is (3, -4). This agrees with the solution I provided at the beginning of this problem.
Let’s be very clear that in the example above all we have done is transform y=x^{2}-6x+5 into y=(x-3)^{2}-4. Basically, we have changed the way the quadratic is written such that it offers us different information, but we have not changed the underlying quadratic itself at all.
This is sort of like having two fractions, let’s say \frac{4}{2} and \frac{6}{3}. Both of these are just equal to 2 aren’t they? So they offer us different information, but the underlying information in each fraction is exactly the same.
Transforming y=x^{2}-6x+5 into y=(x-3)^{2}-4 has not changed the underlying quadratic at all – it has only changed the way it is written. If you populate a coordinate table for each version of the quadratic, you can see that they have exactly the same coordinates, so if you were to graph them, you’d just get the exact same graph twice!
Completing the Square can be a little tricky to get your head around at first, but with practice it really does become easier. Try not to get too caught up in the technique itself; keep it simple and always remember what the whole point of Completing the Square is in the first place:
Completing the Square is a process that transforms a quadratic in the form of the General Equation:
\boldsymbol{y=ax^{2}+bx+c}
Into a quadratic of the form:
\boldsymbol{y=(x+p)^{2}+q}
The benefit of writing a quadratic in the form \boldsymbol{y=(x+p)^{2}+q} is that you can very easily extract the quadratic’s turning point.
The turning point of a quadratic in the form \boldsymbol{y=(x+p)^{2}+q} lies at \boldsymbol{(-p, q)}.
As always, a couple of examples should solidify your understanding of the method.
Complete the Square for the quadratics in the following examples and state their turning point:
Example 1
y=x^{2}+4x+6
Before Completing the Square, we need to make sure the a coefficient (the number in front of the x^{2} term) is 1. Since the a coefficient of y=x^{2}+4x+6 is already 1, we don’t have to worry about this in this case.
Let’s now Complete the Square on y=x^{2}+4x+6:
1) Open a bracket and put an \boldsymbol{x} term at the front
\begin{aligned}y&=(x\end{aligned}
2) Add half the \boldsymbol{b} coefficient, then close the bracket and square it
As the b coefficient is +4, half of this is +2:
\begin{aligned}y&=(x+2)^{2}\end{aligned}
3) Separately, multiply out the new bracket and see what constant you have
\begin{aligned}y&=(x+2)^{2} \\[12pt]y&=(x+2)(x+2) \\[12pt]y&=x^{2}+2x+2x+4 \\[12pt]y&=x^{2}+4x+4\end{aligned}
Comparing y=x^{2}+4x+4 to the original quadratic y=x^{2}+4x+6, notice that the first and second terms are the same but the constant at the back (the c coefficient) is off: we have +4 when we should have +6. We fix this in step four:
4) Make an adjustment (add or subtract a number) to ensure the constant ultimately works out the same as the original \boldsymbol{c} coefficient
We have +4 when we should have +6, so we must add 2:
\begin{aligned}y&=(x+2)^{2}+2\end{aligned}
Now if we try expanding the brackets again, adding 2 will give us the correct c coefficient of +6:
\begin{aligned}y&=(x+2)^{2}+2 \\[12pt]y&=(x+2)(x+2)+2 \\[12pt]y&=x^{2}+2x+2x+4+2 \\[12pt]y&=x^{2}+4x+6\end{aligned}
5) Once the quadratic is in \boldsymbol{y=(x+p)^{2}+q} form, extract the turning point as \boldsymbol{(-p, q)}
We have successfully transformed y=x^{2}+4x+6 into y=(x+2)^{2}+2. Comparing y=(x+2)^{2}+2 to the general Complete the Square form:
\begin{aligned}y&=(x+2)^{2}+2 \\[12pt]y&=(x+p)^{2}+q\end{aligned}
We can extract that p=2 and q=2. Therefore, the turning point of y=(x+2)^{2}+2 is (-2, 2).
A sketch of the quadratic confirms this is the correct turning point:
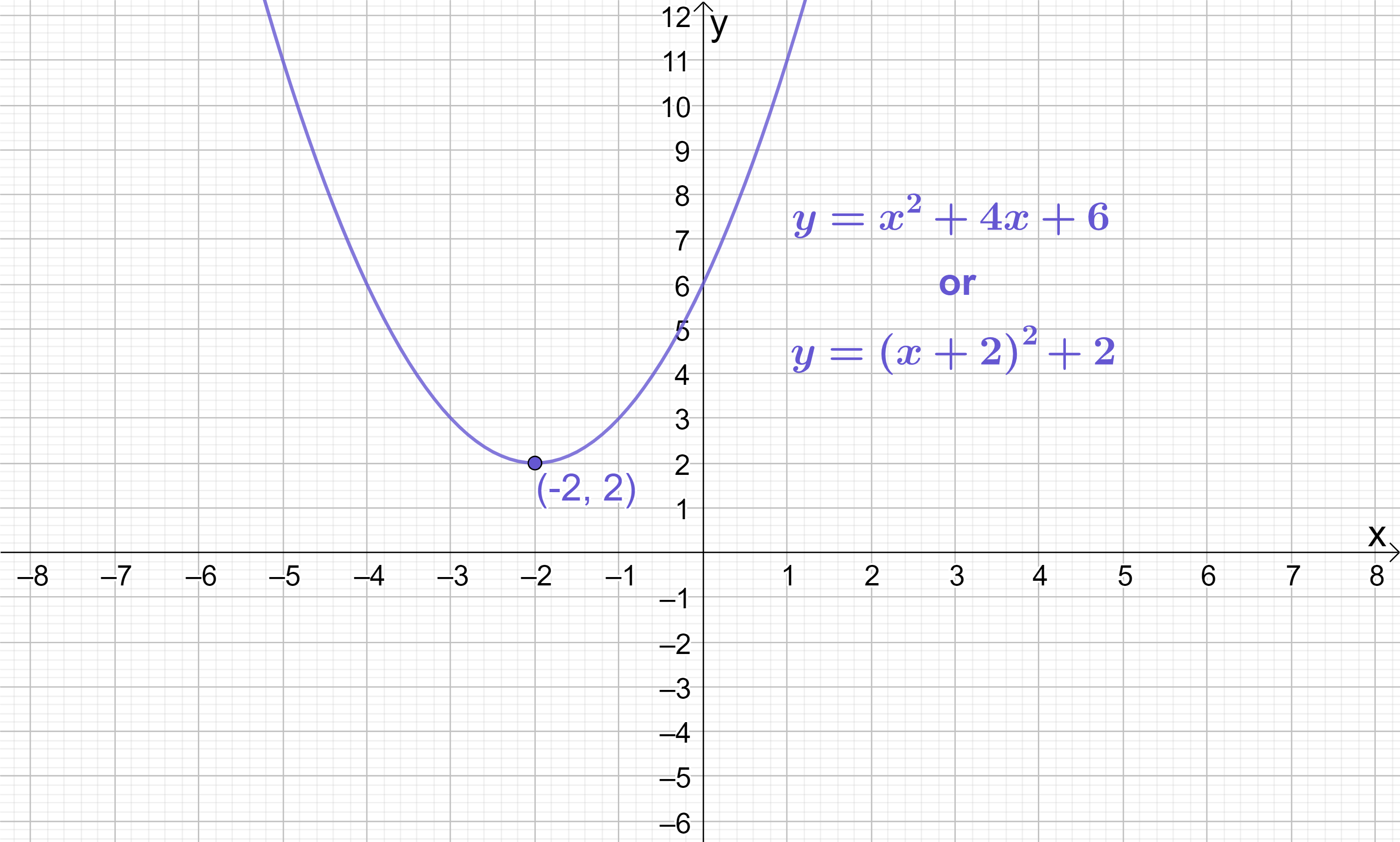
Notice that this quadratic doesn’t have any roots (it never touches the x-axis). For this quadratic, it would have been impossible to use any method for finding the turning point that relies on knowing the roots of the quadratic (since it doesn’t have any!) The only way to find the turning point here is by Completing the Square!
Example 2
y=x^{2}-6x
Before Completing the Square, we need to make sure the a coefficient (the number in front of the x^{2} term) is 1. Since the a coefficient of y=x^{2}-6x is already 1, we don’t have to worry about this in this case.
Let’s now Complete the Square on y=x^{2}-6x:
1) Open a bracket and put an \boldsymbol{x} term at the front
\begin{aligned}y&=(x\end{aligned}
2) Add half the \boldsymbol{b} coefficient, then close the bracket and square it
As the b coefficient is -6, half of this is -3:
\begin{aligned}y&=(x-3)^{2}\end{aligned}
3) Separately, multiply out the new bracket and see what constant you have
\begin{aligned}y&=(x-3)^{2} \\[12pt]y&=(x-3)(x-3) \\[12pt]y&=x^{2}-3x-3x+9 \\[12pt]y&=x^{2}-6x+9\end{aligned}
Comparing y=x^{2}-6x+9 to the original quadratic y=x^{2}-6x, notice that the first and second terms are the same but the constant at the back (the c coefficient) is off: we have +9 when we should have 0. We fix this in step four:
4) Make an adjustment (add or subtract a number) to ensure the constant ultimately works out the same as the original \boldsymbol{c} coefficient
We have +9 when we should have 0 (there is no c coefficient shown in the original quadratic, which means it is 0), so we must subtract 9:
\begin{aligned}y&=(x-3)^{2}-9\end{aligned}
Now if we try expanding the brackets again, subtracting 9 will give us the correct c coefficient of 0:
\begin{aligned}y&=(x-3)^{2}-9 \\[12pt]y&=(x-3)(x-3)-9 \\[12pt]y&=x^{2}-3x-3x+9-9 \\[12pt]y&=x^{2}-6x\end{aligned}
5) Once the quadratic is in \boldsymbol{y=(x+p)^{2}+q} form, extract the turning point as \boldsymbol{(-p, q)}
We have successfully transformed y=x^{2}-6x into y=(x-3)^{2}-9. Comparing y=(x-3)^{2}-9 to the general Complete the Square form:
\begin{aligned}y&=(x-3)^{2}-9 \\[12pt]y&=(x+p)^{2}+q\end{aligned}
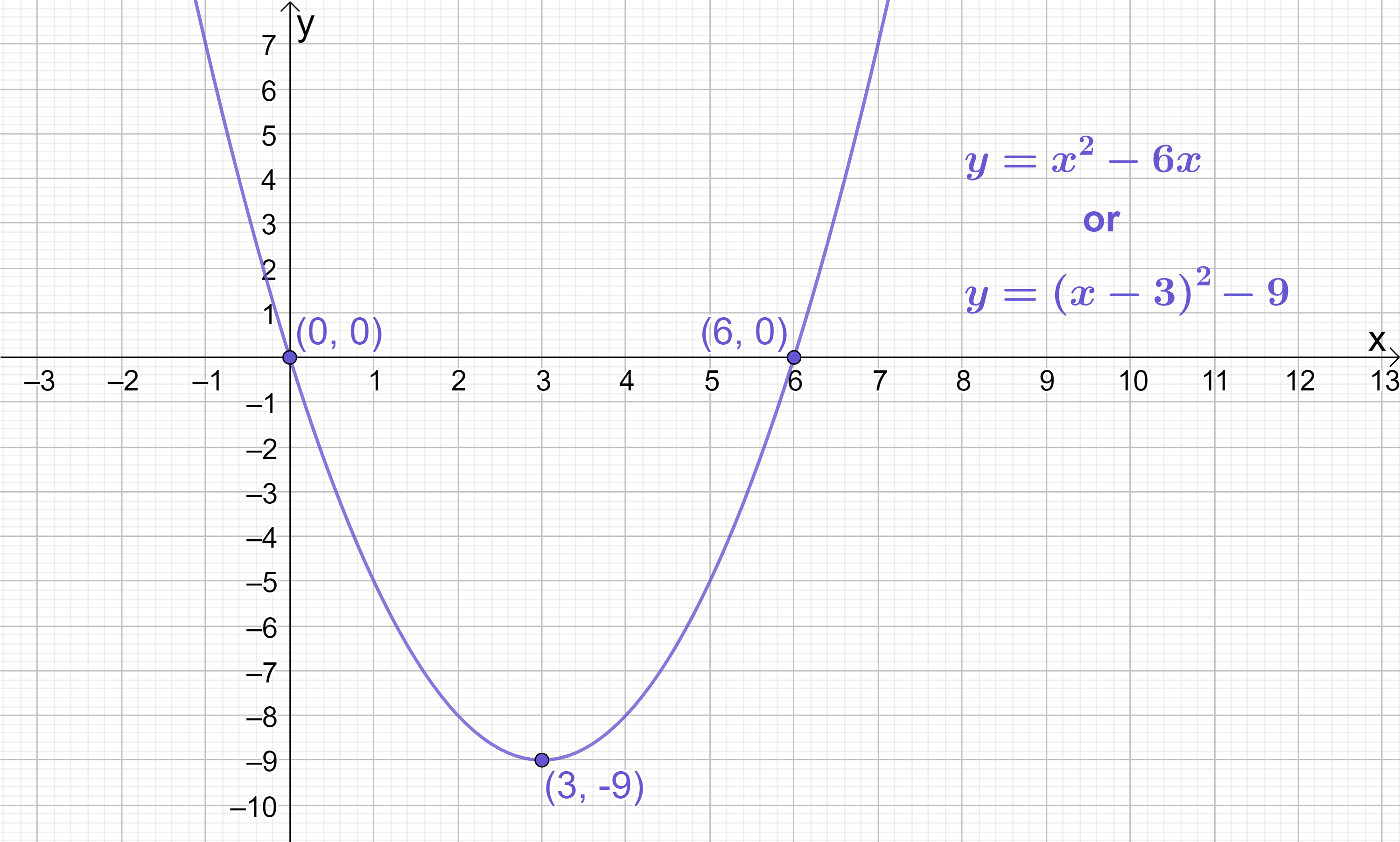
We can extract that p=-3 and q=-9. Therefore, the turning point of y=(x-3)^{2}-9 is (3, -9).
A sketch of the quadratic confirms this is the correct turning point:
Example 3
y=2x^{2}+8x+6
Before Completing the Square, we need to make sure the a coefficient (the number in front of the x^{2} term) is 1. For the first time, we have an a coefficient that is not equal to 1 (here a=2). Completing the Square will be much easier if we first factor out the common factor of 2 from all the x terms as this will bring us back to having an a coefficient of 1:
\begin{aligned}y&=2x^{2}+8x+6 \\[12pt]y&=2(x^{2}+4x)+6\end{aligned}
Let’s be very clear that this first step is not part of the Completing the Square process. This first step is just about getting the quadratic “ready” by arranging it into a friendlier format so we can then go on to Complete the Square more easily. Also notice that we have not factored the 2 out of the c coefficient (+6 in this case) – from experience, the process is simpler if we only take out a common factor from the x terms.
With an a coefficient of 1, we are now ready to now Complete the Square. We mustn’t forget about the 2 that we have factored out – it is important and we can’t just get rid of it (as that would completely alter the quadratic!), so we must carry this factor of 2 throughout our working.
Let’s now Complete the Square on y=2(x^{2}+4x)+6:
1) Open a bracket and put an \boldsymbol{x} term at the front
\begin{aligned}y&=2(x\end{aligned}
2) Add half the \boldsymbol{b} coefficient, then close the bracket and square it
As the b coefficient is +4, half of this is +2:
\begin{aligned}y&=2(x+2)^{2}\end{aligned}
3) Separately, multiply out the new bracket and see what constant you have
\begin{aligned}y&=2(x+2)^{2} \\[12pt]y&=2(x+2)(x+2) \\[12pt]y&=2(x^{2}+2x+2x+4) \\[12pt]y&=2(x^{2}+4x+4) \\[12pt]y&=2x^{2}+8x+8\end{aligned}
Comparing y=2x^{2}+8x+8 to the original quadratic y=2x^{2}+8x+6, notice that the first and second terms are the same but the constant at the back (the c coefficient) is off: we have +8 when we should have +6. We fix this in step four:
4) Make an adjustment (add or subtract a number) to ensure the constant ultimately works out the same as the original \boldsymbol{c} coefficient
We have +8 when we should have +6, so we must subtract 2:
\begin{aligned}y&=2(x+2)^{2}-2\end{aligned}
Now if we try expanding the brackets again, subtracting 2 will give us the correct c coefficient of +6:
\begin{aligned}y&=2(x+2)^{2}-2 \\[12pt]y&=2(x+2)(x+2)-2 \\[12pt]y&=2(x^{2}+2x+2x+4)-2 \\[12pt]y&=2(x^{2}+4x+4)-2 \\[12pt]y&=2x^{2}+8x+8-2 \\[12pt]y&=2x^{2}+8x+6\end{aligned}
5) Once the quadratic is in \boldsymbol{y=(x+p)^{2}+q} form, extract the turning point as \boldsymbol{(-p, q)}
We have successfully transformed y=2x^{2}+8x+6 into y=2(x+2)^{2}-2. Comparing y=2(x+2)^{2}-2 to the general Complete the Square form:
\begin{aligned}y&=2(x+2)^{2}-2 \\[12pt]y&=(x+p)^{2}+q\end{aligned}
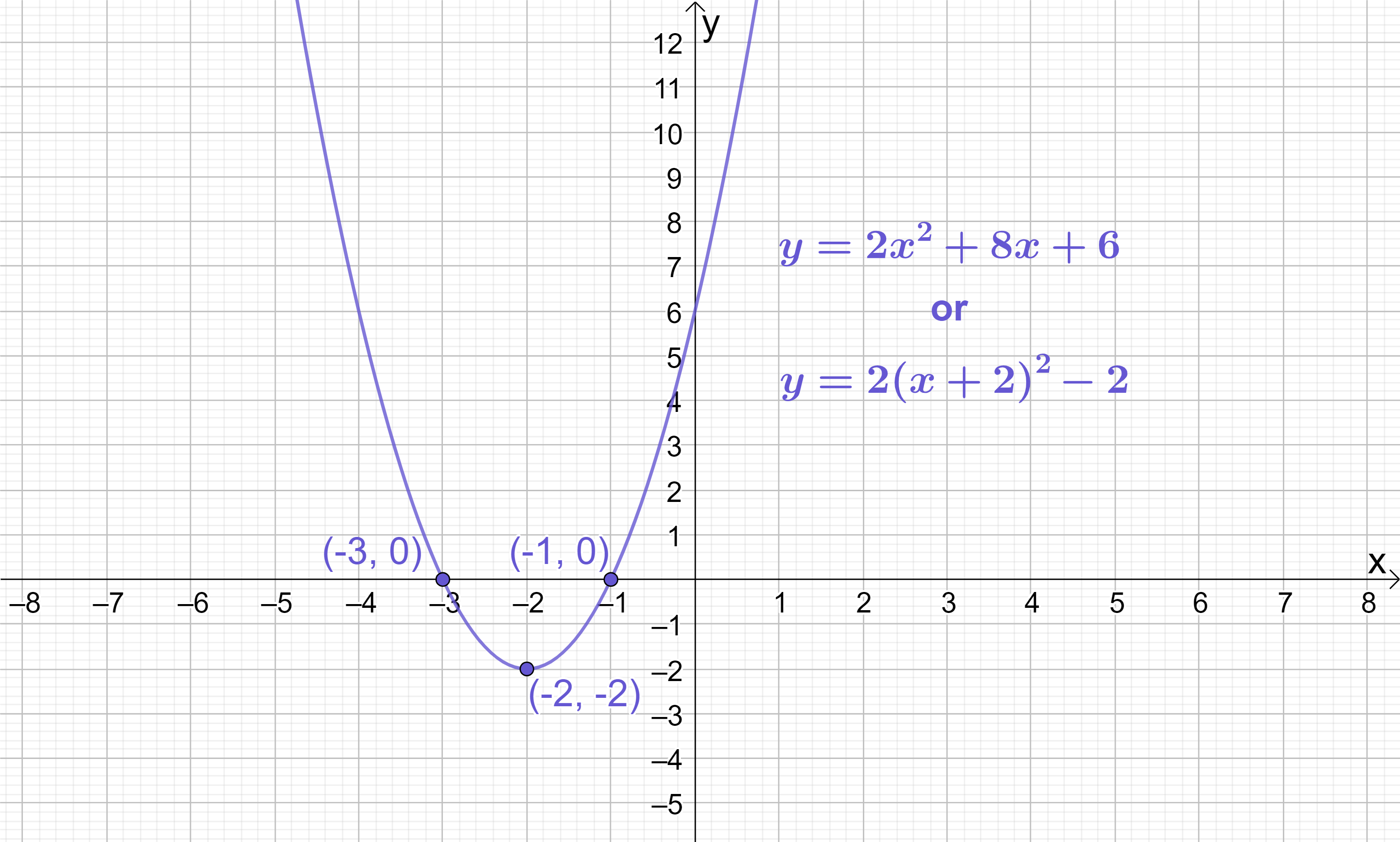
We can extract that p=2 and q=-2. Therefore, the turning point of y=2(x+2)^{2}-2 is (-2, -2).
A sketch of the quadratic confirms this is the correct turning point:
Key Outcomes
Completing the Square is a process which takes a quadratic in standard form y=ax^{2}+bx+c and transforms it into a quadratic of the form y=(x+p)^{2}+q, where the turning point can then easily be extracted as (-p, q).
Before Completing the Square, make sure the a coefficient (the number in front of the x^{2} term) is 1. When you are ready to Complete the Square, the steps are as follows:
1) Open a bracket and put an x term at the front
2) Add half the b coefficient, then close the bracket and square it
3) Separately, multiply out the new bracket and see what constant you have (in most cases, this will not be the same as the constant the quadratic had in its original form, i.e. the c coefficient)
4) Make an adjustment (add or subtract a number) to ensure the constant ultimately works out the same as the original c coefficient
5) Once the quadratic is in y=(x+p)^{2}+q form, extract the turning point as (-p, q)
Completing the Square simply changes the way a quadratic is written such that it offers us different information (i.e. the turning point), but it does not change the underlying quadratic itself at all.
Completing the Square is a more powerful tool for finding the turning point of a quadratic than any method that relies on first knowing the roots because Completing the Square works for all quadratics, including those which do not have roots.






