Circles
Of all the standard 2-D shapes we work with at National 5 level, the circle is the only one with curved edges. This affects the geometry of the shape quite considerably and gives circles some unique characteristics.
It is useful to recall the definitions of various aspects of a circle’s geometry:
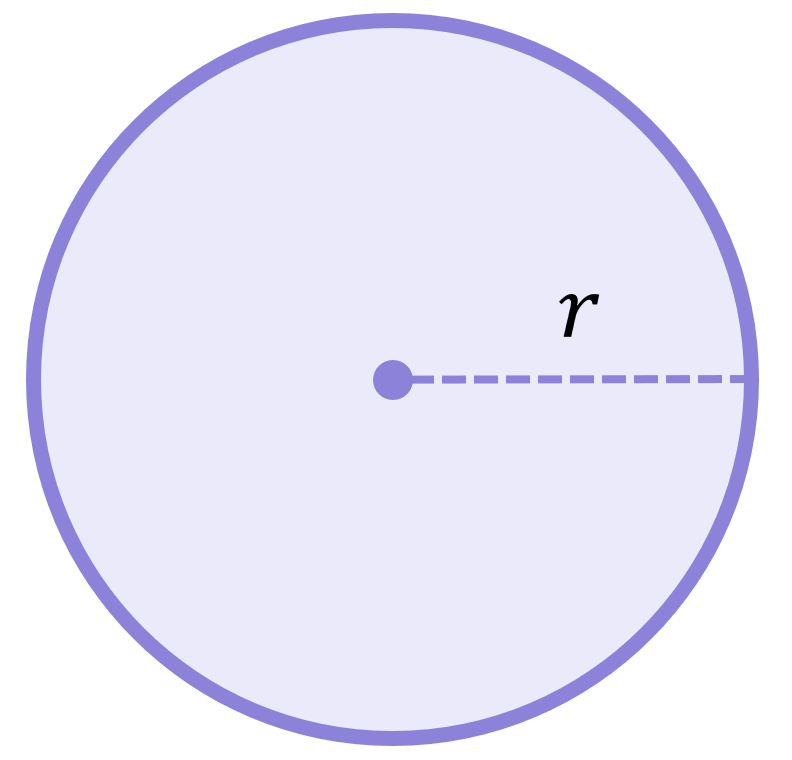
The radius is any straight line going from the centre of a circle to any point on its circumference:
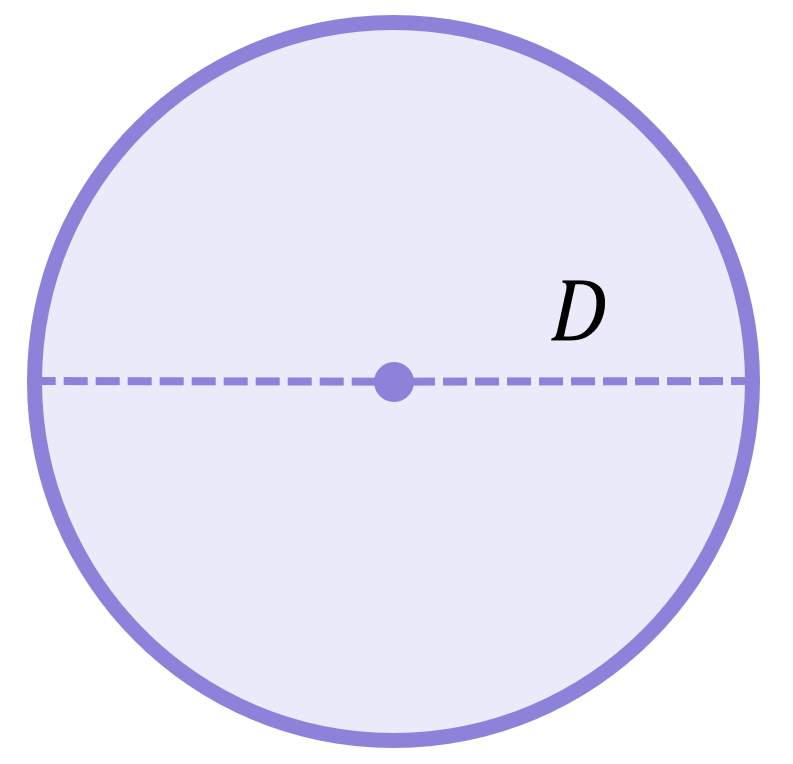
The diameter is any straight line passing through the centre of a circle whose ends both touch the circle’s circumference. A circle’s diameter is always double the length of its radius:
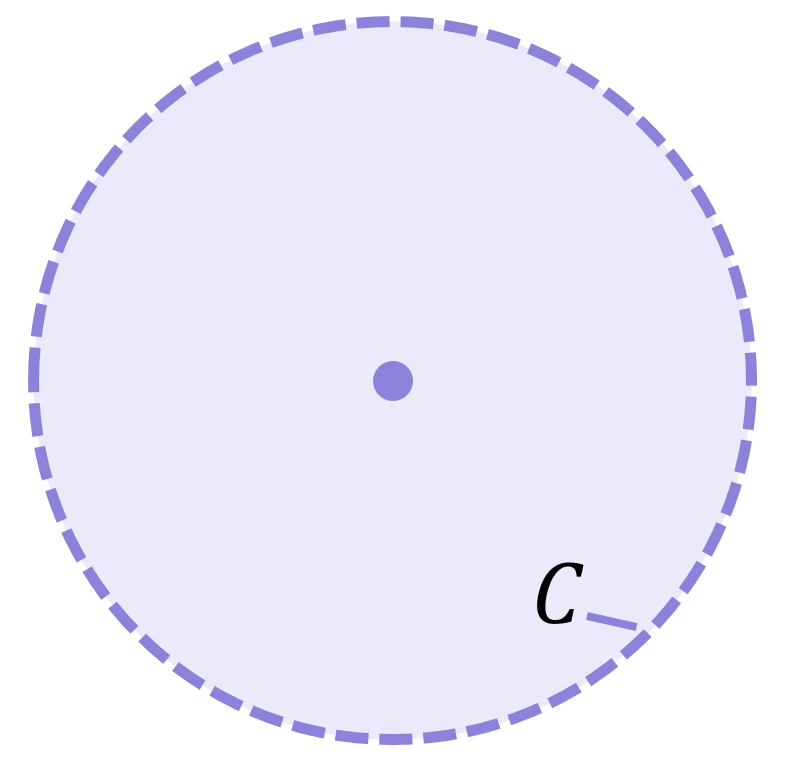
The circumference is the distance around the edge of a circle (in non-curved shapes, this is called the perimeter):
A chord is any line connecting two points on a circle’s circumference that does not pass through the centre of the circle. If the line passed through the centre, it would be a diameter (i.e. the diameter is a special chord):
An arc is any small section of the circumference of a circle:
A sector is the region bounded by two radii and an arc. It is small section of the circle’s overall area. For simplicity, you can think of this as a “pizza slice” shape:
A segment is the region bounded by a chord and an arc:
Expanding on this, there are three laws of circle geometry (pertaining to angles) that you should be aware of.
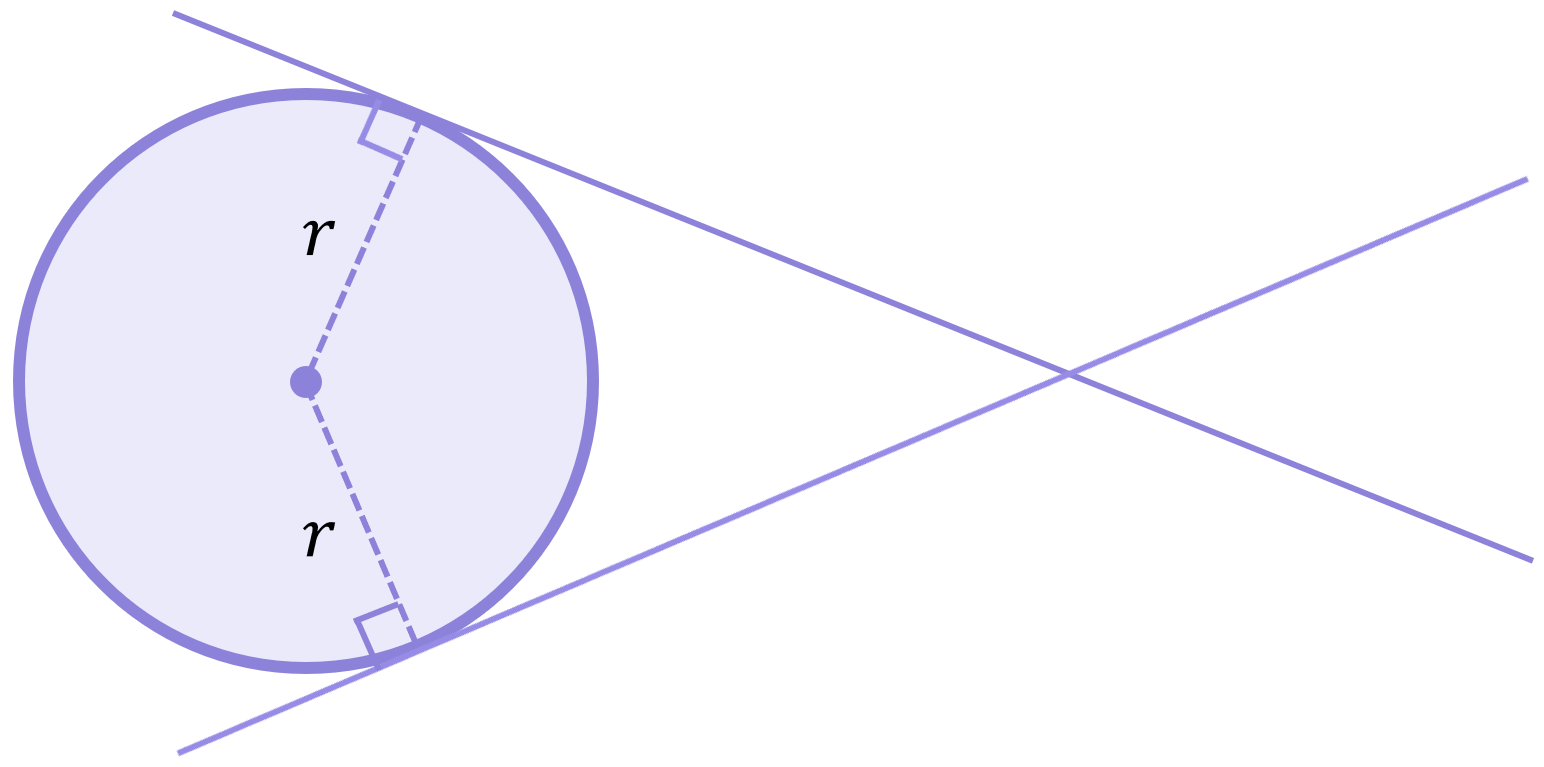
Firstly, a tangent to a curve at a given point is a straight line which “just touches” the curve at that point and no more. In circle geometry, tangents always meet radii at 90^\circ angles:
Secondly, the perpendicular bisector of any chord always passes through the centre of a circle:
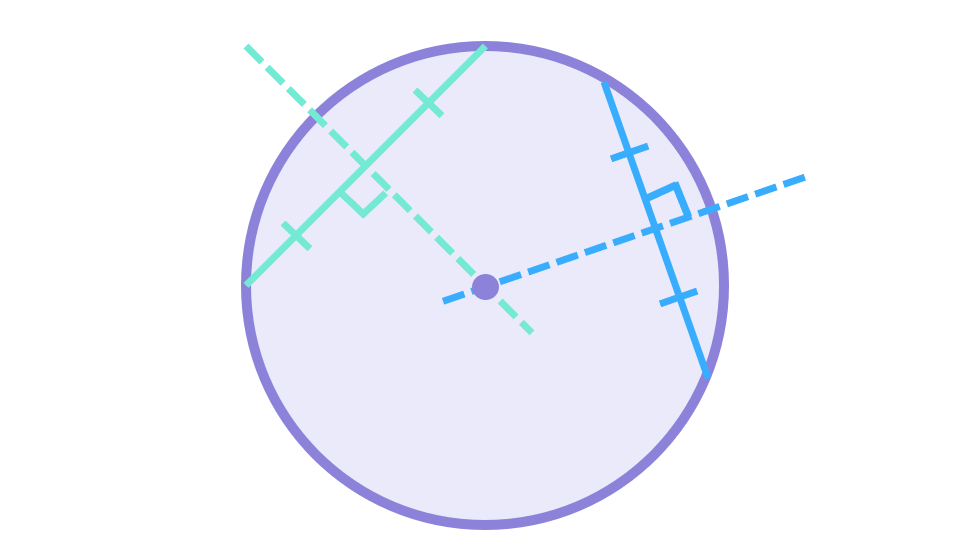
In the diagram above I have shown two possible chords (one in green and one in blue). The perpendicular bisectors of these chords are then shown as dotted lines, and it’s clear that both of these lines pass through the centre of the circle. To be clear, the perpendicular bisector of a chord is the line which passes through the chord at a 90^\circ angle such that it cuts the chord perfectly in half. These are only two of infinitely many possible chords and perpendicular bisectors I could have shown – try drawing a perpendicular bisector of a chord for yourself and you will see that it passes through the centre of the circle.
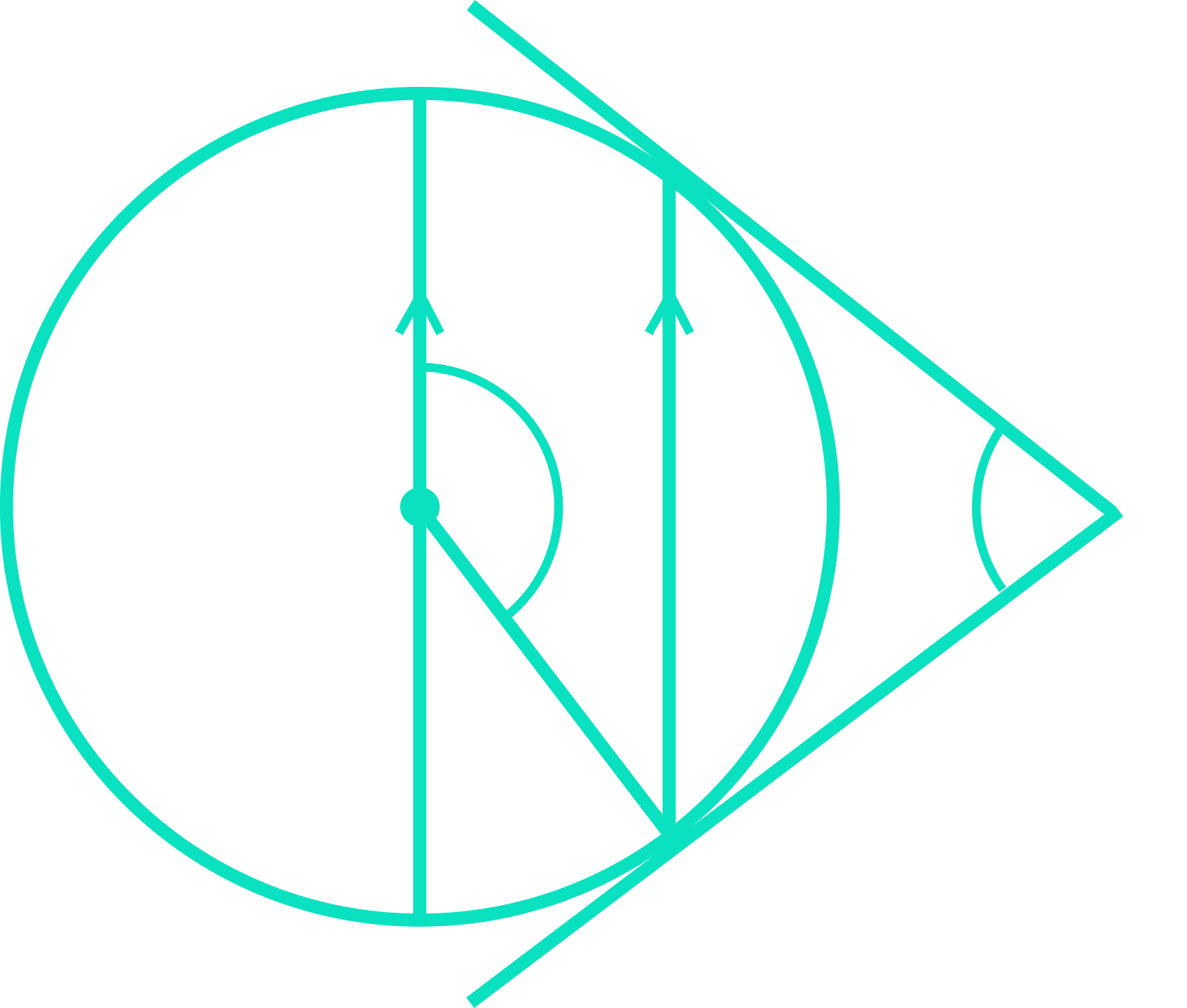
Finally, any two chords that start at opposite ends of a circle’s diameter will always meet at a 90^\circ angle:
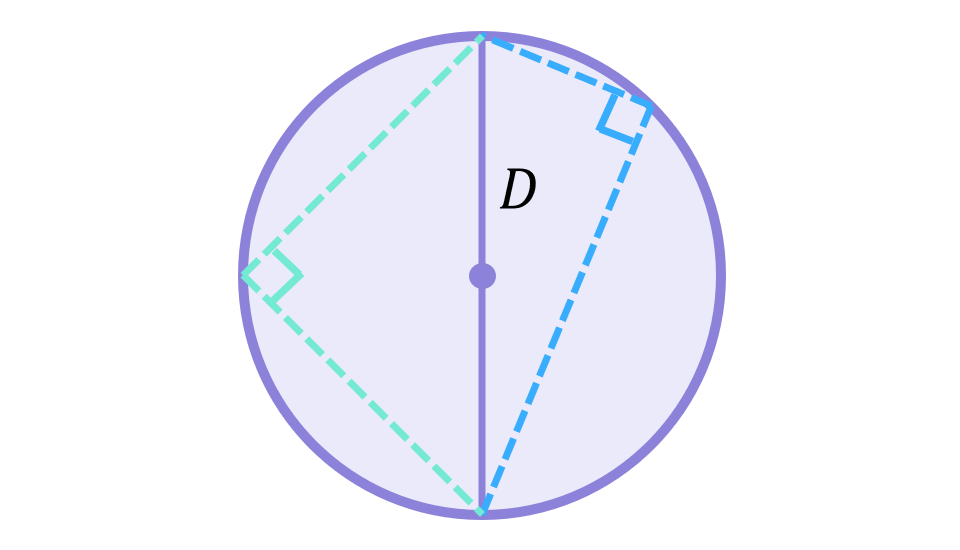
In the diagram above I have shown two possible pairs of chords that start at opposite ends of the diameter (one pair in green and the other in blue), and it is clear they meet at a 90^\circ angle. These are only two of infinitely many possible combinations of chords I could have shown – try drawing two for yourself and you’ll see they always meet at a 90^\circ angle.
In the sections below we examine some of the most common areas of circle knowledge that are regularly challenged in exam questions:
Length of an Arc
Remember that an arc is just a small section of a circle’s circumference. At the ends of any arc, radii can be drawn to create a sector:
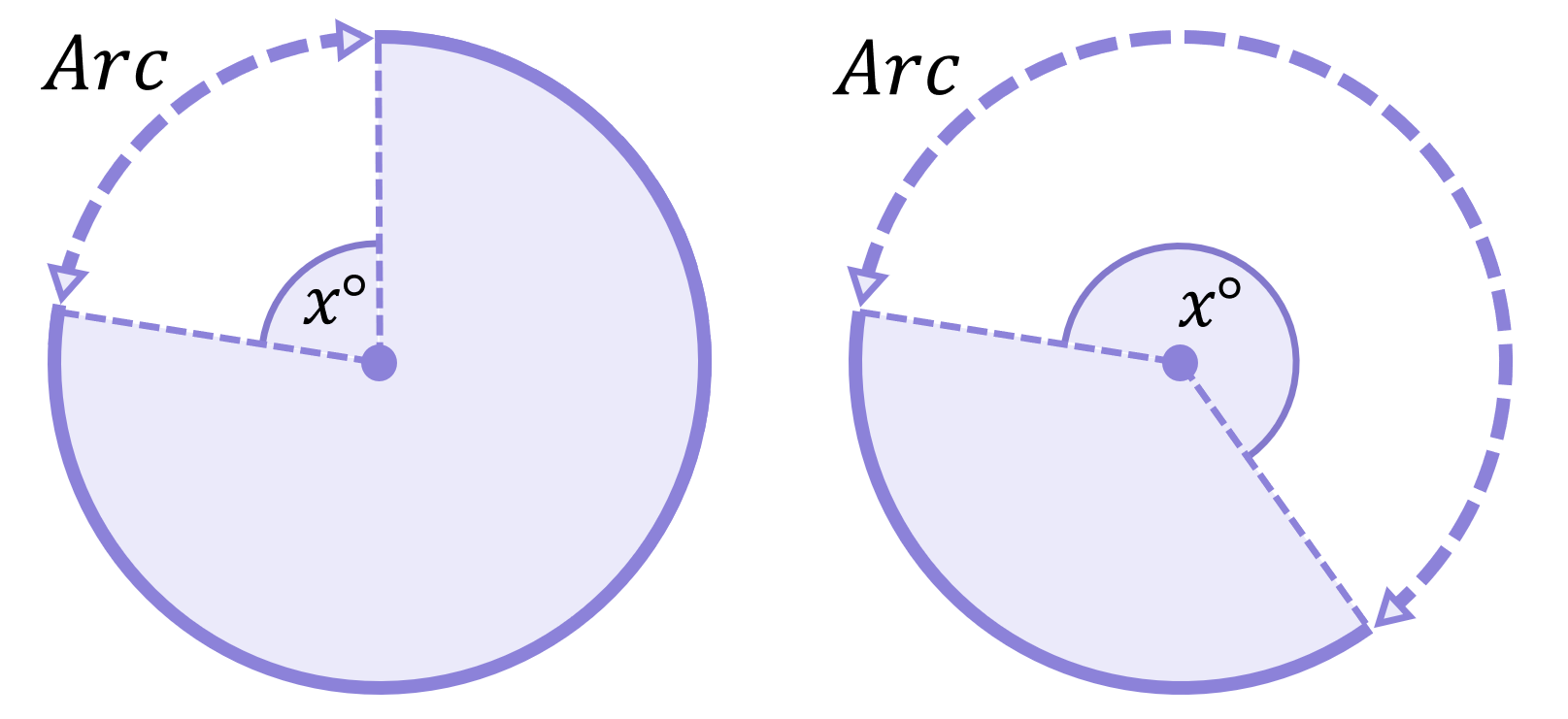
Can you see the angles highlighted in the diagrams above? We say these angles are “subtended” by the arcs.
The length of an arc is determined by the angle subtended by the arc (\boldsymbol{x^\circ}):
\begin{aligned}\textbf{Arc length}=\boldsymbol{\frac{x}{360}\times\pi D}\end{aligned}
In simple terms, this formula works out the “small section” or fraction (\frac{x}{360}) of the overall circumference (\pi D) that the arc length represents. The overall circle, like all circles, has an angle of 360^\circ, so the angle subtended by the arc must be less than this. This fraction (\frac{x}{360}) is then multiplied by the \pi D term which we know is just the circumference of the circle (since C=\pi D), resulting in an answer which is a fraction of the circumference. This should make sense since we defined an arc to be just a small section of the circumference!
Using this formula should not be too challenging, as the following examples show:
Example 1
Calculate the length of the arc shown:
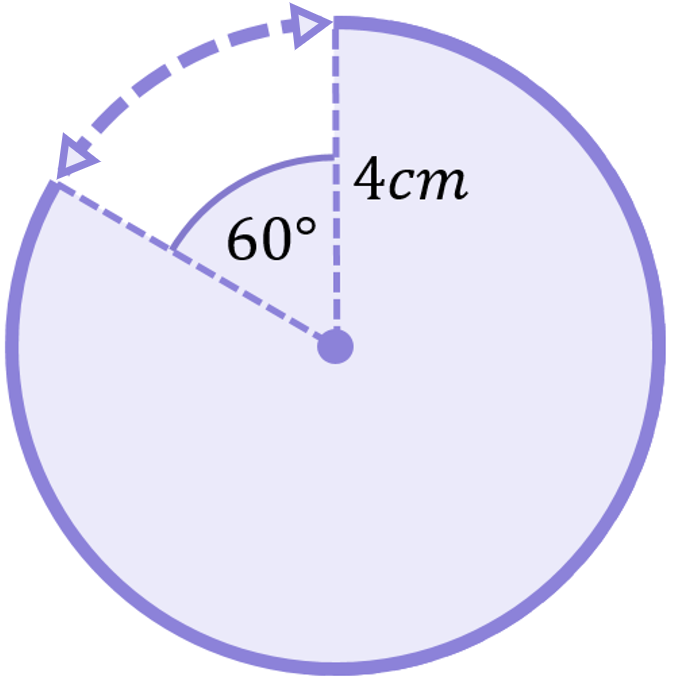
We are given the radius (r=4), from which we can easily calculate the diameter:
\begin{aligned}D&=2r \\[12pt]D&=2(4) \\[12pt]D&=8cm\end{aligned}
Since we are given the angle subtended by the arc, we can employ the new formula we just learned to calculate the length of an arc:
\begin{aligned}\text{Arc length}&=\frac{x}{360}\times\pi D \\[12pt]\text{Arc length}&=\frac{60}{360}\times\pi (8) \\[12pt]\text{Arc length}&=4.2cm\end{aligned}
Example 2
Determine the length of the circle’s diameter:
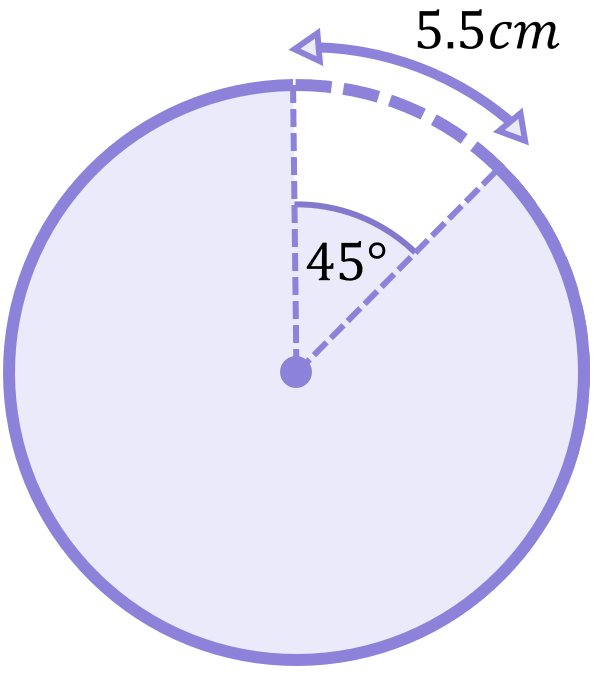
This will require using our new formula in a rearranged form. We must rearrange to make the diameter the subject of the equation:
\begin{aligned}\text{Arc length}&=\frac{x}{360}\times\pi D \\[12pt]360\times\text{Arc length}&=x\times\pi D \\[12pt]\frac{360\times\text{Arc length}}{x}&=\pi D \\[12pt]\frac{360\times\text{Arc length}}{x\pi}&=D \\[12pt]D&=\frac{360\times (5.5)}{(45)\pi} \\[12pt]D&=14cm\end{aligned}
Area of a Sector
Remember that a sector is the “pizza slice” created when an angle is subtended by an arc:
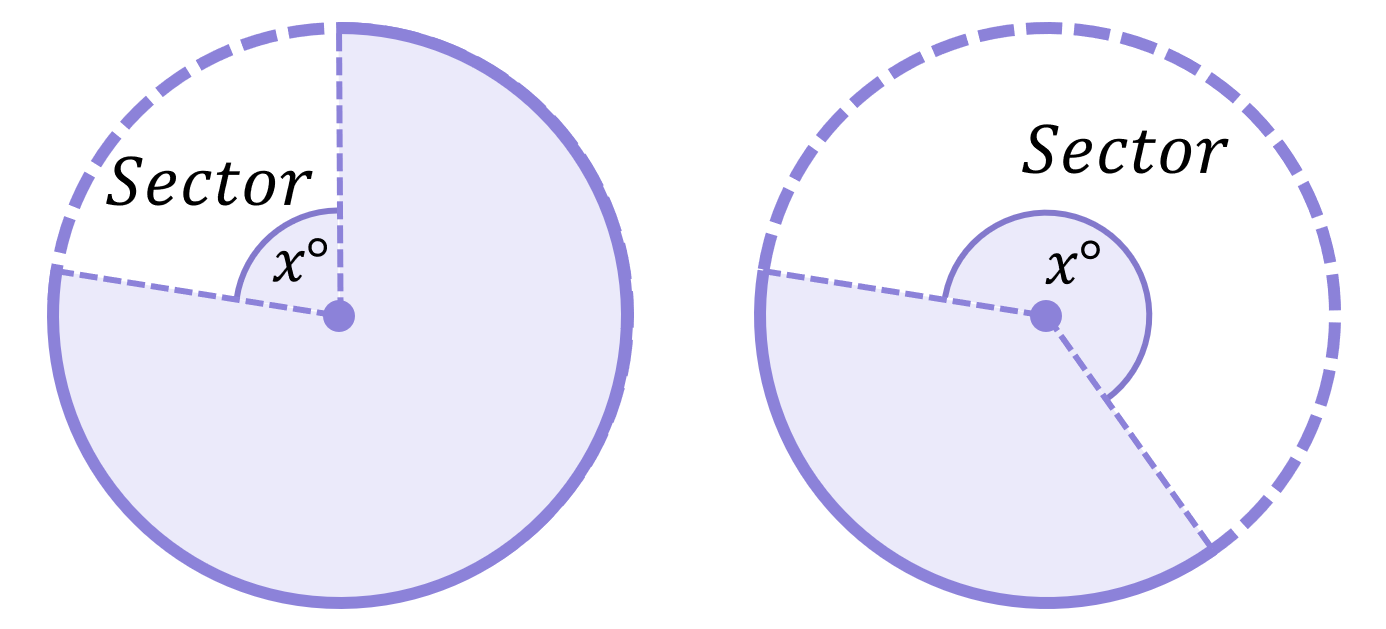
Just like the length of an arc, the area of a sector is also determined by the angle subtended by the arc (\boldsymbol{x^\circ}):
\begin{aligned}\textbf{Sector area}=\boldsymbol{\frac{x}{360}\times\pi r^{2}}\end{aligned}
This formula works in essentially the same way as the previous formula for the length of an arc. In simple terms, this formula works out the “small section” or fraction (\frac{x}{360}) of the overall area (\pi r^{2}) of the circle that the sector represents. The overall circle has an angle of 360^\circ, so the angle subtended by the arc must be less than this. This fraction (\frac{x}{360}) is then multiplied by the \pi r^{2} term which we know is just the area of the full circle (since A=\pi r^{2}), resulting in an answer which is a fraction of the area. This should make sense since we defined a sector to be just a small section of the overall circle’s area!
As with the arc length formula, using the area of a sector formula should not be too challenging, as the following examples show:
Example 3
Calculate the area of the sector shown:
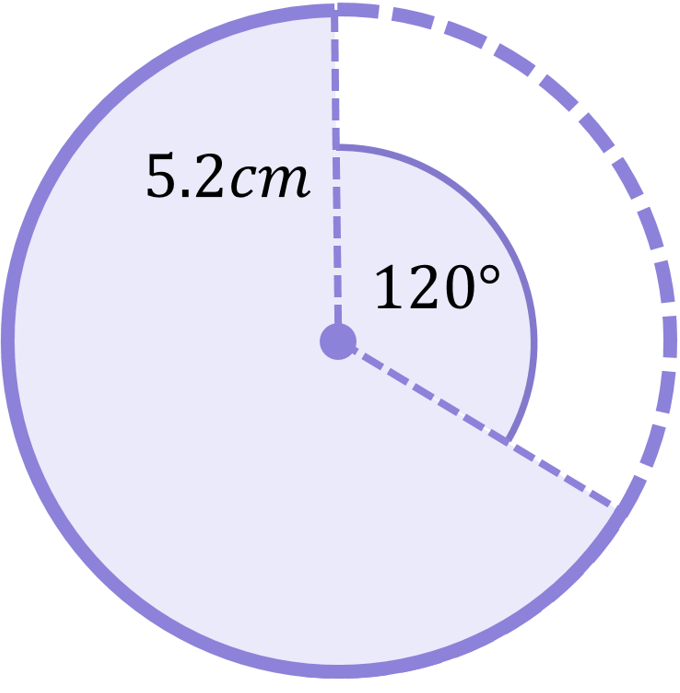
We have all we need to jump right into the sector area calculation:
\begin{aligned}\text{Sector area}&=\frac{x}{360}\times\pi r^{2} \\[12pt]\text{Sector area}&=\frac{120}{360}\times\pi (5.2)^{2} \\[12pt]\text{Sector area}&=28.3cm^{2}\end{aligned}
Example 4
A sector of a circle has an area of 30cm^{2} and an angle of 72^\circ. Calculate the radius of the circle.
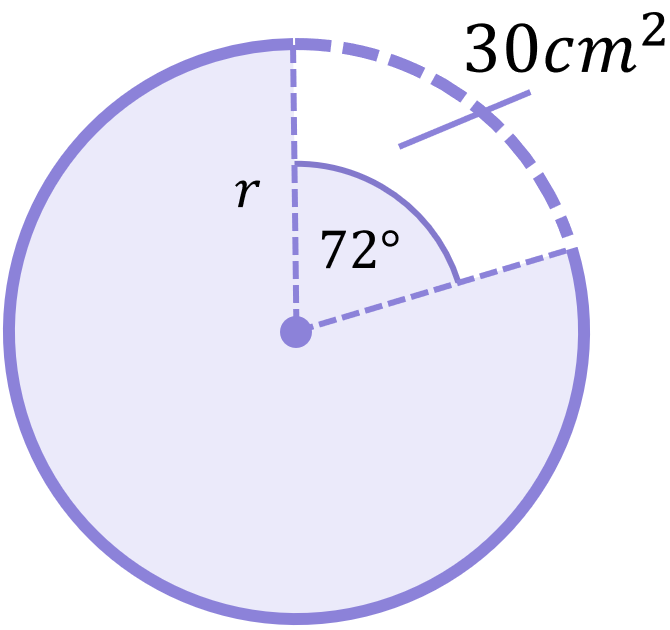
Once again we must rearrange our new formula to make the term we want to calculate (the radius) the subject:
\begin{aligned}\text{Sector area}&=\frac{x}{360}\times\pi r^{2} \\[12pt]360\times\text{Sector area}&=x\times\pi r^{2} \\[12pt]\frac{360\times\text{Sector area}}{x}&=\pi r^{2} \\[12pt]\frac{360\times\text{Sector area}}{x\pi}&=r^{2}\end{aligned}
Substituting what we know into the equation:
\begin{aligned}r^{2}&=\frac{360\times (30)}{(72)\pi} \\[12pt]r^{2}&=47.75 \\[12pt]r&=\sqrt{47.75} \\[12pt]r&=6.9cm\end{aligned}
Related Angles
Example 5
The diagram below shows a circle with centre O:
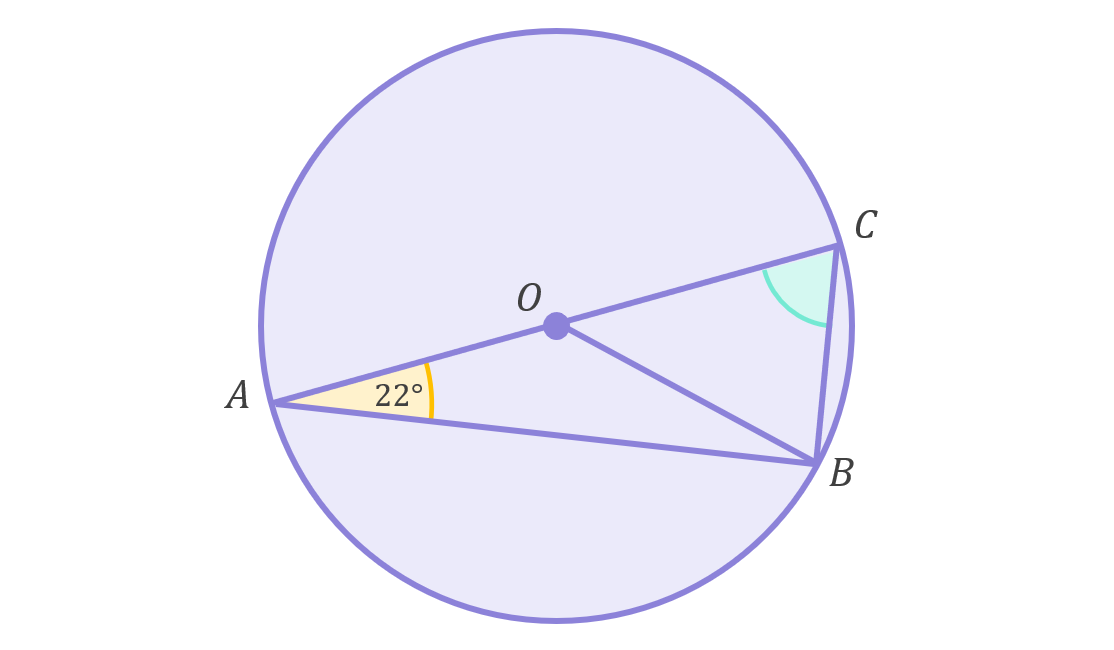
Determine the size of \angle ACB highlighted green in the diagram above.
This example is quite straightforward. AB and BC are chords, and since any two chords that start at opposite ends of a circle’s diameter will always meet at a 90^\circ angle, we know that triangle ABC is right-angled (i.e. \angle ABC=90^\circ):
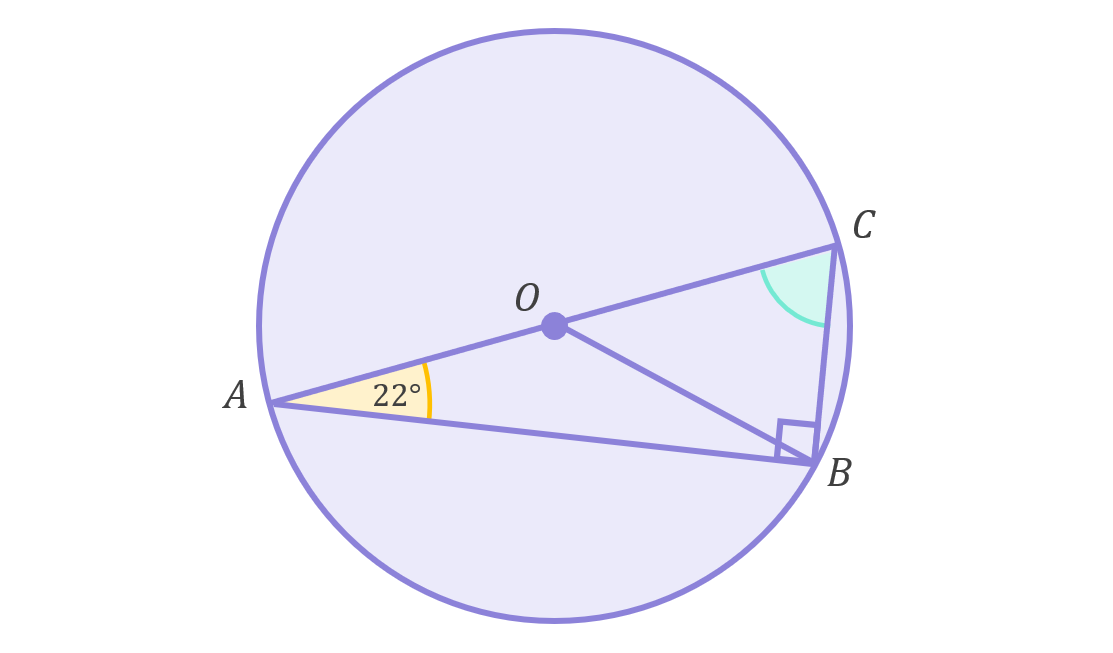
We now know two of the interior angles of triangle ABC – we know that \angle BAC=22^\circ and \angle ABC=90^\circ. Since the interior angles of any triangle always add to 180^\circ, we can calculate \angle ACB as follows:
\begin{aligned}\angle ACB&=180^\circ-\angle ABC-\angle BAC \\[12pt]&=180^\circ-90^\circ-22^\circ \\[12pt]&=68^\circ\end{aligned}
Example 6
The diagram below shows a circle with centre O:
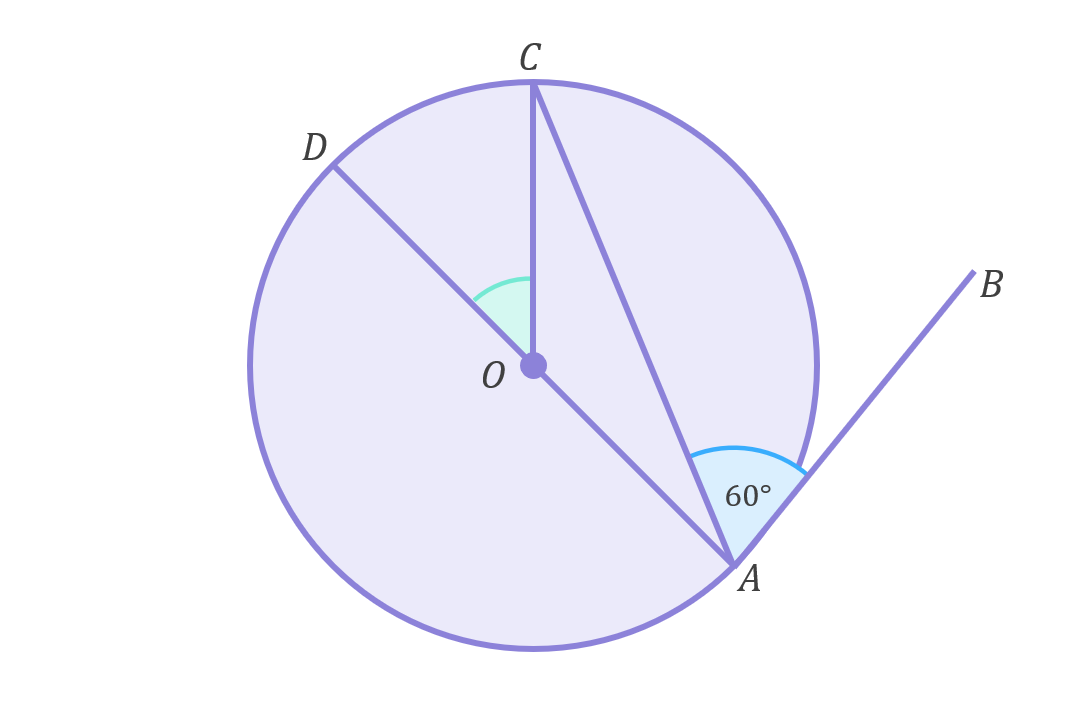
AB is a tangent to the circle.
Given this, determine the size of \angle COD highlighted green in the diagram above.
In circle geometry, tangents always meet radii at 90^\circ angles. Therefore, AB meets AO at a 90^\circ angle, meaning \angle CAO=90^\circ-60^\circ=30^\circ:
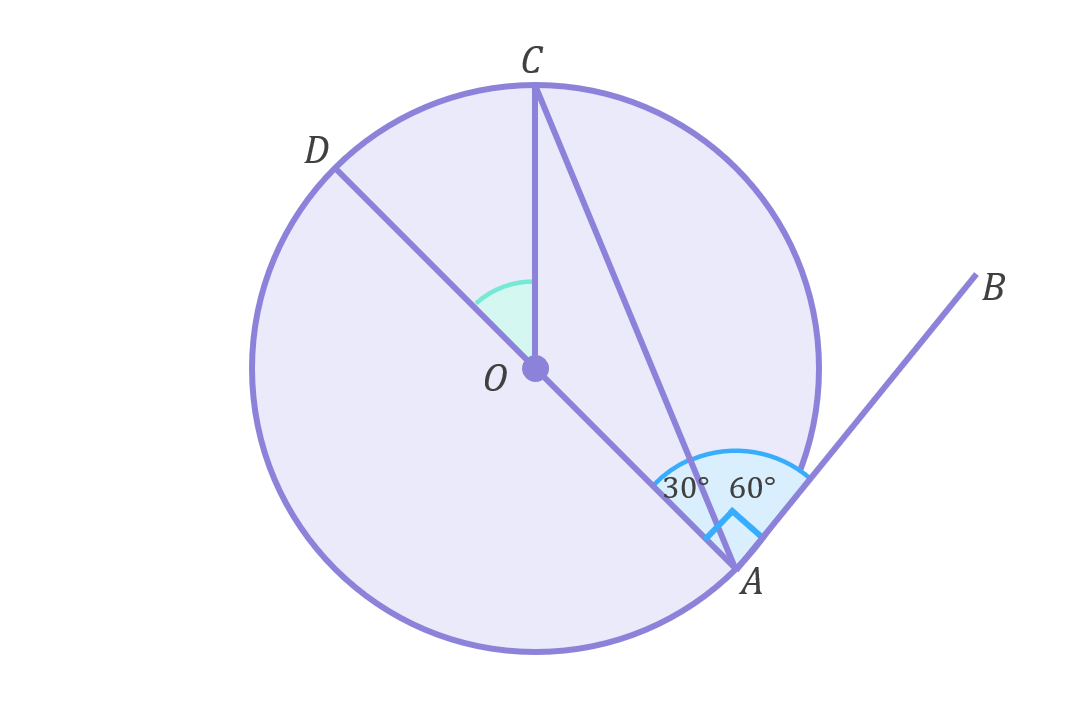
OA and OC are both radii and thus have equal length. Triangle AOC must therefore be isosceles (two equal sides and angles), which means \angle OAC=\angle OCA=30^\circ:
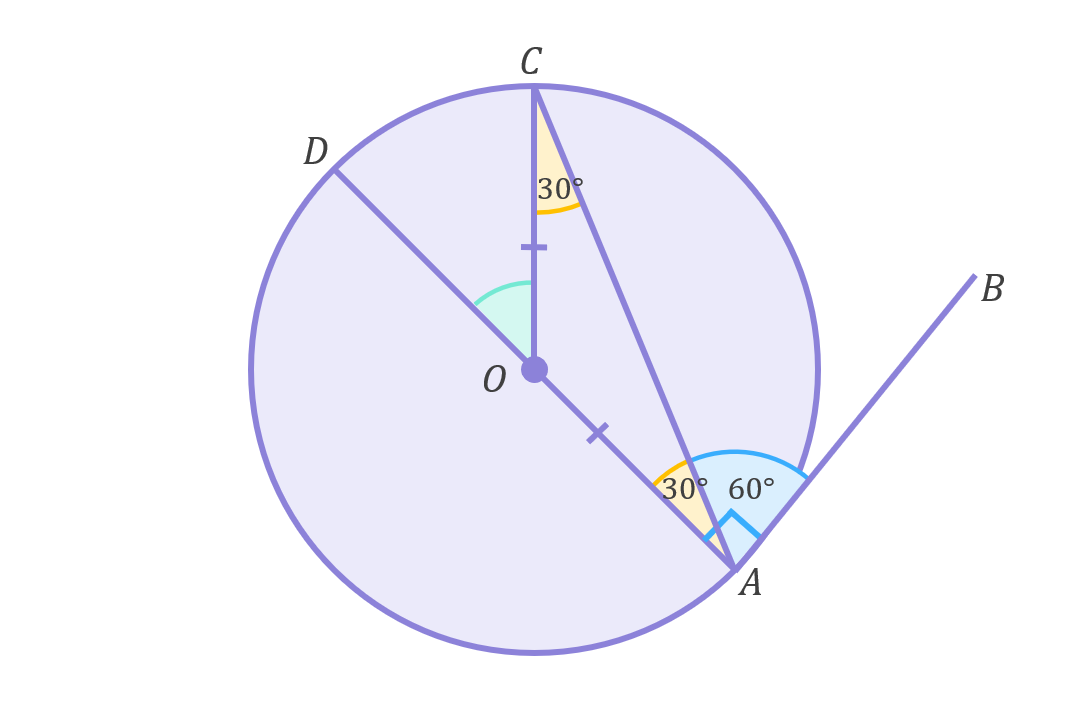
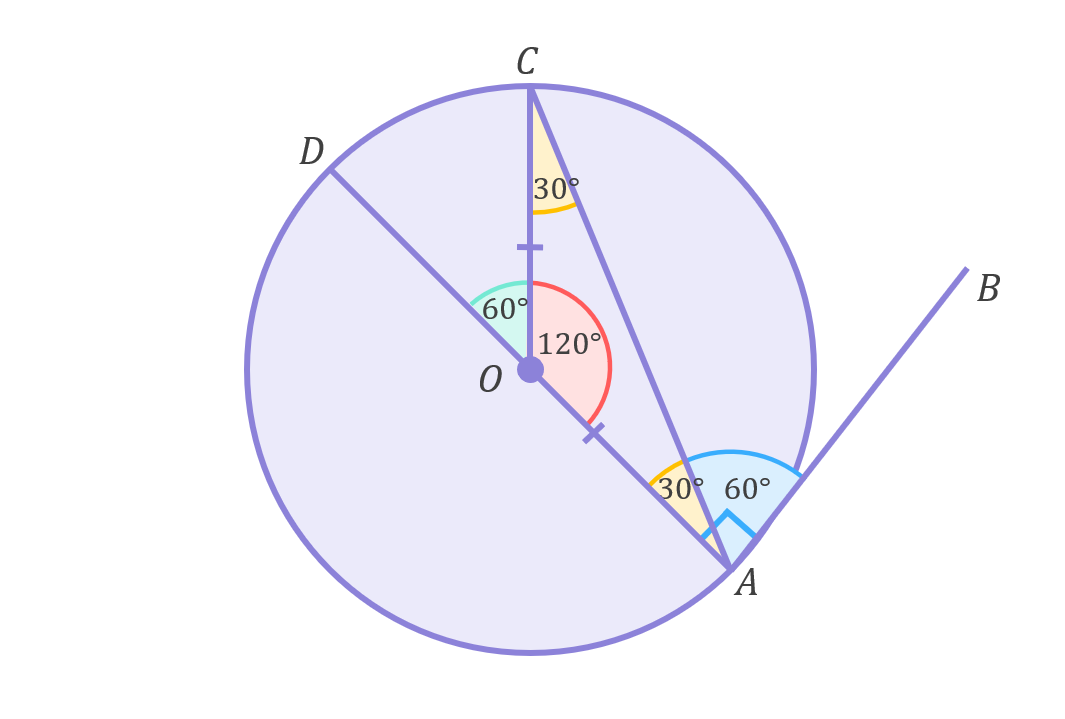
We now know two of the interior angles of triangle AOC – we know that \angle OAC=30^\circ and also that \angle OCA=30^\circ. Since the interior angles of any triangle always add to 180^\circ, we can calculate \angle AOC as follows:
\begin{aligned}\angle AOC&=180^\circ-\angle OAC-\angle OCA \\[12pt]&=180^\circ-30^\circ-30^\circ \\[12pt]&=120^\circ\end{aligned}
And finally, since supplementary angles (i.e. angles that lie along a straight line) always add to 180^\circ, \angle COD (the green angle the question asked us to calculate) can be calculated as follows:
\begin{aligned}\angle COD&=180^\circ-\angle AOC \\[12pt]&=180^\circ-120^\circ \\[12pt]&=60^\circ\end{aligned}
Further Circle Geometry Question Types
Below are two further very standard examples of the types of circle geometry questions you may face in your National 5 exam. These examples rely on your knowledge of Pythagoras’ Theorem (in fact, these examples are copied from the “Converse of Pythagoras” topic from the Trigonometry chapter), but it is worth including them again here for completeness.
Example 7
The diagram below shows the cross-section of a subway tunnel:
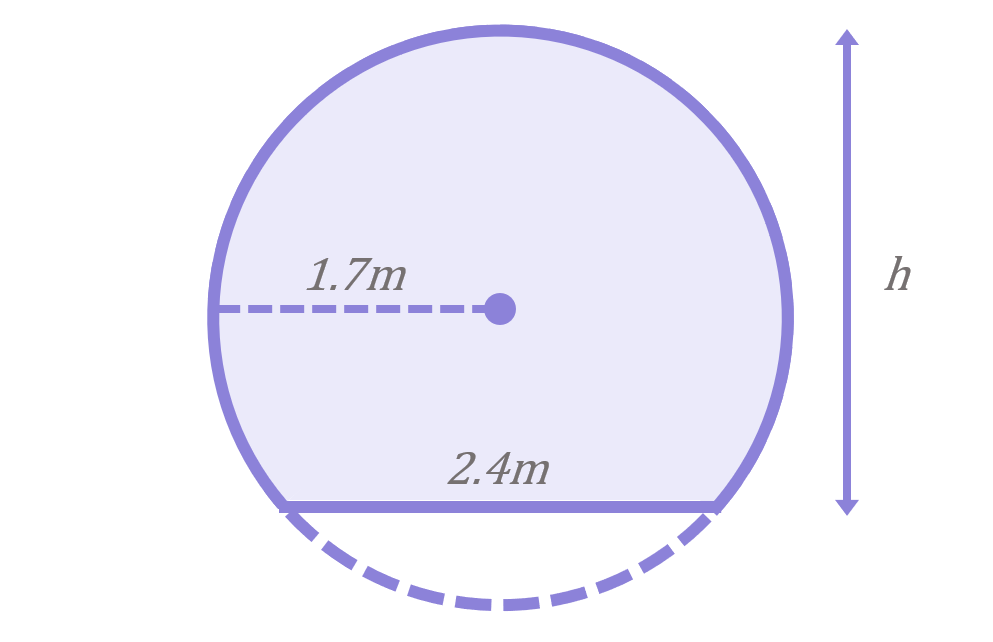
The radius of the tunnel is 1.7m and the width of the floor of the tunnel is 2.4m.
Calculate the height of the tunnel (labelled h in the diagram above).
Although there is no obvious right-angled triangle in this diagram to start with, we can add lines to create one as follows:
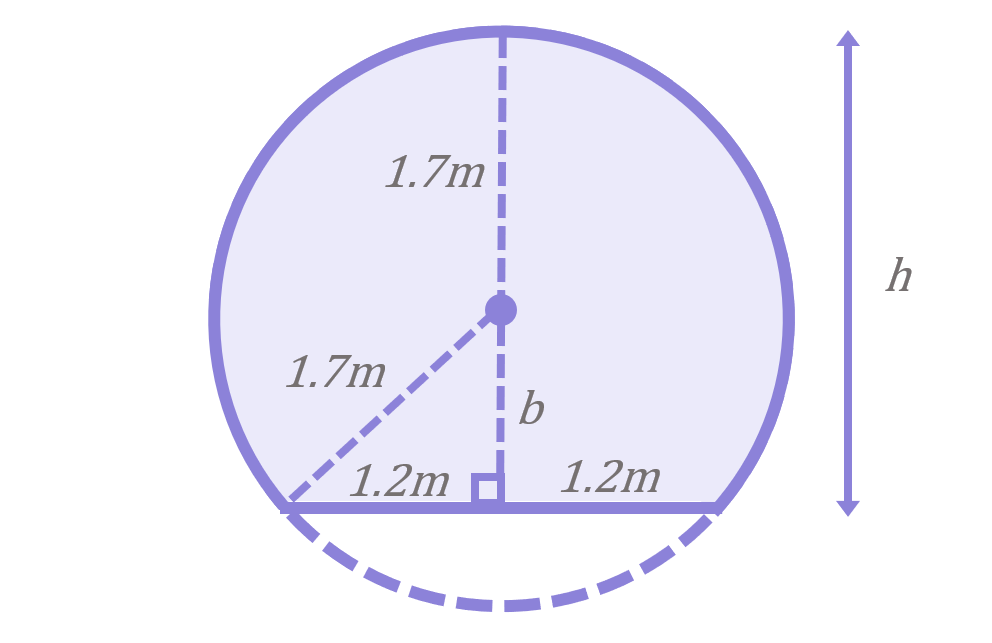
If we add a line (labelled b in the diagram above) running vertically from the centre to the floor of the tunnel, this creates a right-angle and splits the width of the floor in half. We can then draw on a radius connecting the centre to the edge of the floor which creates a right-angled triangle. Since all radii in a circle are the same length, we know this line is 1.7m long. Finally, we can add another radius from the centre to the roof of the tunnel, which again will be 1.7m long. With these new lines in place, it is clear that the height of the tunnel, h, is equal to:
\begin{aligned}h=b+1.7\end{aligned}
We can calculate b using the Converse of Pythagoras:
\begin{aligned}b^{2}&=a^{2}-c^{2} \\[12pt]b^{2}&=(1.7)^{2}-(1.2)^{2} \\[12pt]b^{2}&=1.45 \\[12pt]b&=\sqrt{1.45} \\[12pt]b&=1.2m\end{aligned}
And therefore the height is:
\begin{aligned}h&=b+1.7 \\[12pt]h&=1.2+1.7 \\[12pt]h&=2.9m\end{aligned}
Example 8
The diagram below shows the cross-section of rain gutter with some water in it:
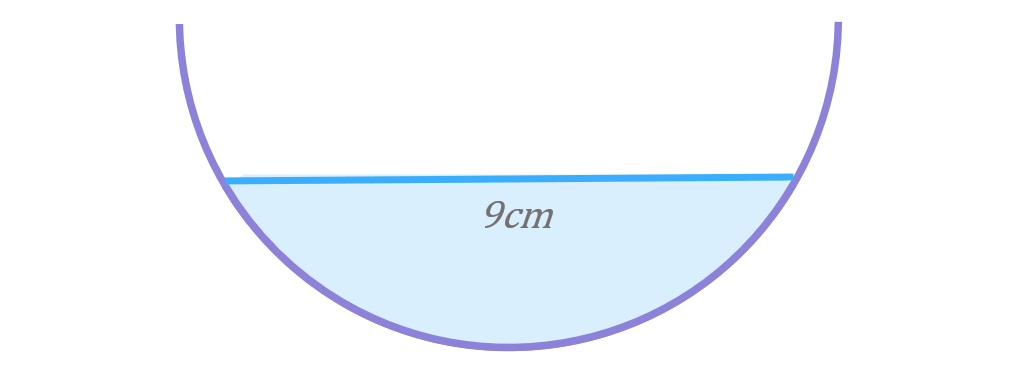
The gutter is a semicircle with radius of 5cm and the width of the surface of the water is 9cm.
Calculate the depth of the water in the gutter.
Again there is no obvious right-angled triangle in this diagram to start with, but as before we can add lines to create one as follows:
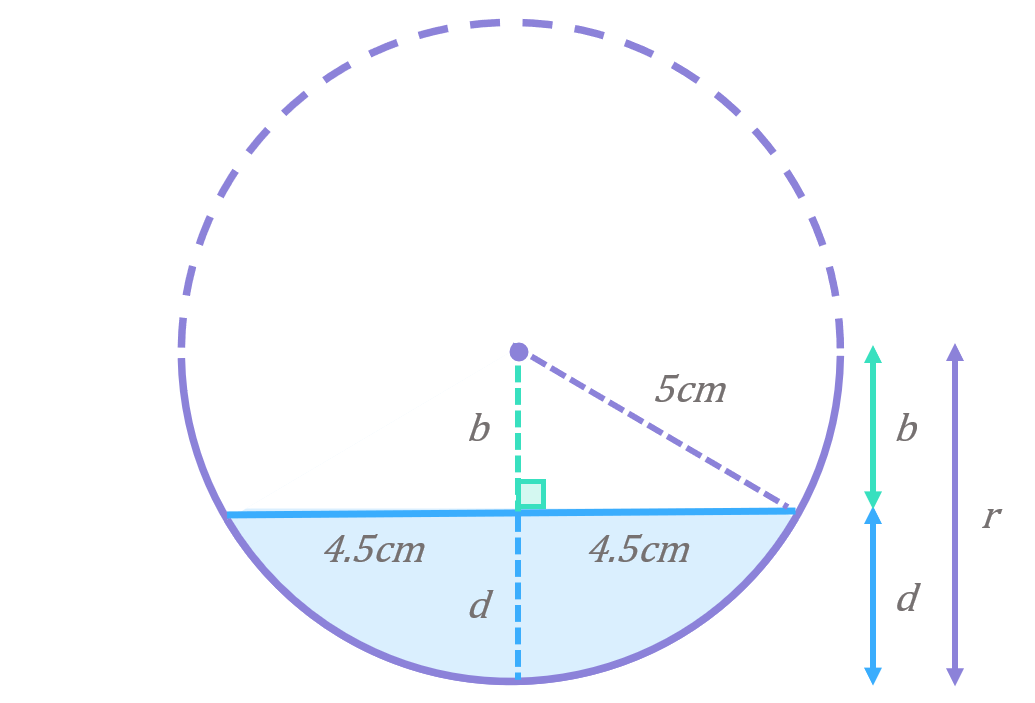
Drawing on two radii – one from the centre to the edge of the water, and one from the centre to the bottom of the gutter – creates a right-angled triangle and splits the surface of the water in half. Since all radii in a circle are the same length, we know both of these lines are 5cm long.
Based on the diagram, it is clear that the depth of the water, labelled d, can be calculated by subtracting the length b from the length of a radius:
\begin{aligned}d=r-b\end{aligned}
Since it represents the length of a radius we know r=5cm, so we just need to calculate b which we can do using the Converse of Pythagoras:
\begin{aligned}b^{2}&=a^{2}-c^{2} \\[12pt]b^{2}&=(5)^{2}-(4.5)^{2} \\[12pt]b^{2}&=4.75 \\[12pt]b&=\sqrt{4.75} \\[12pt]b&=2.2cm\end{aligned}
And therefore the depth of that water, d, is:
\begin{aligned}d&=r-b \\[12pt]d&=5-2.2 \\[12pt]d&=2.8cm\end{aligned}
Key Outcomes
A tangent to a curve at a given point is a straight line which “just touches” the curve at that point and no more. In circle geometry, tangents always meet radii at 90^\circ angles.
The perpendicular bisector of any chord always passes through the centre of a circle. The perpendicular bisector of a chord is the line which passes through the chord at a 90^\circ such that it cuts the chord perfectly in half.
Any two chords that start at opposite ends of a circle’s diameter will always meet at a 90^\circ angle.
Both the length of an arc and the area of a sector are determined by the angle subtended by the arc (x^\circ):
\begin{aligned}\text{Arc length}&=\frac{x}{360}\times\pi D \\[18pt]\text{Sector area}&=\frac{x}{360}\times\pi r^{2} \\[18pt]\end{aligned}