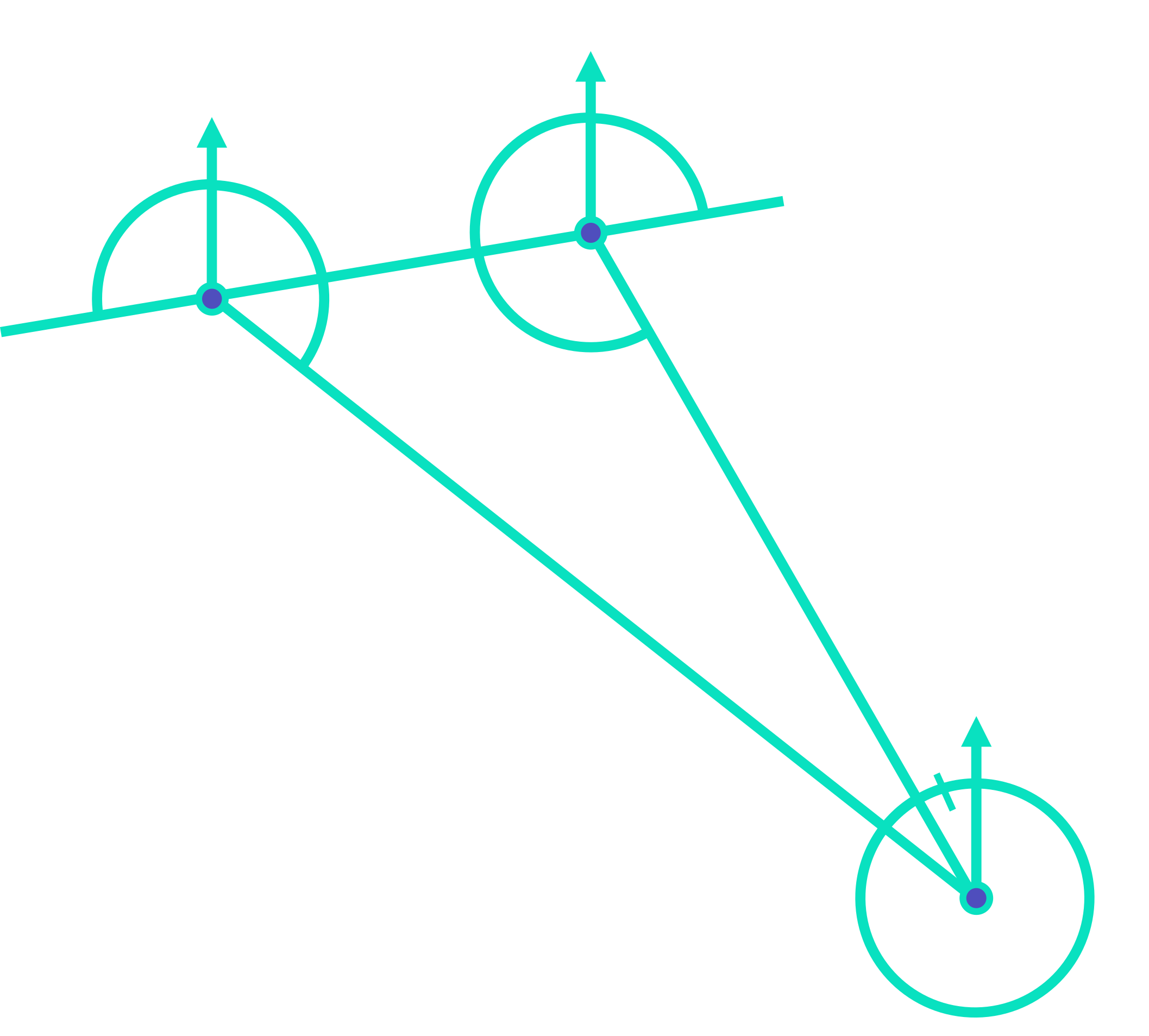
What are Bearings?
Bearings is the major area of application of non-right-angled trigonometry in the National 5 course. When the Sine Rule, Cosine Rule or triangle area formula come up in your exam, there is a very good chance it will be in the context of a bearings question.
Bearings are a method of describing direction which have long been used for navigation, particularly by sailors on old fashioned ships (long before the invention of satellites and GPS).
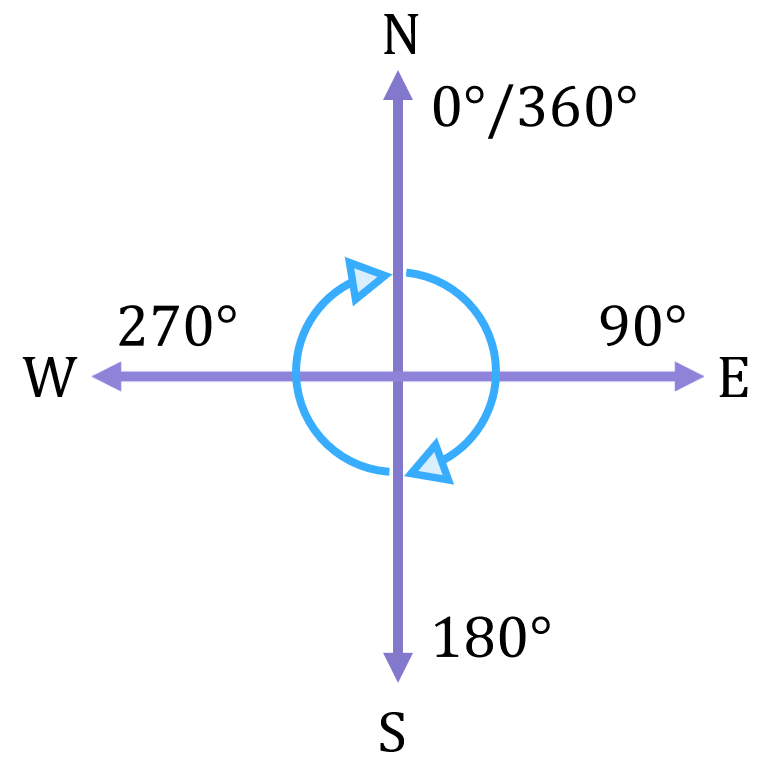
The system of bearings is based on the traditional NESW compass directions:

Moving clockwise from North, you would have to turn 90^\circ to be facing East, and if you turn a further 90^\circ you would be facing South, and so on. By the time you’ve turned a full 360^\circ (i.e. a full circle), you’re back facing North again:
North East lies right in the middle of North and East, South East lies right in the middle of South and East, and so on, so the diagram can be extended as shown below:
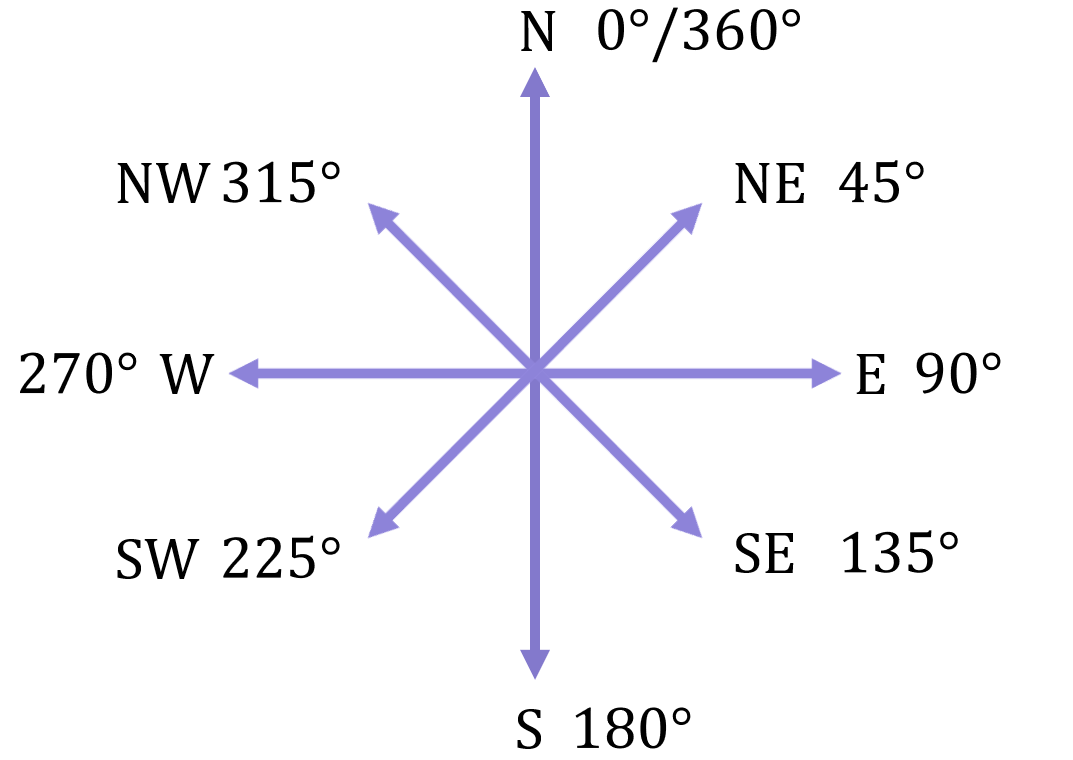
We can summarise this sytem as follows:
In mathematics, a bearing is defined as the angle (in degrees) measured clockwise from North.
Bearings are usually given as a three-figure bearing, so for example 45^\circ clockwise from North (i.e. the NE direction) would usually be stated as a bearing of 045^\circ. 90^\circ clockwise from North (i.e. E direction) would usually be stated as a bearing of 090^\circ, and so on. Once the bearing goes into three figures naturally, like say the SE direction (a bearing of 135^\circ), you no longer have to add the extra 0 at the beginning.
Bearings questions all involve applying your knowledge of either the Sine or Cosine Rule, plus related angles relationships. Questions typically come in one of two forms: the simpler style will provide a diagram for you to work with; the harder style will only have a written description of a scenario and you’ll have to come up with the diagram yourself.
Before starting this topic, it is useful to recall some key sketching tips. When doing bearings questions, it is often useful to:
- Draw on North reference lines at all vertices (i.e. corners); and
- Extend existing lines of the diagram to create related angles shapes.
Question Style 1 – Diagram Provided
Jen begins her journey at a hostel (H) and walks for 4km on a bearing of 015^\circ to her lunch stop (L). She then walks on a bearing of 110^\circ for 5.2km until she reaches the campsite (C). A diagram of her journey is provided below:
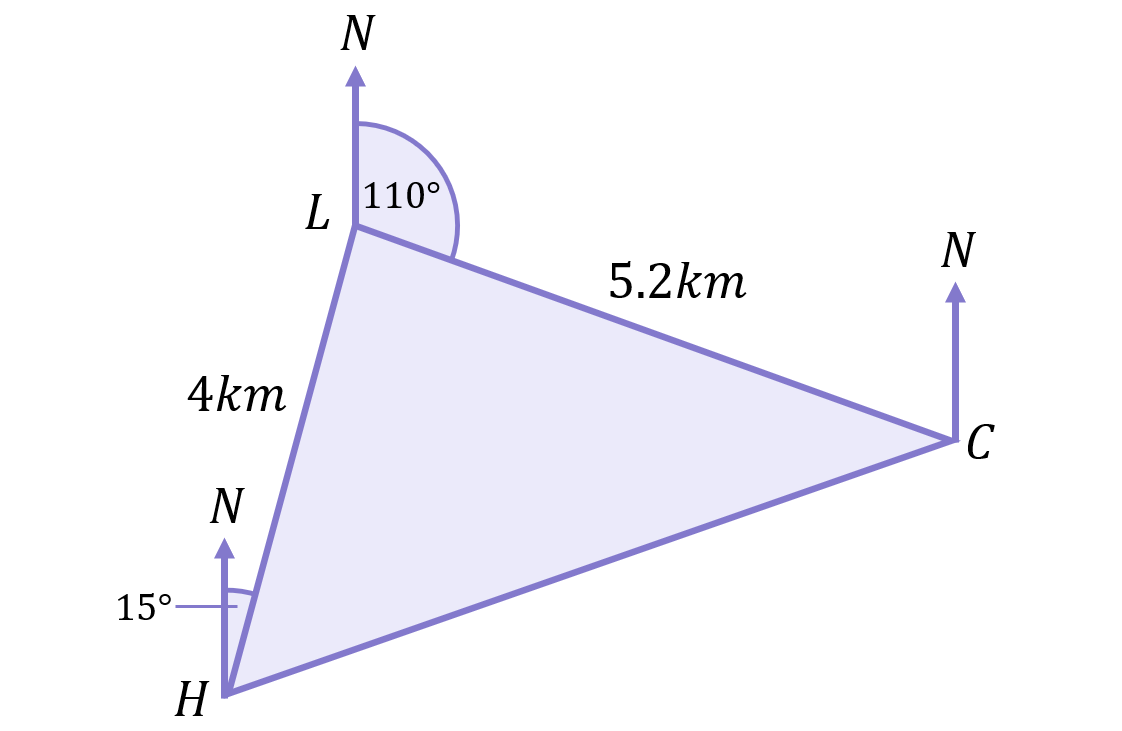
a) What is the bearing of the hostel (H) from the lunch stop (L)?
b) After staying overnight at the campsite (C), what distance and on what bearing does Jen need to walk to get back to the hostel (H)?
a) In simpler language, this question is just asking: in what direction do you need to walk to get from L back to H? Clearly you know the distance is 4km, but that’s not much use if you don’t know the right direction!
We can answer this using related angles only – no need for the Sine or Cosine Rule just yet!
We can extend the tail of the North line at L downward (effectively drawing a South line). Because the two North lines are parallel, this creates a Z shape:
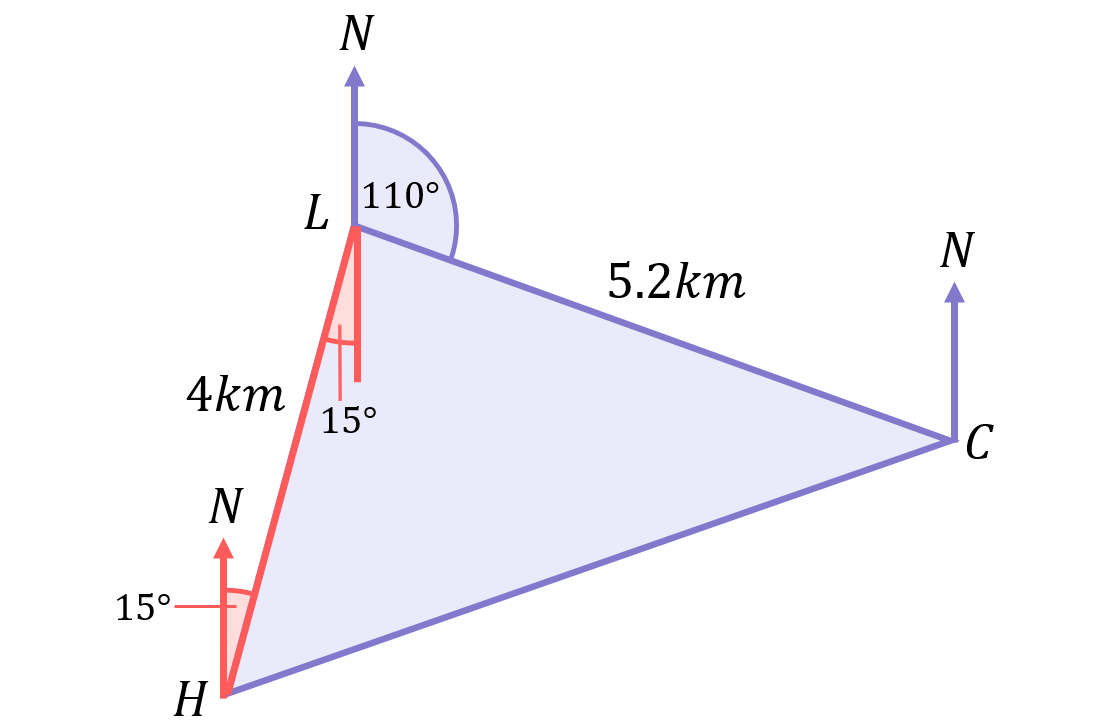
The North line is a straight line (of course) and all angles along a straight line add up to 180^\circ. Therefore, the “gap” left at L must be 70^\circ:
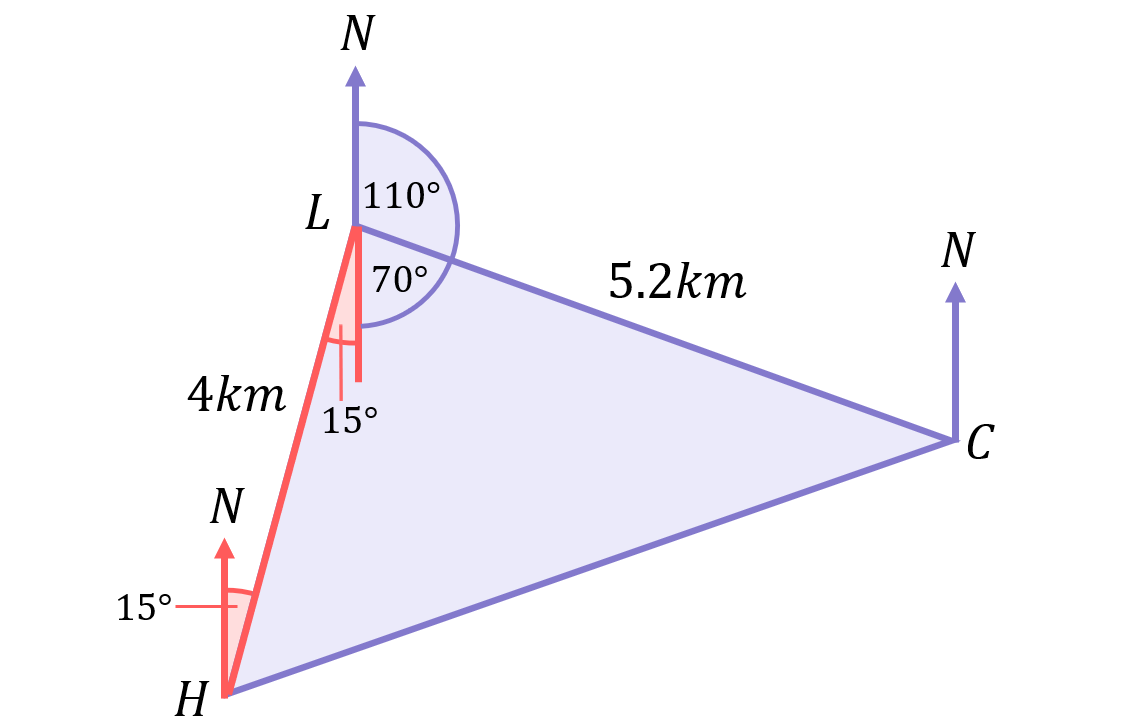
Having come this far, it should be pretty clear that the angle inside the triangle at L is 85^\circ (70^\circ+15^\circ):
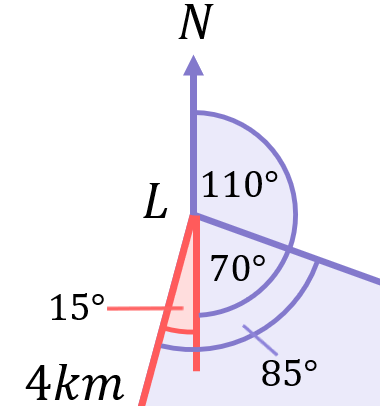
And therefore, including the 110^\circ, the overall bearing required is 195^\circ (110^\circ+85^\circ):
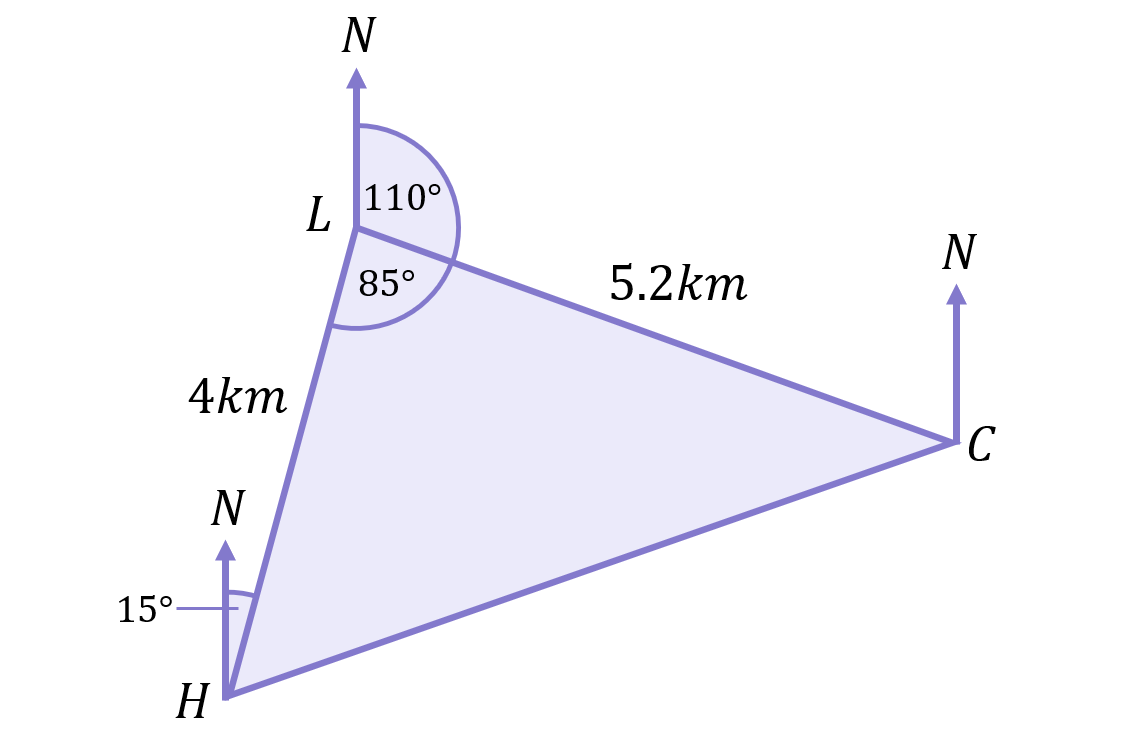
A: The hostel (H) is on a bearing of 195^\circ from the lunch stop (L).
b) This question is a bit more challenging as there’s more we need to work out. Currently, we don’t know either the distance or direction required to get from the campsite (C) back to the hostel (H), so we’ll have to work out both. Following the last question, we now have a bit more information in our starting diagram:
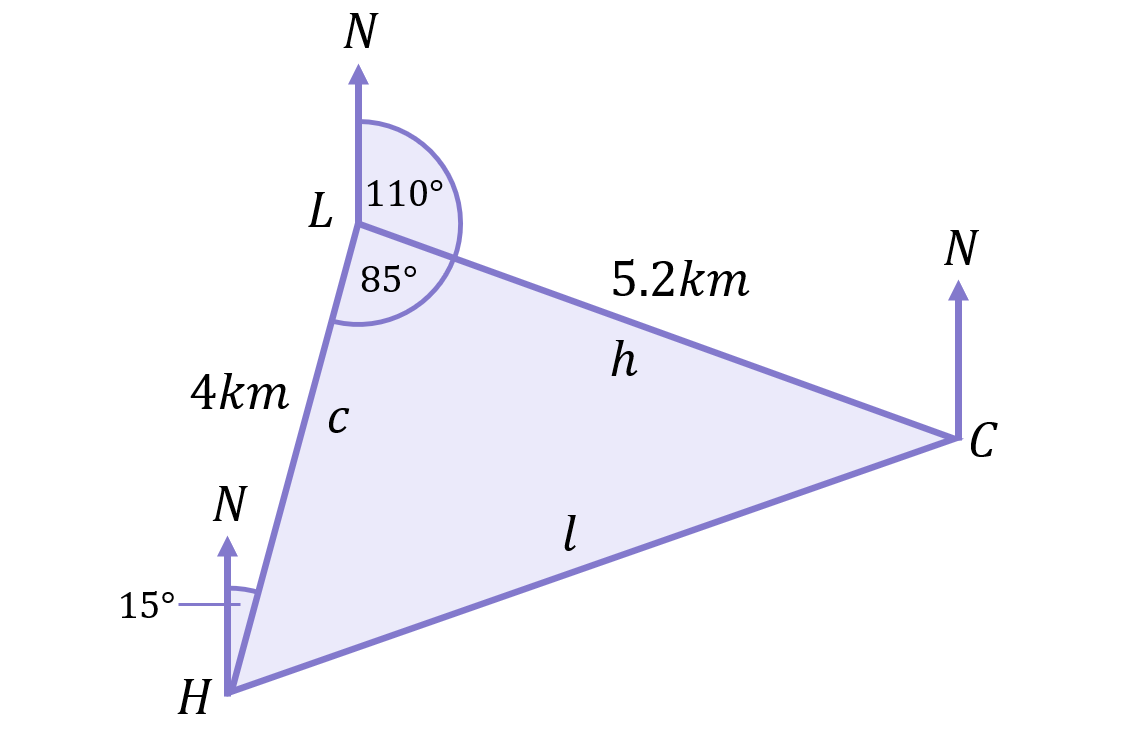
(I’ve also added in the side labels according to the usual labelling convention)
Recall Form 1 of the Cosine Rule:
a^{2}=b^{2}+c^{2}-2bc\cos{A}
As you know by now, Form 1 of the Cosine Rule can be used to calculate the remaining side of a non-right-angled triangle assuming the two other sides of the triangle, plus the included angle, are known. We know both side c and side h, plus the angle L=85^\circ in between, so we can use Form 1 of the Cosine Rule to work out the remaining side l:
\begin{aligned}l^{2}&=c^{2}+h^{2}-2ch\cos{L} \\[12pt]l^{2}&=(4)^{2}+(5.2)^{2}-2(4)(5.2)\cos{85} \\[12pt]l^{2}&=16+27.04-41.6(0.087) \\[12pt]l^{2}&=39.4 \\[12pt]l&=\sqrt{39.4} \\[12pt]l&=6.3km\end{aligned}
We’re halfway there – we now know that the distance from the campsite (C) back to the hostel (H) is 6.3km, but we still need the direction:
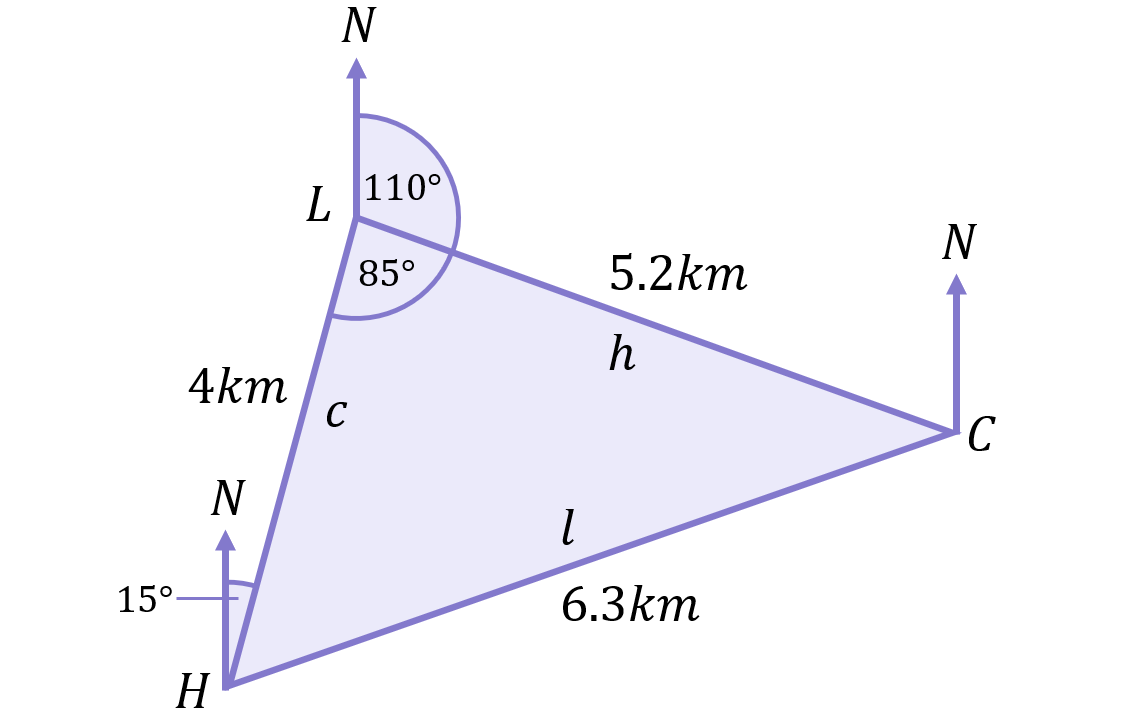
Recall that the Sine Rule can be used when one corresponding side and angle pair is known, plus one additional piece of information. Since we know both side l and angle L (the corresponding pair), we can use the Sine Rule to work out the angle C:
\begin{aligned}\frac{c \checkmark}{\sin{C}}&=\frac{h}{\sin{H}}=\frac{l \checkmark}{\sin{L} \checkmark} \\[12pt]\frac{c}{\sin{C}}&=\frac{l}{\sin{L}} \\[12pt]l\sin{C}&=c\sin{L} \\[12pt]\sin{C}&=\frac{c\sin{L}}{l} \\[12pt]C&=\sin^{-1}\left(\frac{c\sin{L}}{l}\right)\\[12pt]C&=\sin^{-1}\left(\frac{(4)\sin{85}}{(6.3)}\right) \\[12pt]C&=\sin^{-1}(0.63) \\[12pt]C&=39.2^\circ\end{aligned}
Be very clear that this is not the bearing we need to follow to get from the campsite (C) back to the hostel (H) (although it is part of the answer). The actual bearing we need is highlighted green in the diagram below:
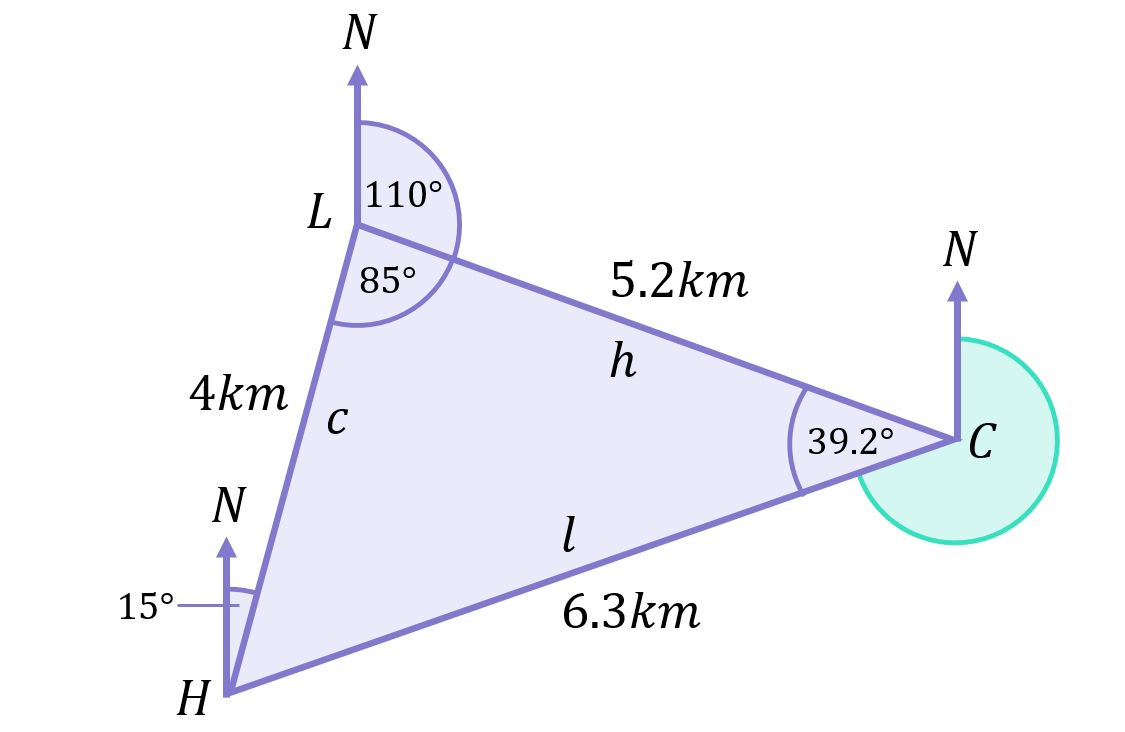
By extending the line from L to C, we can create an F shape:
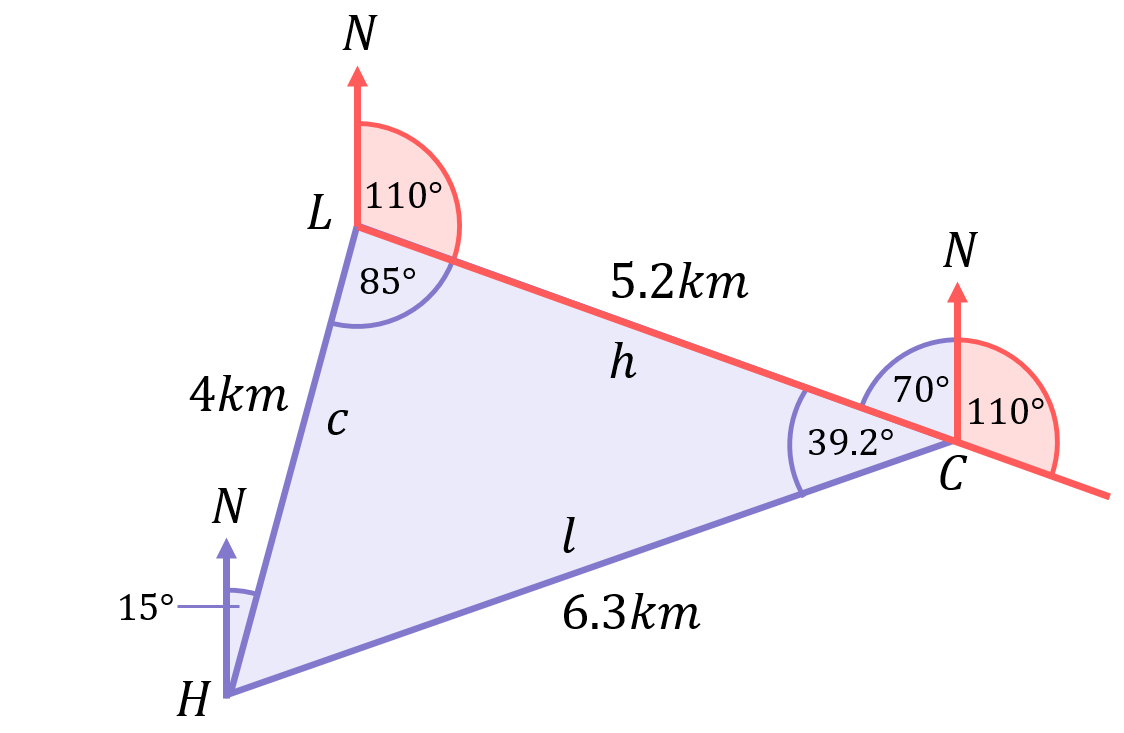
The 4 angles at C (relabelled w, x, y and z in the diagram below) clearly create a full circle (i.e. they all add up to 360^\circ):
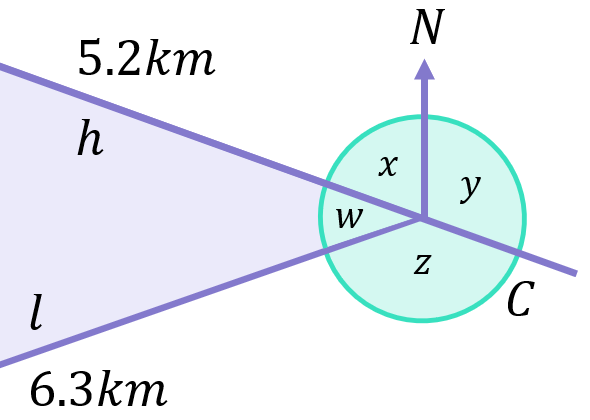
Given we know w=39.2^\circ, x=70^\circ and y=110^\circ, we can now calculate z:
\begin{aligned}w+x+y+z&=360^\circ \\[12pt]z&=360^\circ-w-x-y \\[12pt]z&=360^\circ-39.2^\circ-70^\circ-110^\circ \\[12pt]z&=140.8^\circ\end{aligned}
Now we can calculate the bearing we need to follow to get from the campsite (C) back to the hostel (H):
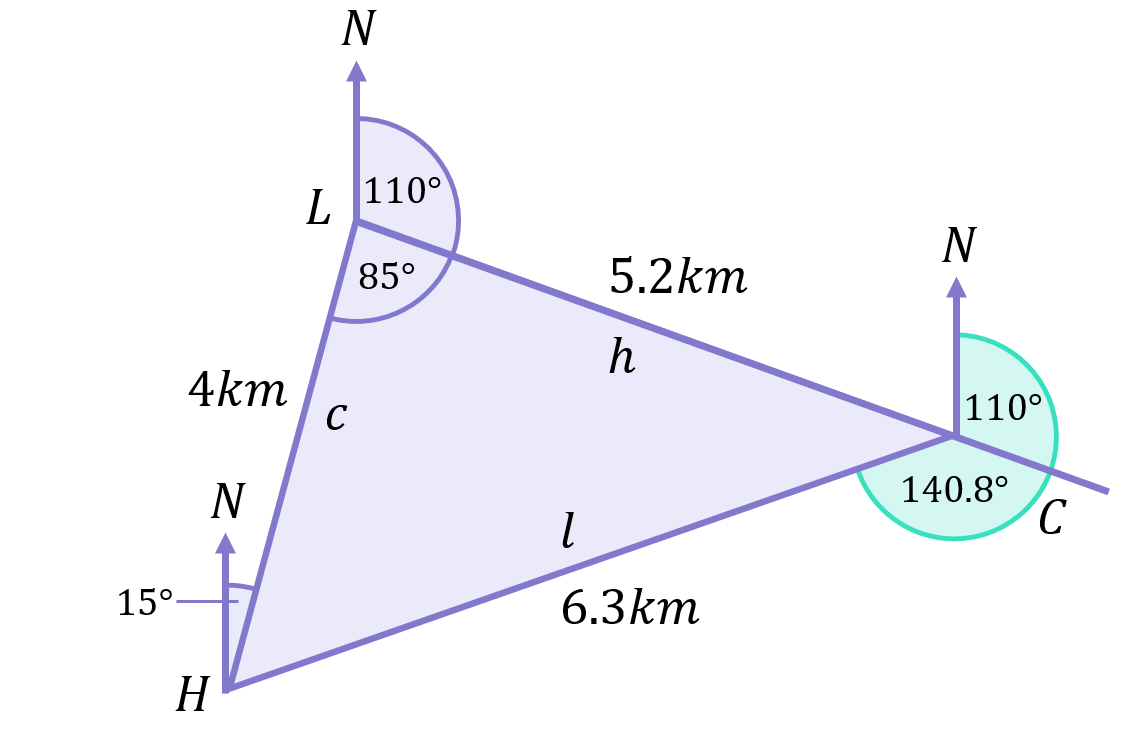
\begin{aligned}\text{Bearing from C to H}&=110^\circ+140.8^\circ \\[12pt]\text{Bearing from C to H}&=250.8^\circ\end{aligned}
Recall that the original question asked for both the distance and direction required to get back to the hostel; therefore, your final answer must state both pieces of information:
A: To return to the hostel (H) from the campsite (C), Jen must walk 6.3km on a bearing of 250.8^\circ.
Question Style 2 – Written Description (no diagram provided)
A competitor in an orienteering contest travels 2000m on a bearing of 330^\circ and then 1000m on a bearing of 260^\circ.
a) Draw a sketch of the route taken by the competitor.
b) How far must the competitor travel and on what bearing to return to his starting point?
a) Even if the question didn’t explicitly ask you to draw a sketch, it is always helpful to have one, so you should draw one anyway.
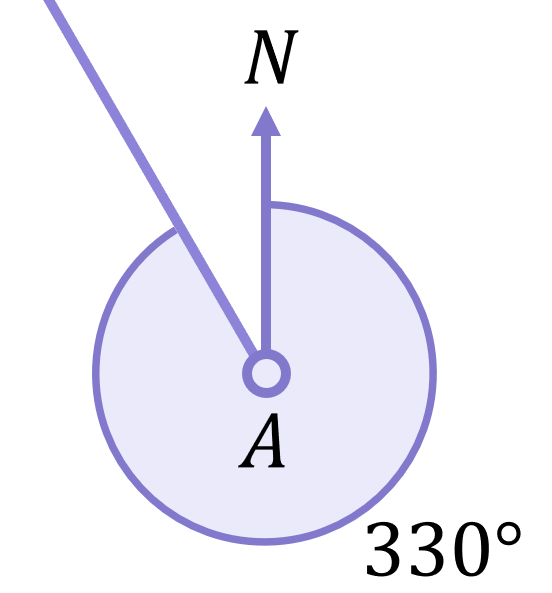
We will assume the competitor starts at point A, travels 2000m on a bearing of 330^\circ to point B, then travels 1000m on a bearing of 260^\circ to point C.
Choose a position to be the starting point A, then measure a 330^\circ angle using a protractor:
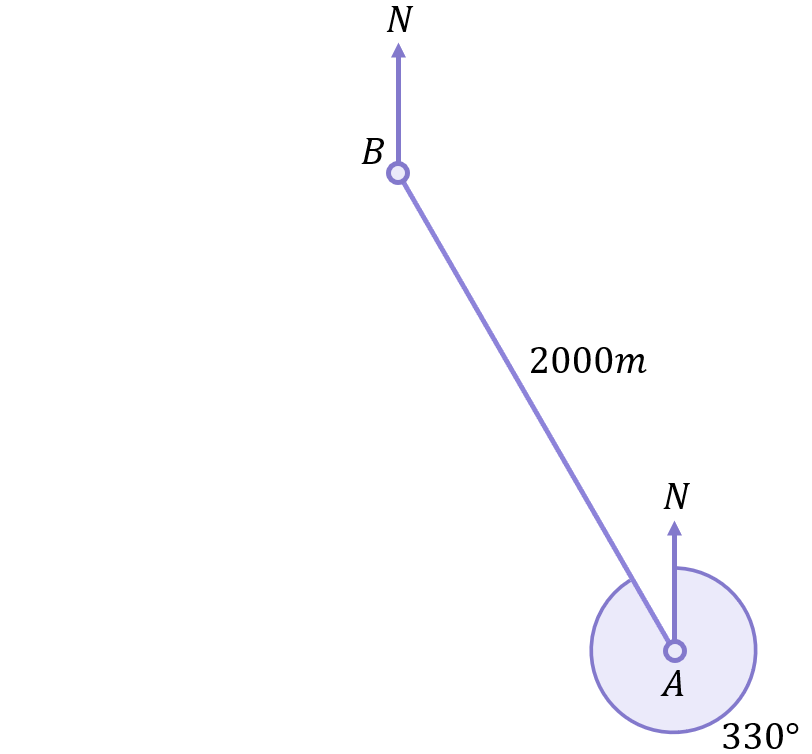
Extend this line using a suitable scale (such as 1cm:200m) until it is 2000m long, and draw on point B:
From point B, measure a 260^\circ angle using a protractor and draw a line 1000m long using the same scale to take you to point C:
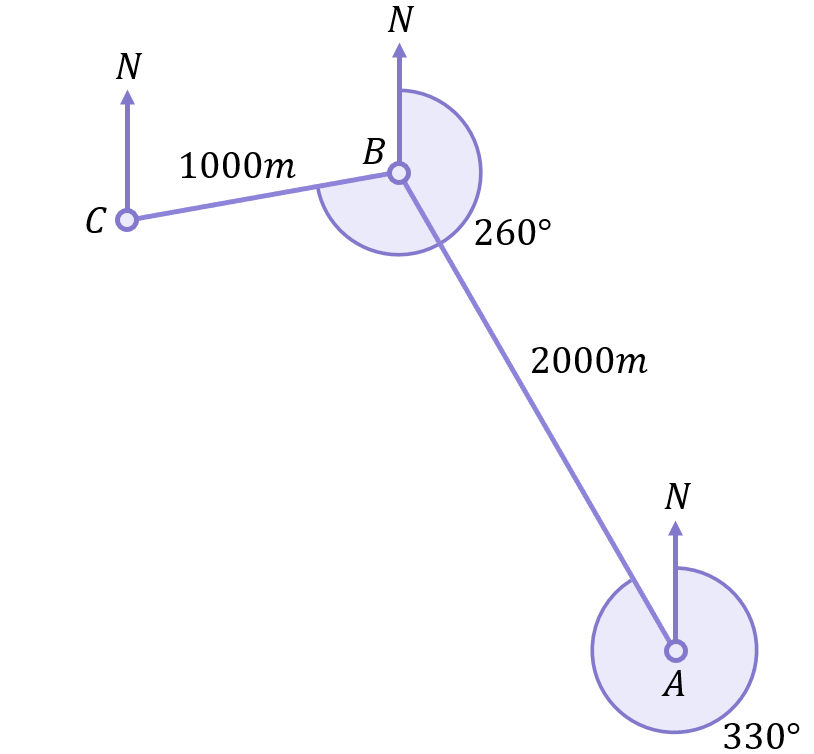
We don’t know the distance or bearing necessary to return to point A from point C (part (b) of this question wants you to figure that out), so we will just connect these points with a straight line for now to finish the route:
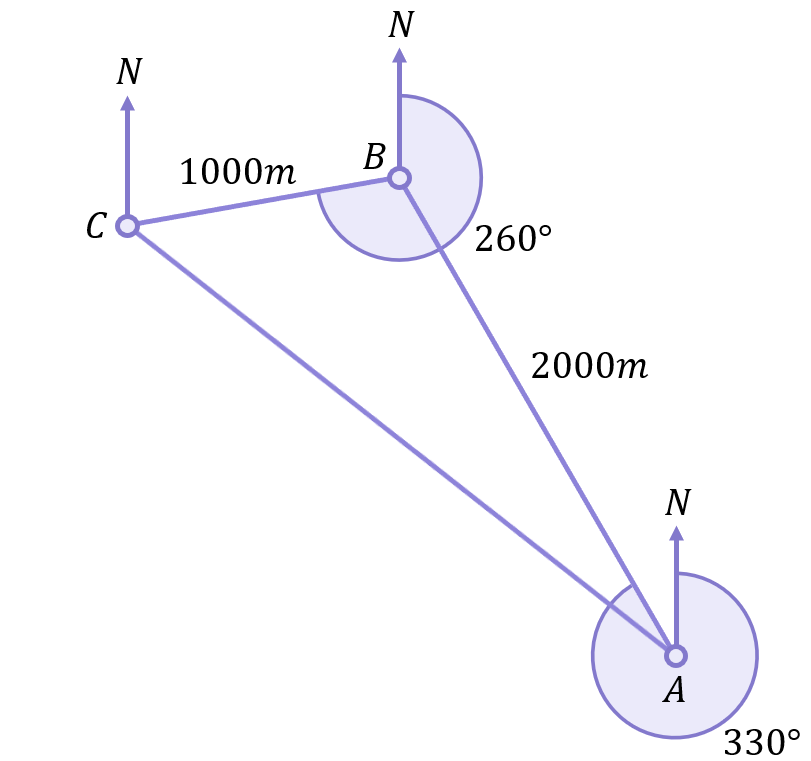
b) The diagram of the route has formed a non-right-angled triangle, but currently we only know 2 pieces of information about it (the lengths of sides a and c). Remember, you always need at least 3 pieces of info to be able to use either the Sine or Cosine Rule. Before trying to use these rules then, we must use our knowledge of related angles to work out more information about the triangle.
As is often the case, extending the lines of the diagram will help with this. Extending the line from point A to point B produces a clear F shape:
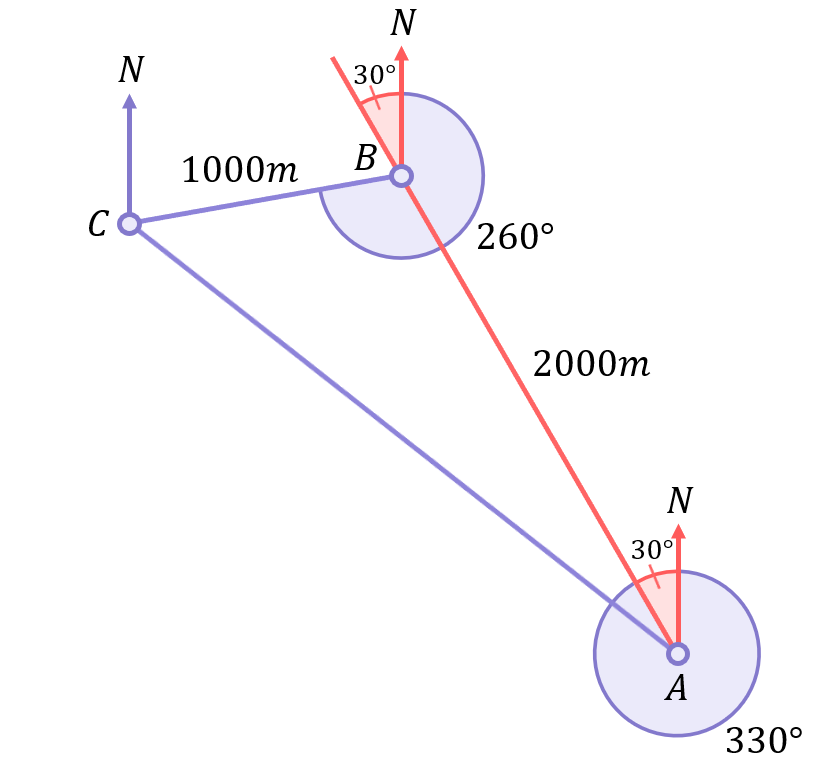
Focusing in on point B:
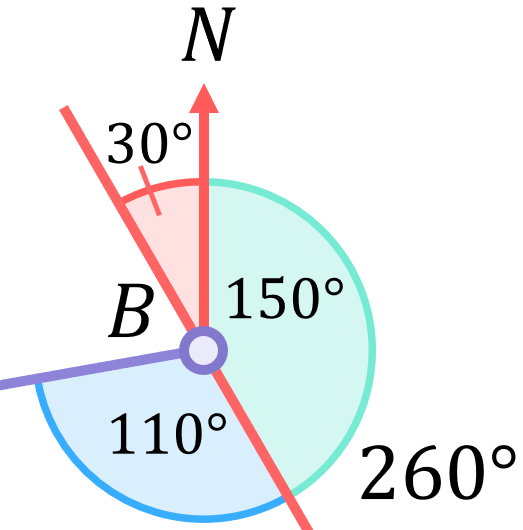
The angle at the “other side” of the North line (highlighted green above) must be 150^\circ since the angles along the straight line (in red) will always add to 180^\circ.
Further, since the original bearing at point B was 260^\circ, then the angle highlighted green plus the angle highlighted blue must add to 260^\circ. The blue angle (the angle inside the triangle that we are trying to determine) must therefore be 260^\circ-150^\circ=110^\circ.
Notice that we now know 2 sides (sides a and c) plus an included angle (B=110^\circ):
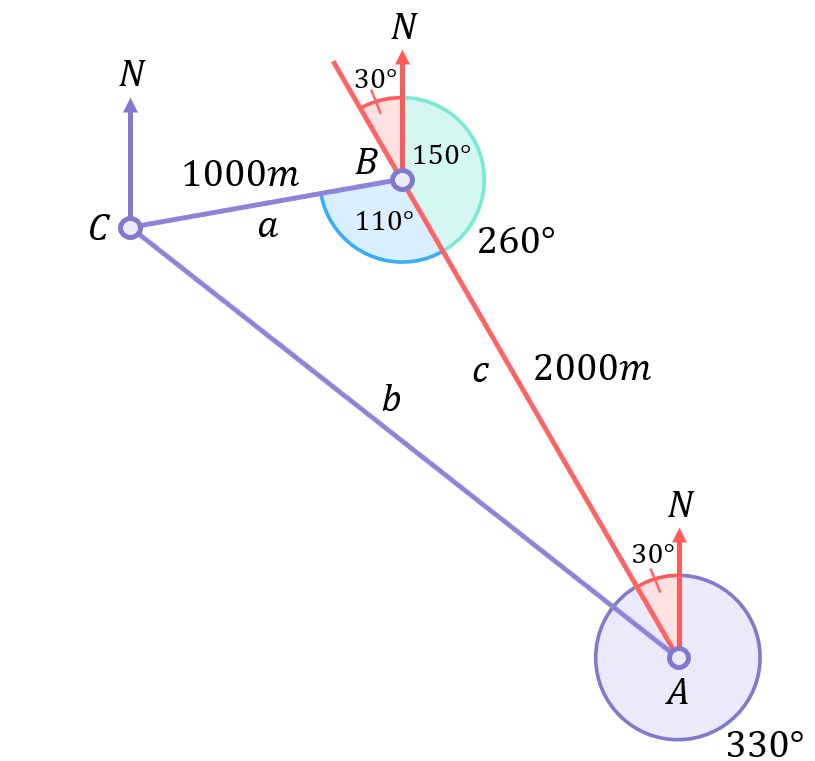
We can therefore use Form 1 of the Cosine Rule to calculate side b:
\begin{aligned}b^{2}&=a^{2}+c^{2}-2ac\cos{B} \\[12pt]b^{2}&=(1000)^{2}+(2000)^{2}-2(1000)(2000)\cos{110} \\[12pt]b^{2}&=1,000,000+4,000,000-4,000,000(-0.34) \\[12pt]b^{2}&=6,368,081 \\[12pt]b&=\sqrt{6,368,081} \\[12pt]b&=2,524m\end{aligned}
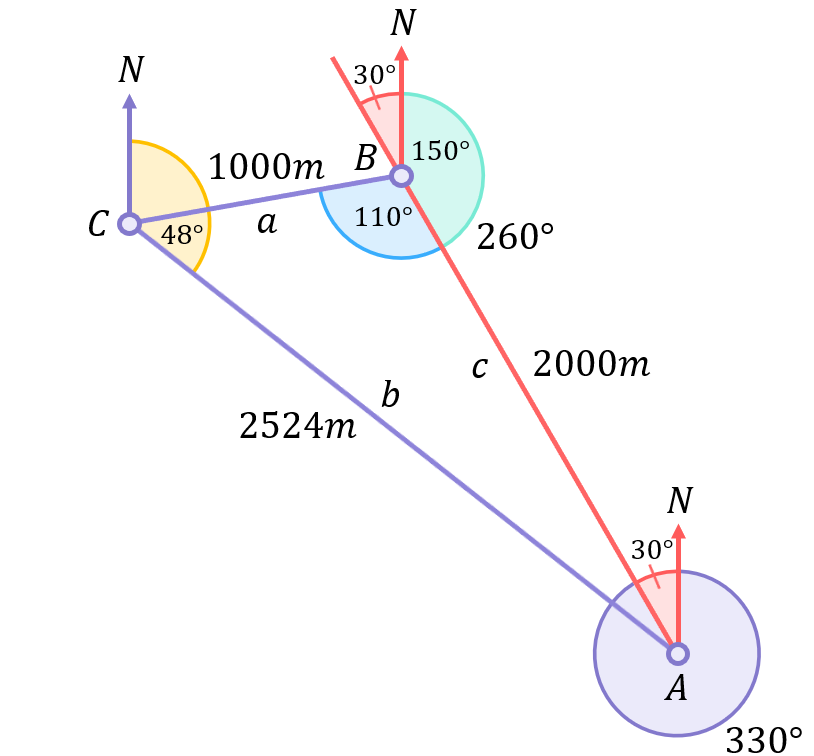
We’re halfway there – we now know that the distance from point C to point A is 2,524m, but we still need the direction.
Since we now know all 3 sides of the triangle, we can use Form 2 of the Cosine rule to calculate the angle inside the triangle at point C:
\begin{aligned}\cos{C}&=\frac{a^{2}+b^{2}-c^{2}}{2ab} \\[12pt]\cos{C}&=\frac{(1000)^{2}+(2524)^{2}-(2000)^{2}}{2(1000)(2524)} \\[14pt]\cos{C}&=\frac{3,370,576}{5,048,000} \\[12pt]\cos{C}&=0.6687 \\[12pt]C&=\cos^{-1}(0.6687) \\[12pt]C&=48^\circ\end{aligned}
As in the previous example, be very clear that this is not the bearing we need to follow to get from point C back to point A. 48^\circ is part of the answer, but the actual bearing we need is highlighted in gold in the diagram below:
The “missing” angle at point B must be 70^\circ since all the angles at point B collectively form a circle and therefore add to 360^\circ:
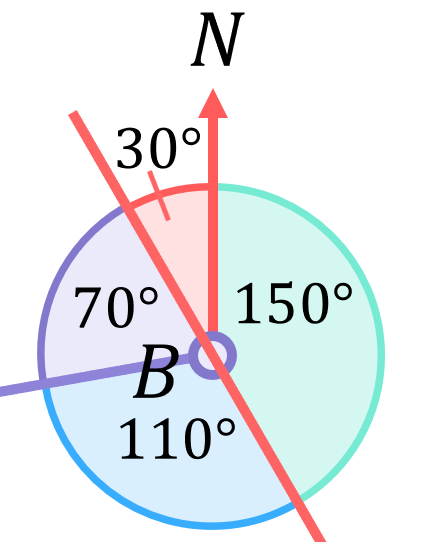
The purple and red angles above add to 70^\circ+30^\circ=100^\circ. Removing some unnecessary detail from the last part of this question, if we now extend the line from point C to point B it produces a clear F shape:
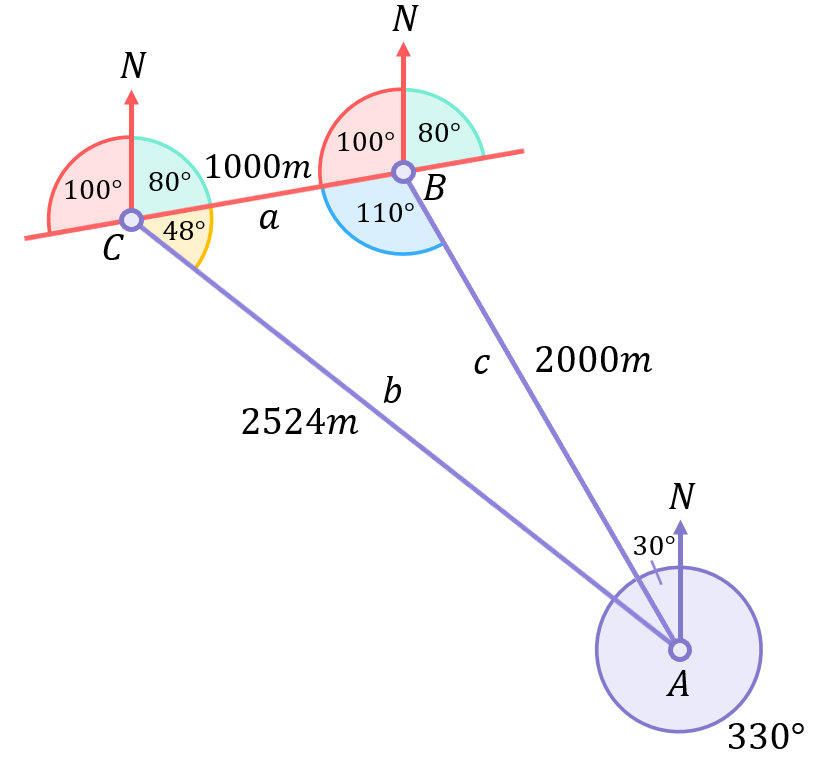
The angles at the “other side” of the North lines at points B and C (highlighted green above) must be 80^\circ since the angles along the straight line (in red) will always add to 180^\circ.
Looking at our final diagram above, it is clear the bearing we need to go from point C back to point A is the 80^\circ (in green) plus the 48^\circ (in gold):
\begin{aligned}\text{Bearing from C to A}&=80^\circ+48^\circ \\[12pt]\text{Bearing from C to A}&=128^\circ\end{aligned}
Recall that the original question asked for both the distance and direction required to get back to the starting point; therefore, your final answer must state both pieces of information:
A: To return to the starting point at A, the competitor must walk 2,524m on a bearing of 128^\circ.
Key Outcomes
In mathematics, a bearing is defined as the angle in degrees measured clockwise from North.
Bearings are always stated using three figures. For example, 90^\circ should be written as 090^\circ. If the bearing already has three figures, like say 120^\circ, you do not need to change this.
In bearings questions, adding certain elements to a given diagram can make opportunities to use related angles more obvious. The two most common ways of doing this are:
- Drawing on North reference lines at all vertices (i.e. corners); and
- Extending the existing lines of the diagram