Area is the amount of space inside the boundary of a flat (i.e. 2-dimensional) object.

By this stage you will be familiar with calculating the areas of most standard shapes, but the key area formulas you should know are given below as a reminder:

A composite area, sometimes called a “compound shape”, is a shape that can be split up into several simpler, standard geometric figures such as squares, rectangles, triangles, circles, etc.

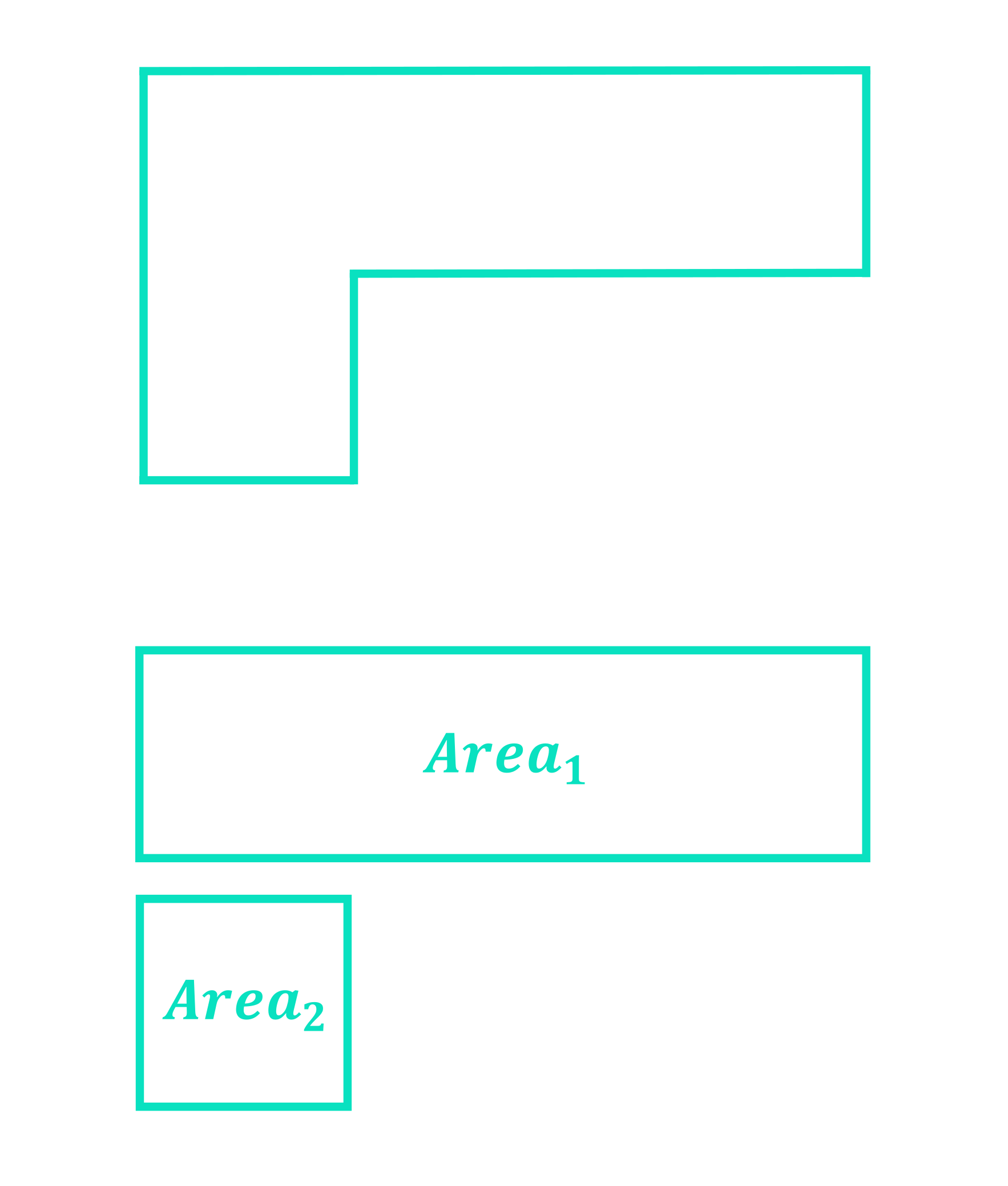
Take for example the typical garden shed shown below:

Suppose the front face of the shed had the following dimensions:

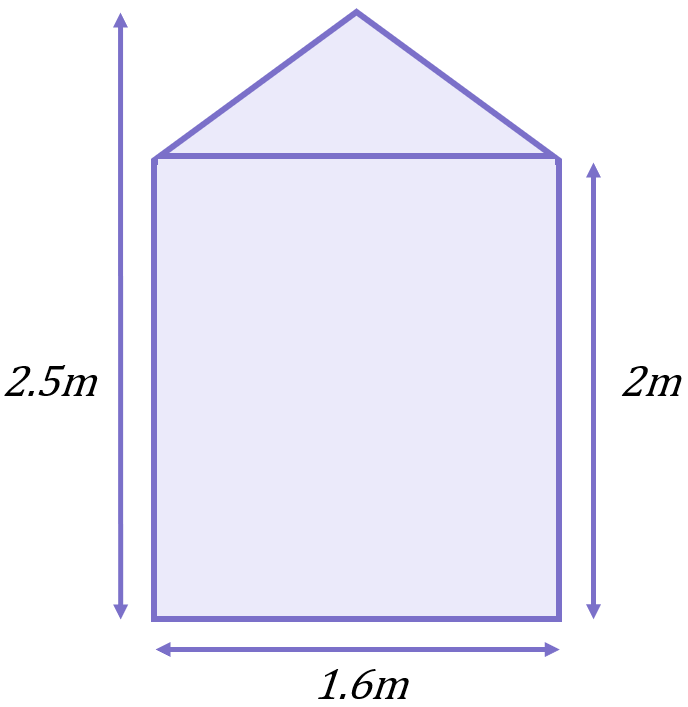
If you were asked to paint the front of the shed, you’d need to know how many square metres of paint to use. In other words, you’d need to know the area of the face of the shed. So how would you calculate the area of the face, considering it’s not a standard shape? If the shed was a simple rectangular shape, or a simple triangular shape, you could easily work out the area using the standard area formulae you know well. But this shape is neither a rectangle nor a triangle – it has elements of both:

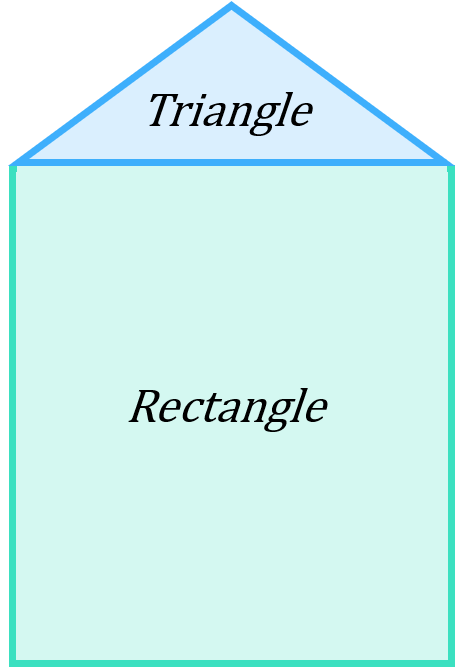
If we split the shape up into a rectangle and a triangle, we can work out the areas of the individual shapes and add them together to get the total area:

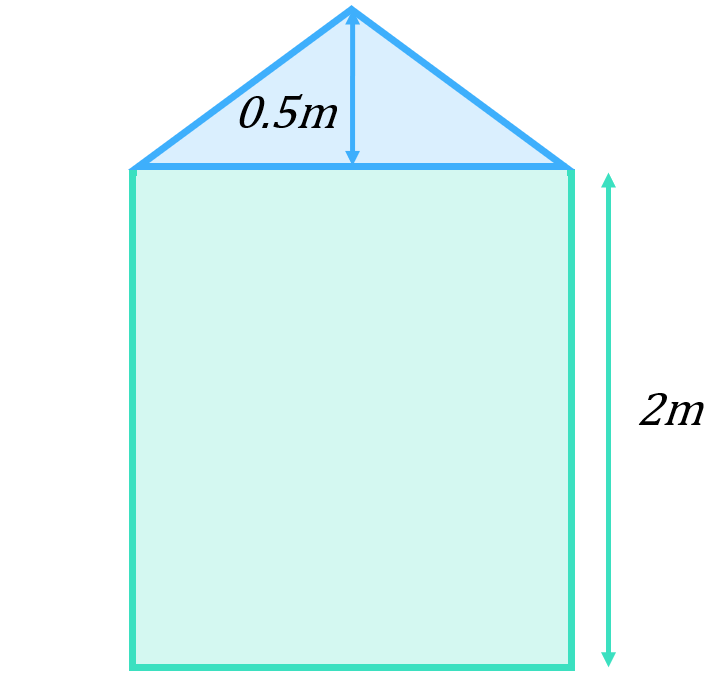
\begin{aligned}\text{Area of rectangle}&=l\times b \\[12pt]\text{Area of rectangle}&=2\times 1.6 \\[12pt]\text{Area of rectangle}&=3.2m^{2}\end{aligned}

\begin{aligned}\text{Area of triangle}&=\frac{1}{2}bh \\[12pt]\text{Area of triangle}&=\frac{1}{2}(1.6)(0.5) \\[12pt]\text{Area of triangle}&=0.4m^{2}\end{aligned}

\begin{aligned}\text{Total area}&=\text{Area of rectangle}+\text{Area of triangle} \\[12pt]\text{Total area}&=3.2m^{2}+0.4m^{2} \\[12pt]\text{Total area}&=3.6m^{2}   \end{aligned}

Find the area of the following composite figure:

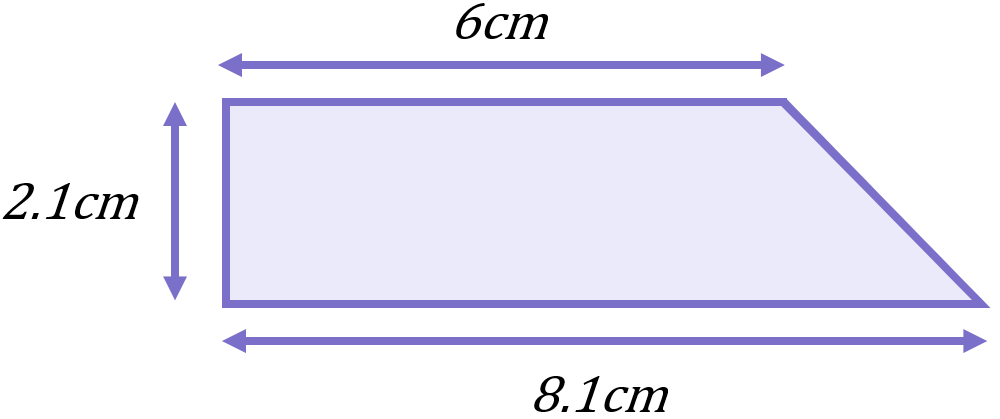
We can split this shape into a rectangle and a right-angled-triangle, and work out the area of each to get to the total area:

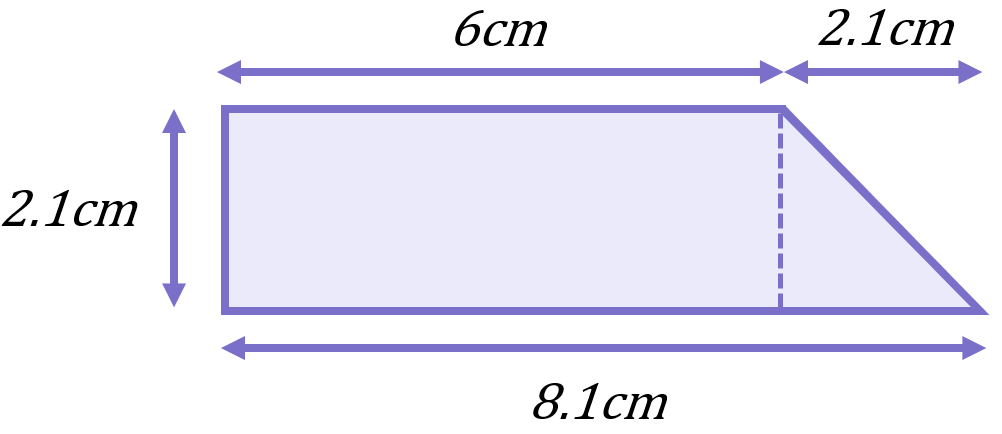
\begin{aligned}\text{Area of rectangle}&=l\times b \\[12pt]\text{Area of rectangle}&=6\times 2.1 \\[12pt]\text{Area of rectangle}&=12.6cm^{2}\end{aligned}

\begin{aligned}\text{Area of triangle}&=\frac{1}{2}bh \\[12pt]\text{Area of triangle}&=\frac{1}{2}(2.1)(2.1) \\[12pt]\text{Area of triangle}&=2.2cm^{2}\end{aligned}

\begin{aligned}\text{Total area}&=\text{Area of rectangle}+\text{Area of triangle} \\[12pt]\text{Total area}&=12.6cm^{2}+2.2cm^{2} \\[12pt]\text{Total area}&=14.8cm^{2}   \end{aligned}

Determine the area of the object shown below:

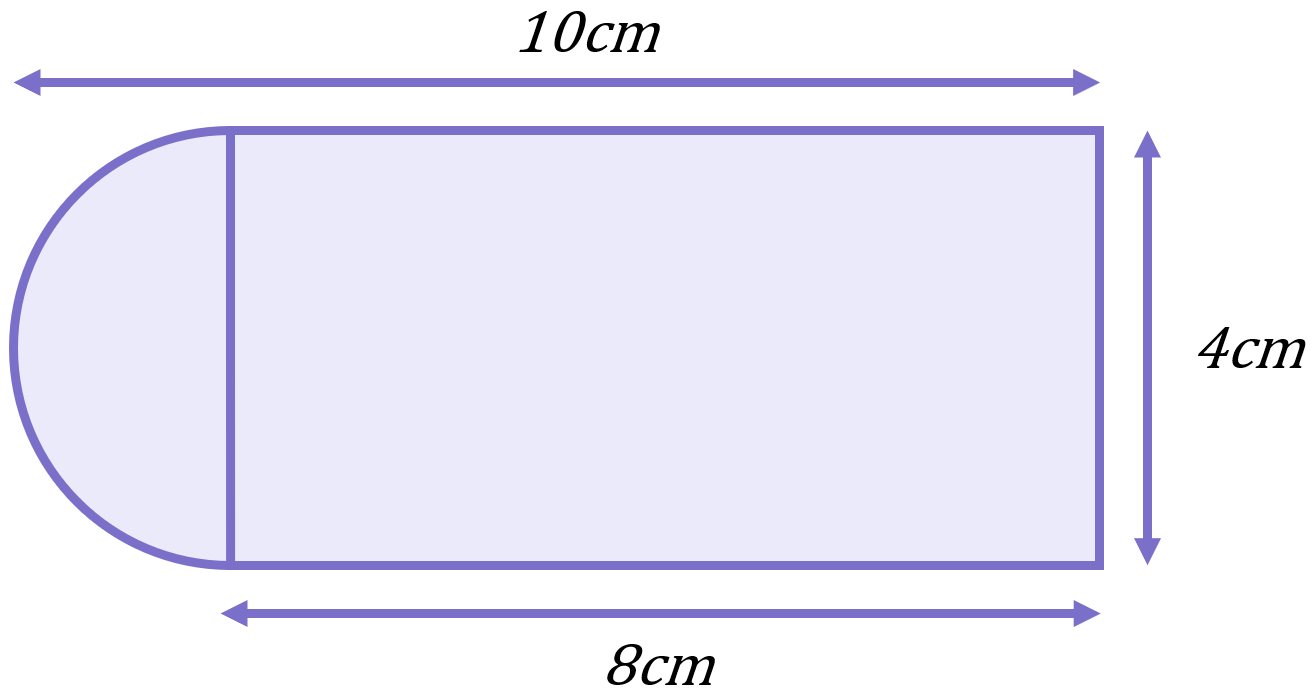
This composite figure is made up of a rectangle (8cm by 4cm) and a semicircle of radius 2cm:

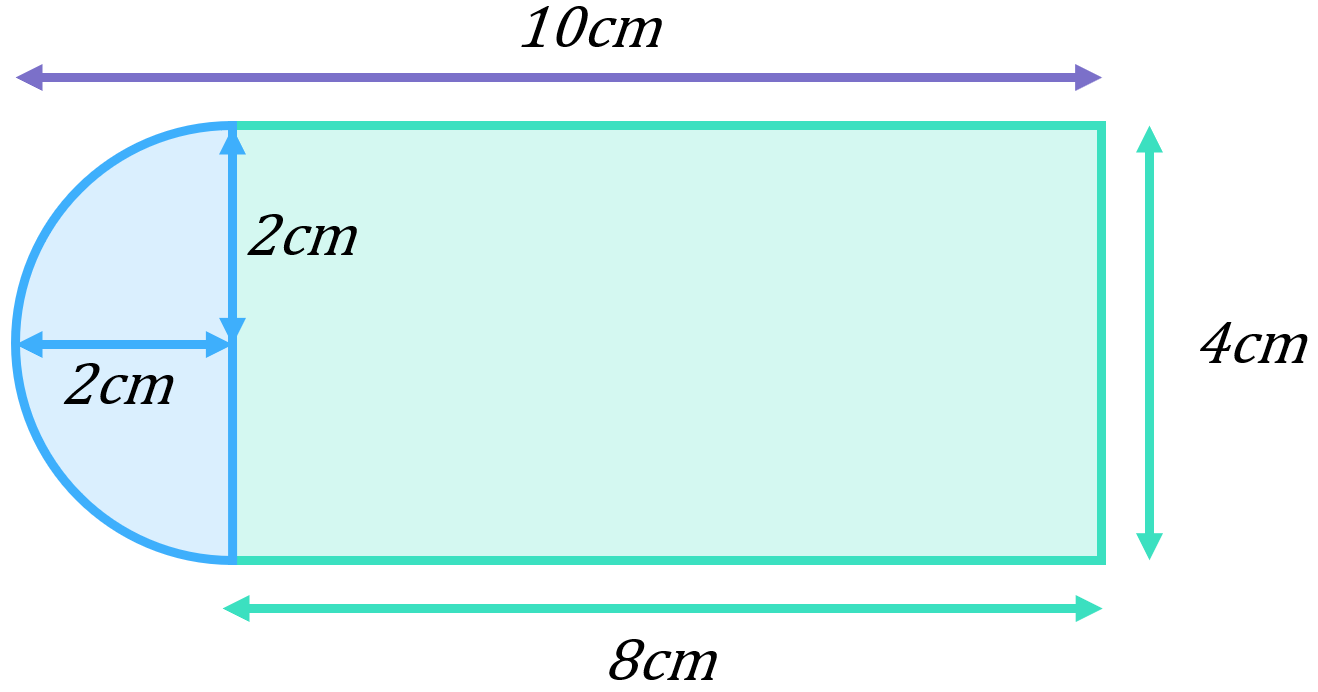
\begin{aligned}\text{Area of rectangle}&=l\times b \\[12pt]\text{Area of rectangle}&=8\times 4 \\[12pt]\text{Area of rectangle}&=32cm^{2}\end{aligned}

\begin{aligned}\text{Area of semicircle}&=\frac{\pi r^{2}}{2} \\[12pt]\text{Area of semicircle}&=\frac{\pi (2)^{2}}{2} \\[12pt]\text{Area of semicircle}&=6.3cm^{2}\end{aligned}

\begin{aligned}\text{Total area}&=\text{Area of rectangle}+\text{Area of semicircle} \\[12pt]\text{Total area}&=32cm^{2}+6.3cm^{2} \\[12pt]\text{Total area}&=38.3cm^{2}   \end{aligned}

A windscreen wiper on a car clears an area of rain like shown:

The area cleared by one wiper is shaded purple in the diagram below:

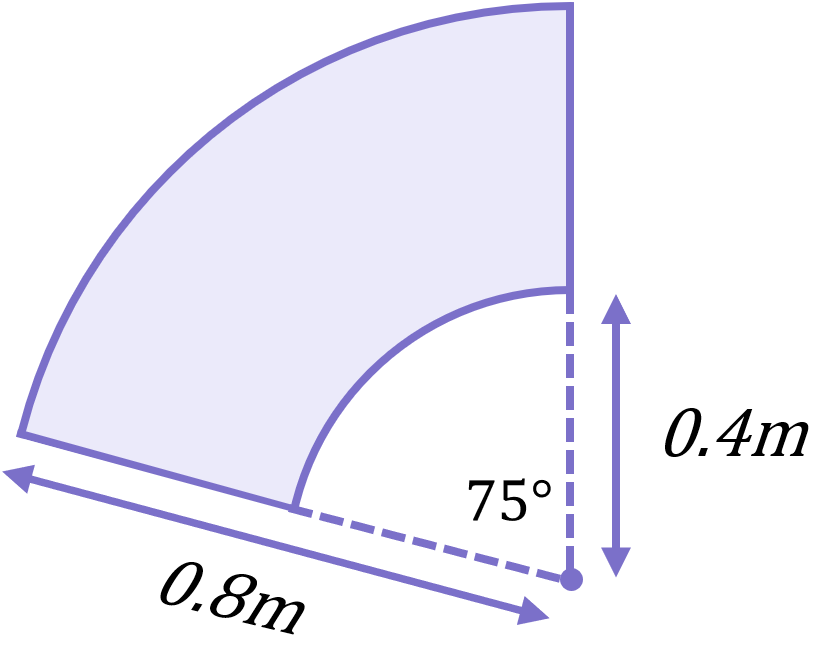
Calculate the area cleared by one wiper.

This is a much more challenging question requiring some out-of-the-box thinking. It’s not the easiest to spot at first, but this diagram can be thought of as two sectors overlapping each other:

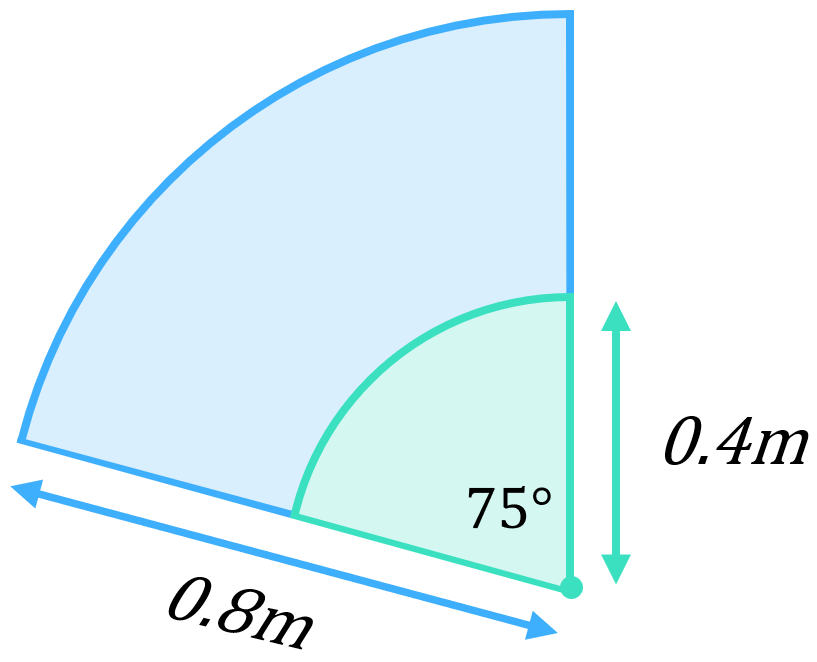
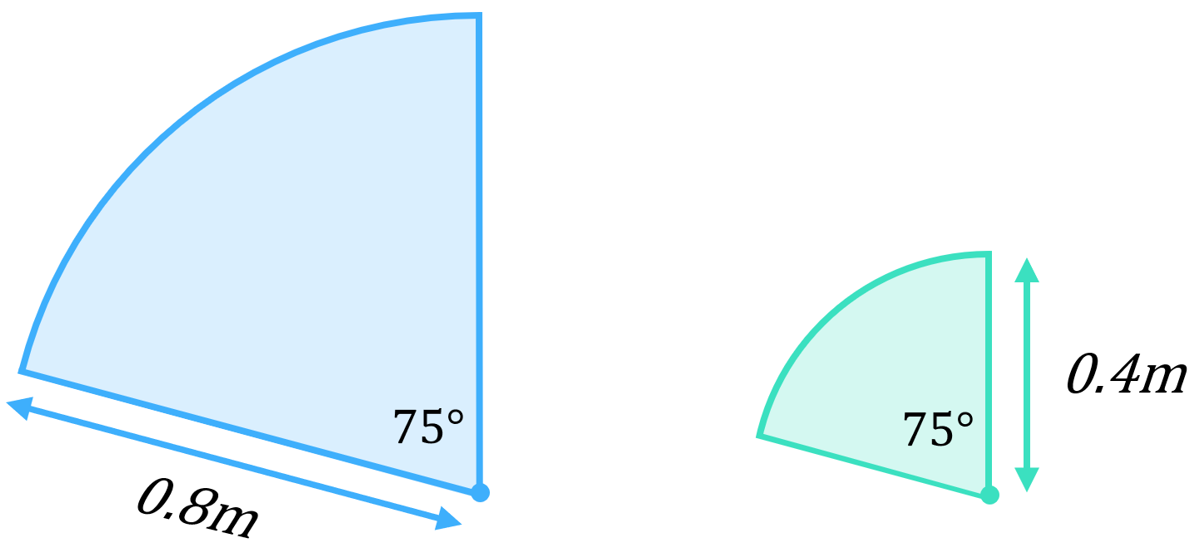
If we calculate the area of the larger sector (blue) and subtract the area of the smaller sector (green), we will be left with the area cleared by one wiper (the purple area in the original diagram):

\begin{aligned}\text{Area of blue sector}&=\frac{x}{360}\times\pi r^{2} \\[12pt]\text{Area of blue sector}&=\frac{75}{360}\times\pi (0.8)^{2} \\[12pt]\text{Area of blue sector}&=0.42m^{2}\end{aligned}

\begin{aligned}\text{Area of green sector}&=\frac{x}{360}\times\pi r^{2} \\[12pt]\text{Area of green sector}&=\frac{75}{360}\times\pi (0.4)^{2} \\[12pt]\text{Area of green sector}&=0.105m^{2}\end{aligned}

\begin{aligned}\text{Area cleared by wiper}&=\text{Area of blue sector}-\text{Area of green sector} \\[12pt]\text{Area cleared by wiper}&=0.42m^{2}-0.105m^{2} \\[12pt]\text{Area cleared by wiper}&=0.315m^{2}\end{aligned}