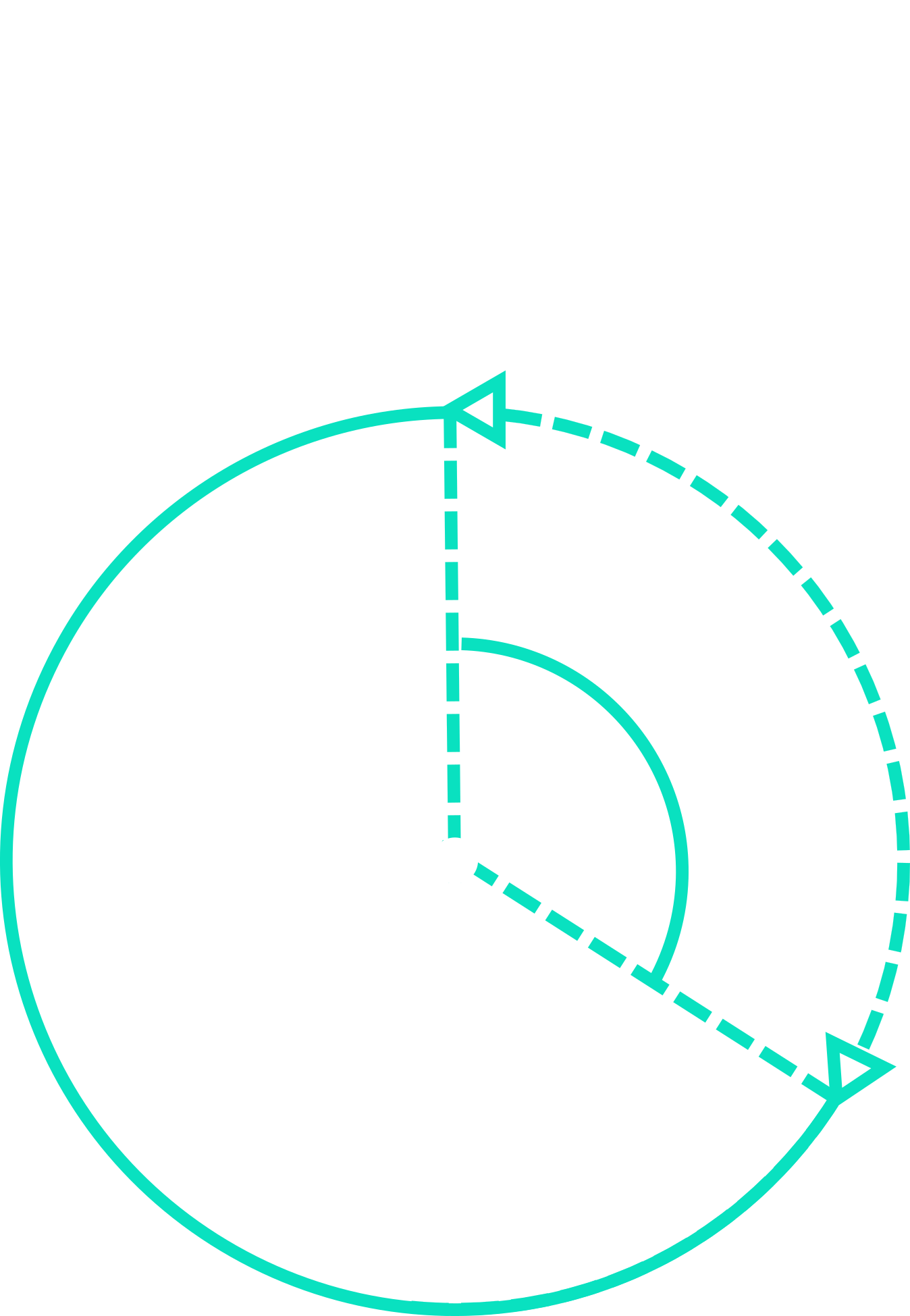
Area of a Sector
Of all the standard shapes we work with in National 5, the circle is the only one with curved edges. This affects the geometry of the shape quite considerably and gives circles some unique characteristics.
Before we get into this topic, it is useful to recall the definitions of various aspects of a circle’s geometry which should all be familiar:
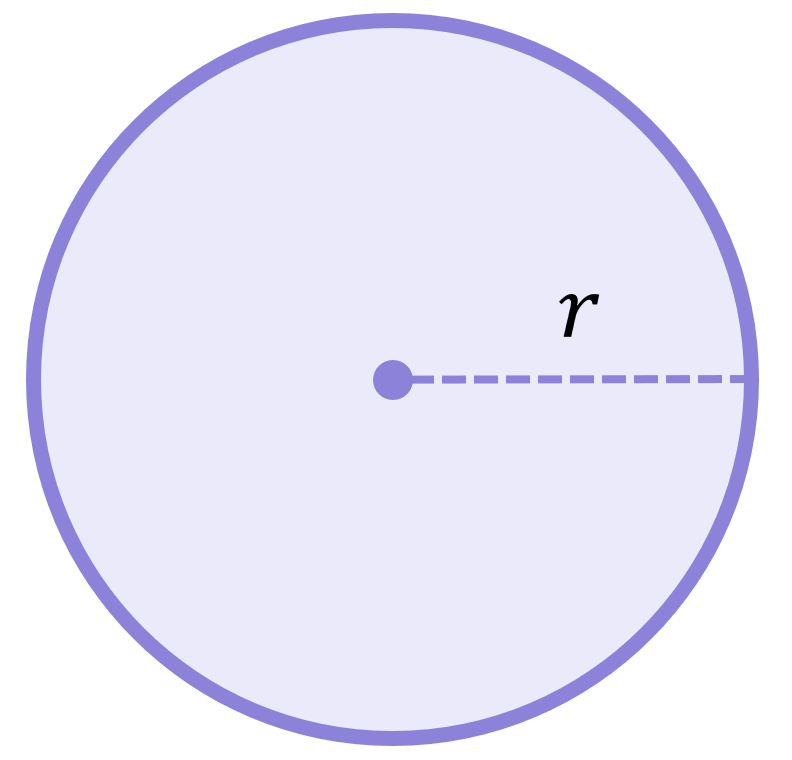
The radius is any straight line going from the centre of a circle to any point on its circumference:
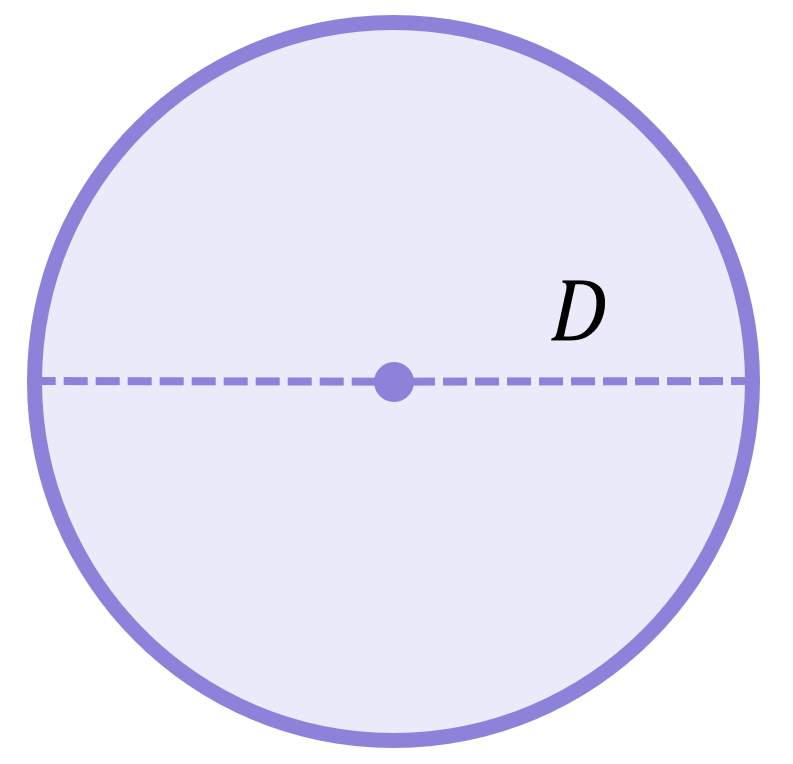
The diameter is any straight line passing through the centre of a circle whose ends both touch the circle’s circumference. A circle’s diameter is always double the length of its radius:
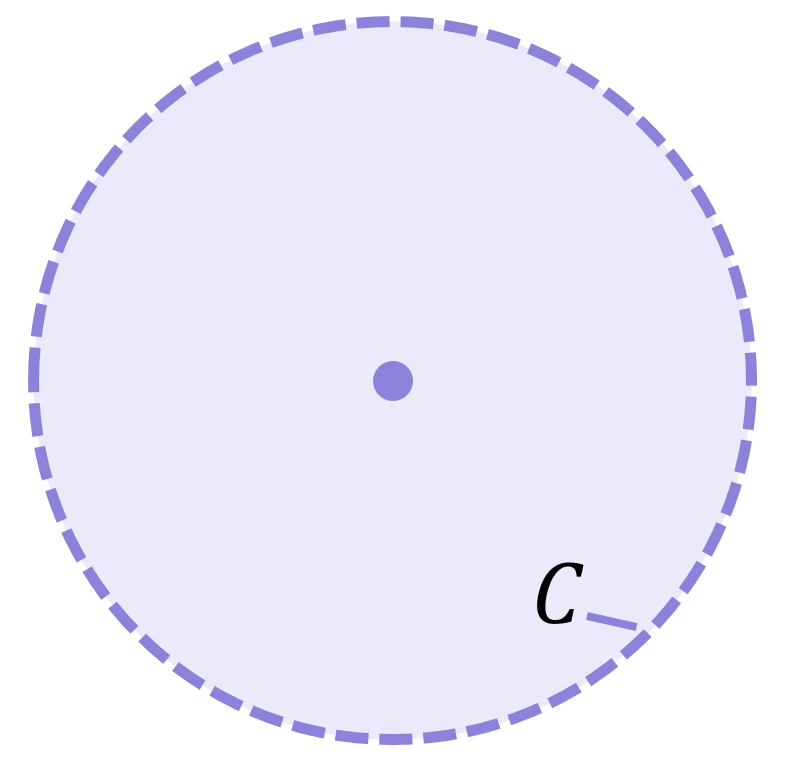
The circumference is the distance around the edge of a circle (in non-curved shapes, this is called the perimeter):
A chord is any line connecting two points on a circle’s circumference that does not pass through the centre of the circle. If the line passed through the centre, it would be a diameter (i.e. the diameter is a special chord):
An arc is any small section of the circumference of a circle:
A sector is the region bounded by two radii and an arc. It is small section of the circle’s overall area. For simplicity, you can think of this as a “pizza slice” shape:
A segment is the region bounded by a chord and an arc:
And you will already be very familiar with the formulas for the area and circumference of a circle:
\begin{aligned}A&=\pi r^{2} \\[12pt]C&=\pi D=2\pi r\end{aligned}
Expanding upon this, at National 5 level you are also expected to know how to calculate the length of an arc and the area of a sector.
Length of an Arc
Remember that an arc is just a small section of a circle’s circumference. At the ends of any arc, radii can be drawn to create a sector:
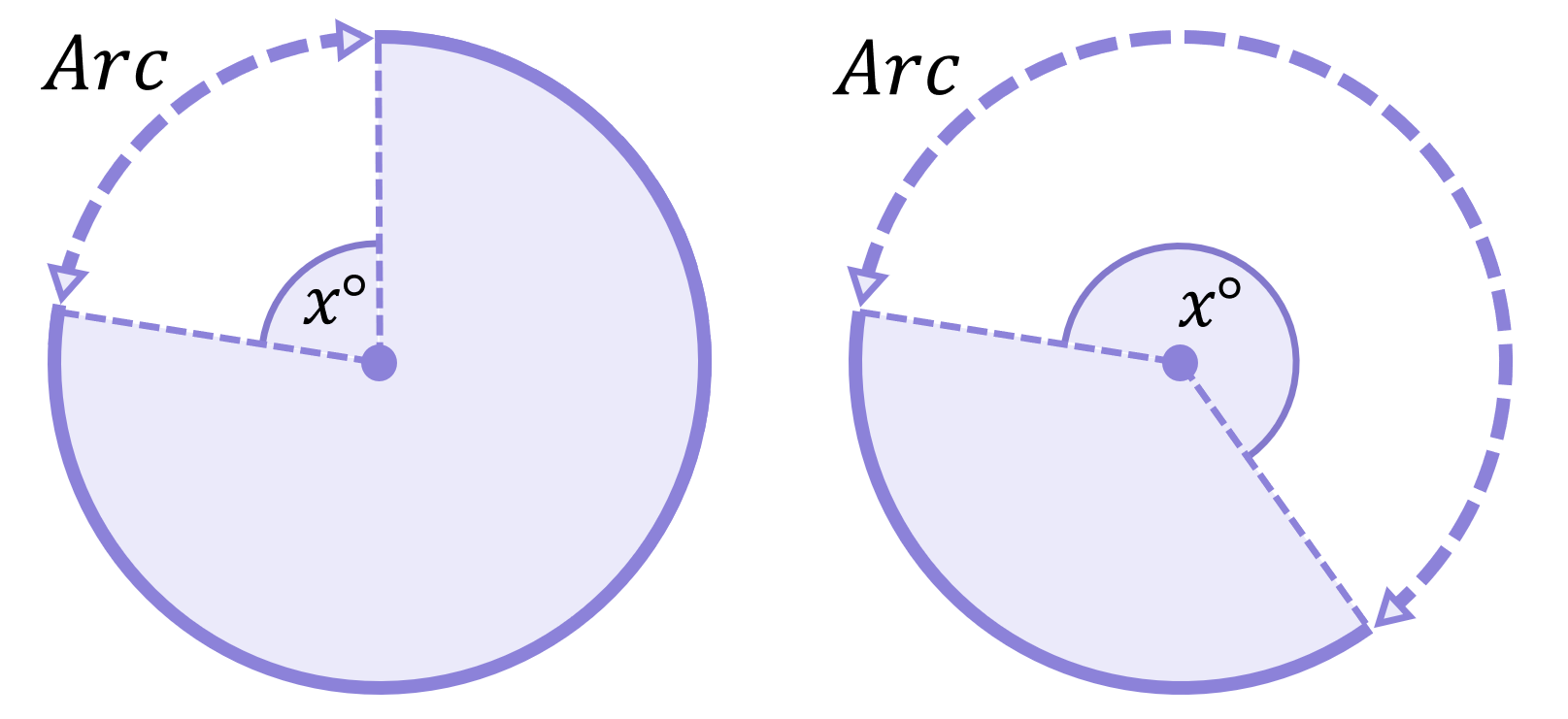
Can you see the angles highlighted in the diagrams above? We say these angles are “subtended” by the arcs.
The length of an arc is determined by the angle subtended by the arc (\boldsymbol{x^\circ}):
\begin{aligned}\textbf{Arc length}=\boldsymbol{\frac{x}{360}\times\pi D}\end{aligned}
In simple terms, this formula works out the “small section” or fraction (\frac{x}{360}) of the overall circumference (\pi D) that the arc length represents. The overall circle, like all circles, has an angle of 360^\circ, so the angle subtended by the arc must be less than this. This fraction (\frac{x}{360}) is then multiplied by the \pi D term which we know is just the circumference of the circle (since C=\pi D), resulting in an answer which is a fraction of the circumference. This should make sense since we defined an arc to be just a small section of the circumference!
Using this formula should not be too challenging, as the following examples show:
Example 1
Calculate the length of the arc shown:
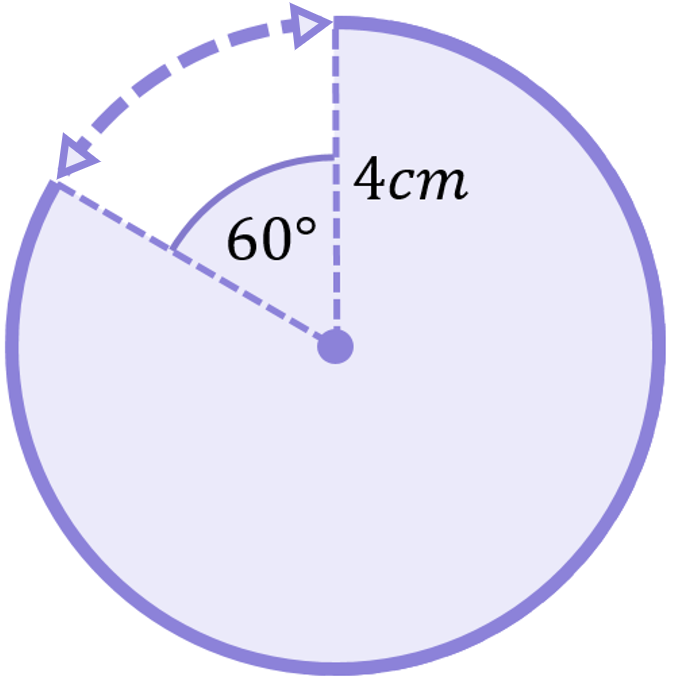
We are given the radius (r=4), from which we can easily calculate the diameter:
\begin{aligned}D&=2r \\[12pt]D&=2(4) \\[12pt]D&=8cm\end{aligned}
Since we are given the angle subtended by the arc, we can employ the new formula we just learned to calculate the length of an arc:
\begin{aligned}\text{Arc length}&=\frac{x}{360}\times\pi D \\[12pt]\text{Arc length}&=\frac{60}{360}\times\pi (8) \\[12pt]\text{Arc length}&=4.2cm\end{aligned}
Example 2
Determine the length of the circle’s diameter:
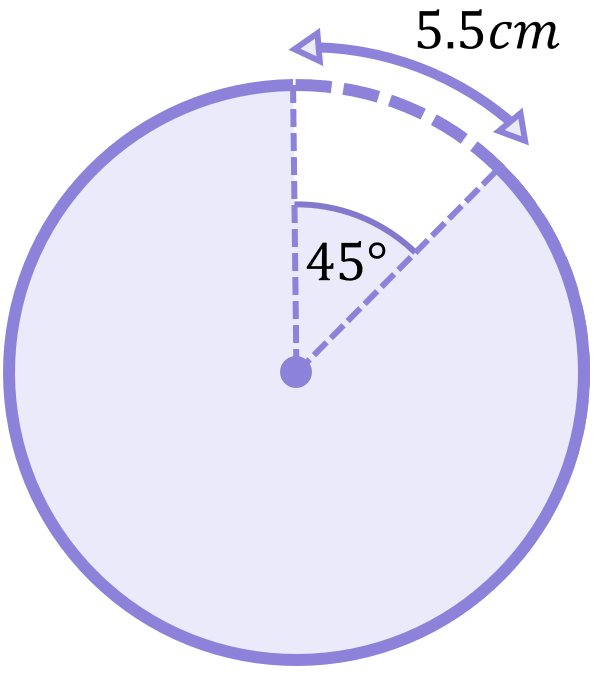
This will require using our new formula in a rearranged form. We must rearrange to make the diameter the subject of the equation:
\begin{aligned}\text{Arc length}&=\frac{x}{360}\times\pi D \\[12pt]360\times\text{Arc length}&=x\times\pi D \\[12pt]\frac{360\times\text{Arc length}}{x}&=\pi D \\[12pt]\frac{360\times\text{Arc length}}{x\pi}&=D \\[12pt]D&=\frac{360\times (5.5)}{(45)\pi} \\[12pt]D&=14cm\end{aligned}
Area of a Sector
Remember that a sector is the “pizza slice” created when an angle is subtended by an arc:
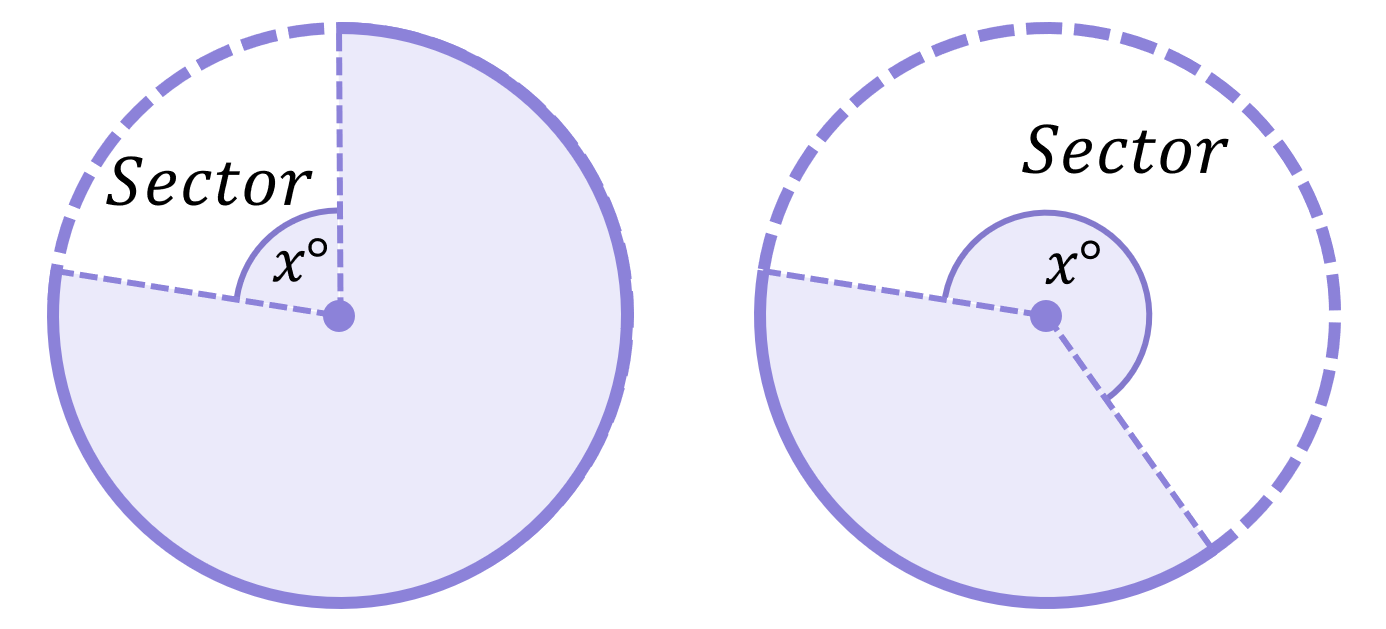
Just like the length of an arc, the area of a sector is also determined by the angle subtended by the arc (\boldsymbol{x^\circ}):
\begin{aligned}\textbf{Sector area}=\boldsymbol{\frac{x}{360}\times\pi r^{2}}\end{aligned}
This formula works in essentially the same way as the previous formula for the length of an arc. In simple terms, this formula works out the “small section” or fraction (\frac{x}{360}) of the overall area (\pi r^{2}) of the circle that the sector represents. The overall circle has an angle of 360^\circ, so the angle subtended by the arc must be less than this. This fraction (\frac{x}{360}) is then multiplied by the \pi r^{2} term which we know is just the area of the full circle (since A=\pi r^{2}), resulting in an answer which is a fraction of the area. This should make sense since we defined a sector to be just a small section of the overall circle’s area!
As with the arc length formula, using the area of a sector formula should not be too challenging, as the following examples show:
Example 3
Calculate the area of the sector shown:
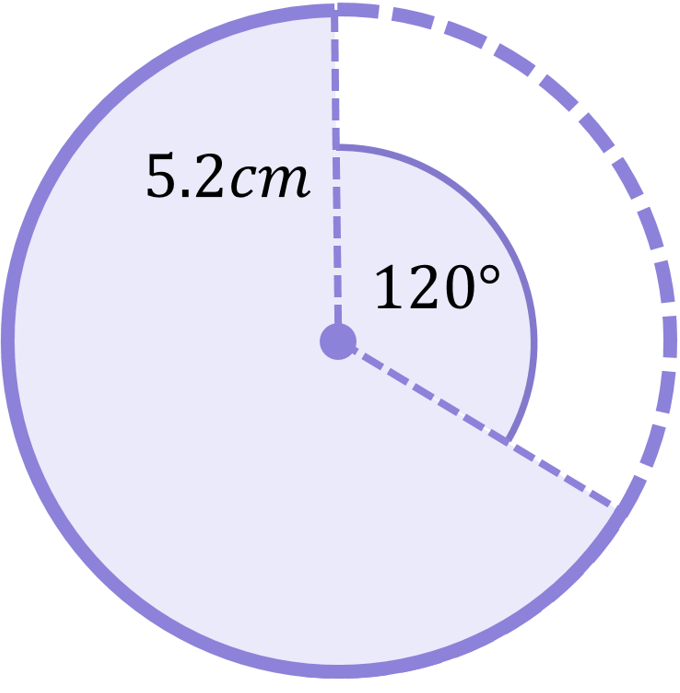
We have all we need to jump right into the sector area calculation:
\begin{aligned}\text{Sector area}&=\frac{x}{360}\times\pi r^{2} \\[12pt]\text{Sector area}&=\frac{120}{360}\times\pi (5.2)^{2} \\[12pt]\text{Sector area}&=28.3cm^{2}\end{aligned}
Example 4
A sector of a circle has an area of 30cm^{2} and an angle of 72^\circ. Calculate the radius of the circle.
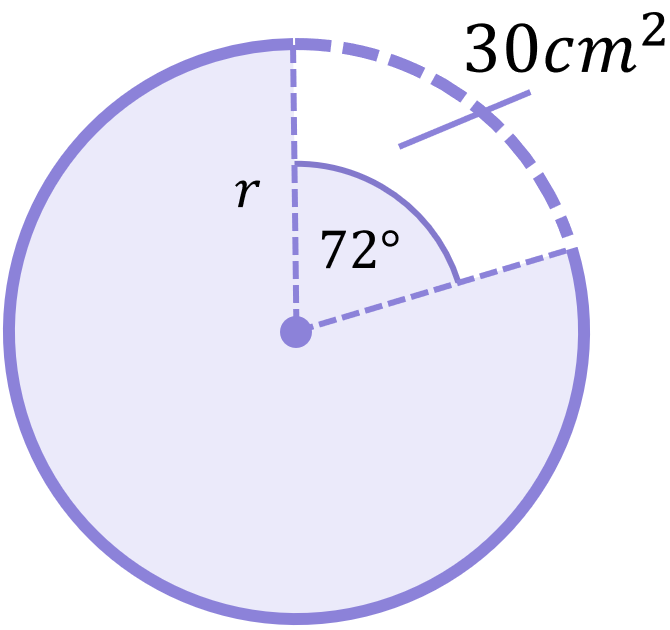
Once again we must rearrange our new formula to make the term we want to calculate (the radius) the subject:
\begin{aligned}\text{Sector area}&=\frac{x}{360}\times\pi r^{2} \\[12pt]360\times\text{Sector area}&=x\times\pi r^{2} \\[12pt]\frac{360\times\text{Sector area}}{x}&=\pi r^{2} \\[12pt]\frac{360\times\text{Sector area}}{x\pi}&=r^{2}\end{aligned}
Substituting what we know into the equation:
\begin{aligned}r^{2}&=\frac{360\times (30)}{(72)\pi} \\[12pt]r^{2}&=47.75 \\[12pt]r&=\sqrt{47.75} \\[12pt]r&=6.9cm\end{aligned}
Key Outcomes
Both the length of an arc and the area of a sector are determined by the angle subtended by the arc (x^\circ):
\begin{aligned}\text{Arc length}&=\frac{x}{360}\times\pi D \\[18pt]\text{Sector area}&=\frac{x}{360}\times\pi r^{2} \\[18pt]\end{aligned}