Area of a Circle
Area is the amount of space inside the boundary of a flat (i.e. 2-dimensional) object.
By this stage you will be familiar with calculating the areas of most standard shapes, including circles. The key area formulas you should know are given below as a reminder:




Calculating the area of a circle is too basic a problem to be asked directly at the National 5 level. At this level, you’re much more likely to be aksed to calculate the area of a sector:
Area of a Sector
Remember that a sector is the “pizza slice” created when an angle is subtended by an arc:
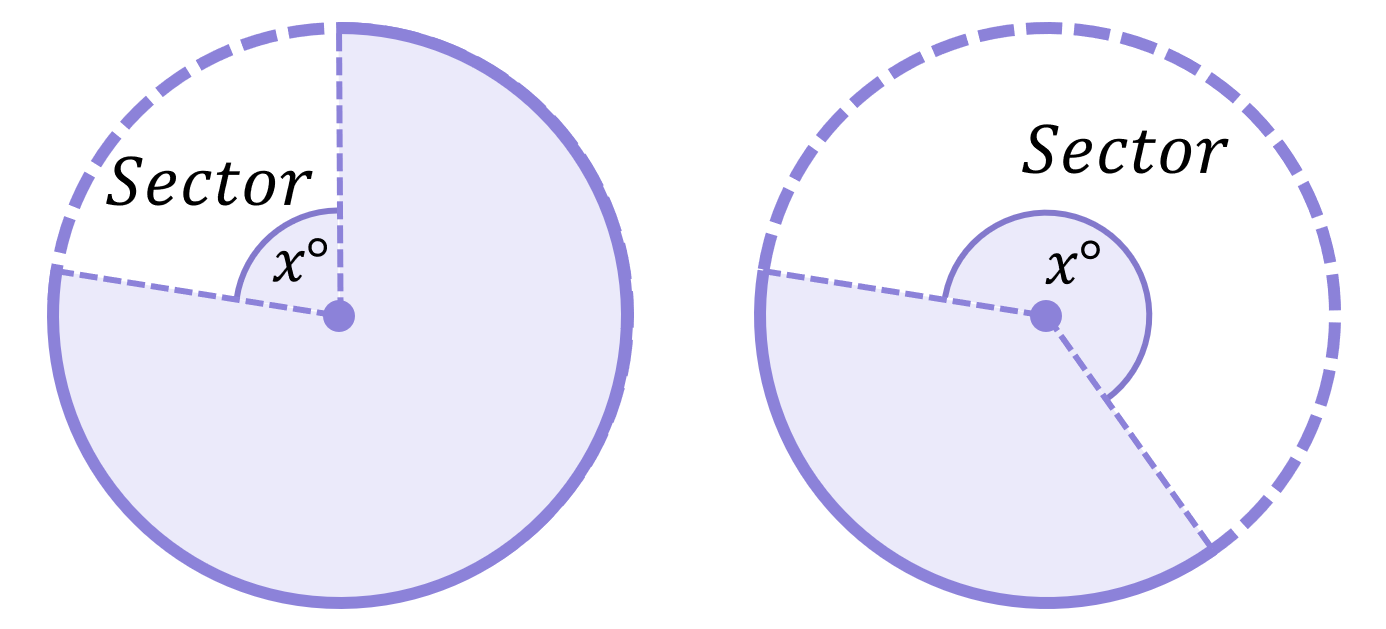
The area of a sector is determined by the angle subtended by the arc (\boldsymbol{x^\circ}):
\begin{aligned}\textbf{Sector area}=\boldsymbol{\frac{x}{360}\times\pi r^{2}}\end{aligned}
In simple terms, this formula works out the “small section” or fraction (\frac{x}{360}) of the overall area (\pi r^{2}) of the circle that the sector represents. The overall circle has an angle of 360^\circ, so the angle subtended by the arc must be less than this. This fraction (\frac{x}{360}) is then multiplied by the \pi r^{2} term which we know is just the area of the full circle (since A=\pi r^{2}), resulting in an answer which is a fraction of the area. This should make sense since a sector is just a small section of the overall circle’s area!
Using the area of a sector formula should not be too challenging, as the following examples show:
Example 1
Calculate the area of the sector shown:
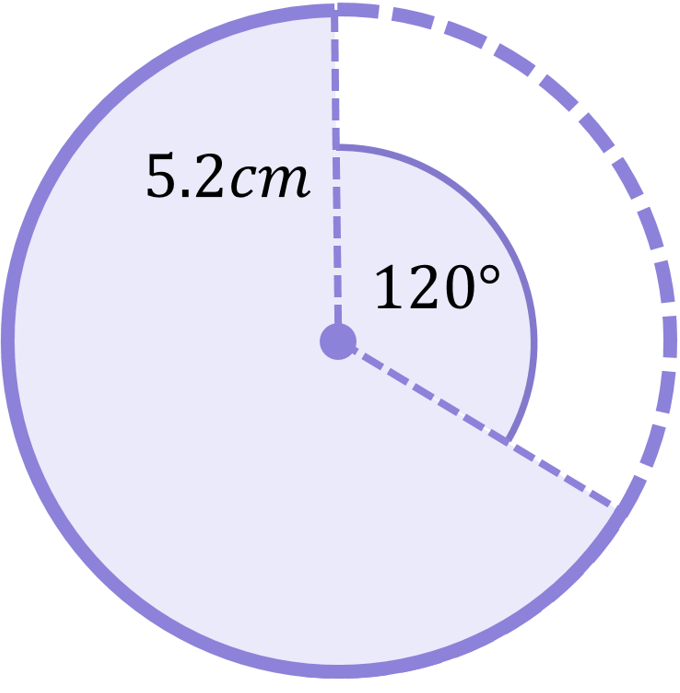
We have all we need to jump right into the sector area calculation:
\begin{aligned}\text{Sector area}&=\frac{x}{360}\times\pi r^{2} \\[12pt]\text{Sector area}&=\frac{120}{360}\times\pi (5.2)^{2} \\[12pt]\text{Sector area}&=28.3cm^{2}\end{aligned}
Example 2
A sector of a circle has an area of 30cm^{2} and an angle of 72^\circ. Calculate the radius of the circle.
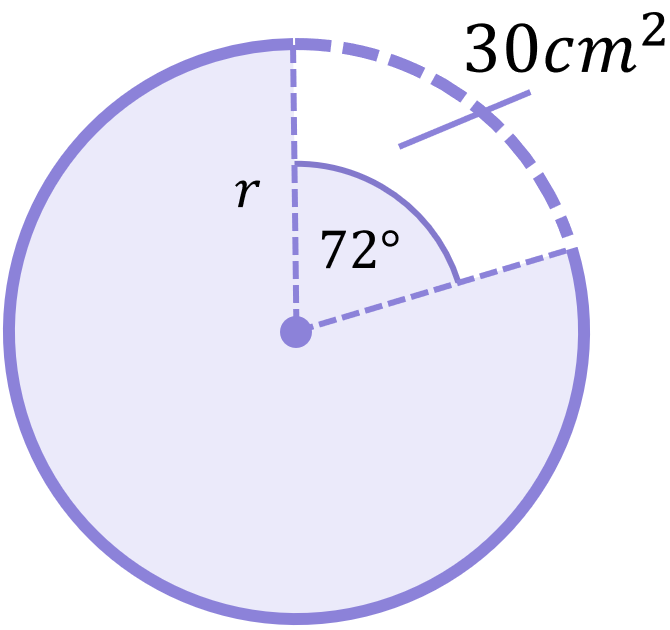
Once again we must rearrange our new formula to make the term we want to calculate (the radius) the subject:
\begin{aligned}\text{Sector area}&=\frac{x}{360}\times\pi r^{2} \\[12pt]360\times\text{Sector area}&=x\times\pi r^{2} \\[12pt]\frac{360\times\text{Sector area}}{x}&=\pi r^{2} \\[12pt]\frac{360\times\text{Sector area}}{x\pi}&=r^{2}\end{aligned}
Substituting what we know into the equation:
\begin{aligned}r^{2}&=\frac{360\times (30)}{(72)\pi} \\[12pt]r^{2}&=47.75 \\[12pt]r&=\sqrt{47.75} \\[12pt]r&=6.9cm\end{aligned}
Key Outcomes
The area of a circle is given by the equation:
\begin{aligned}\text{Area}&=\pi r^{2}\end{aligned}
The area of a sector is determined by the angle subtended by the arc (x^\circ):
\begin{aligned}\text{Sector area}&=\frac{x}{360}\times\pi r^{2} \\[18pt]\end{aligned}