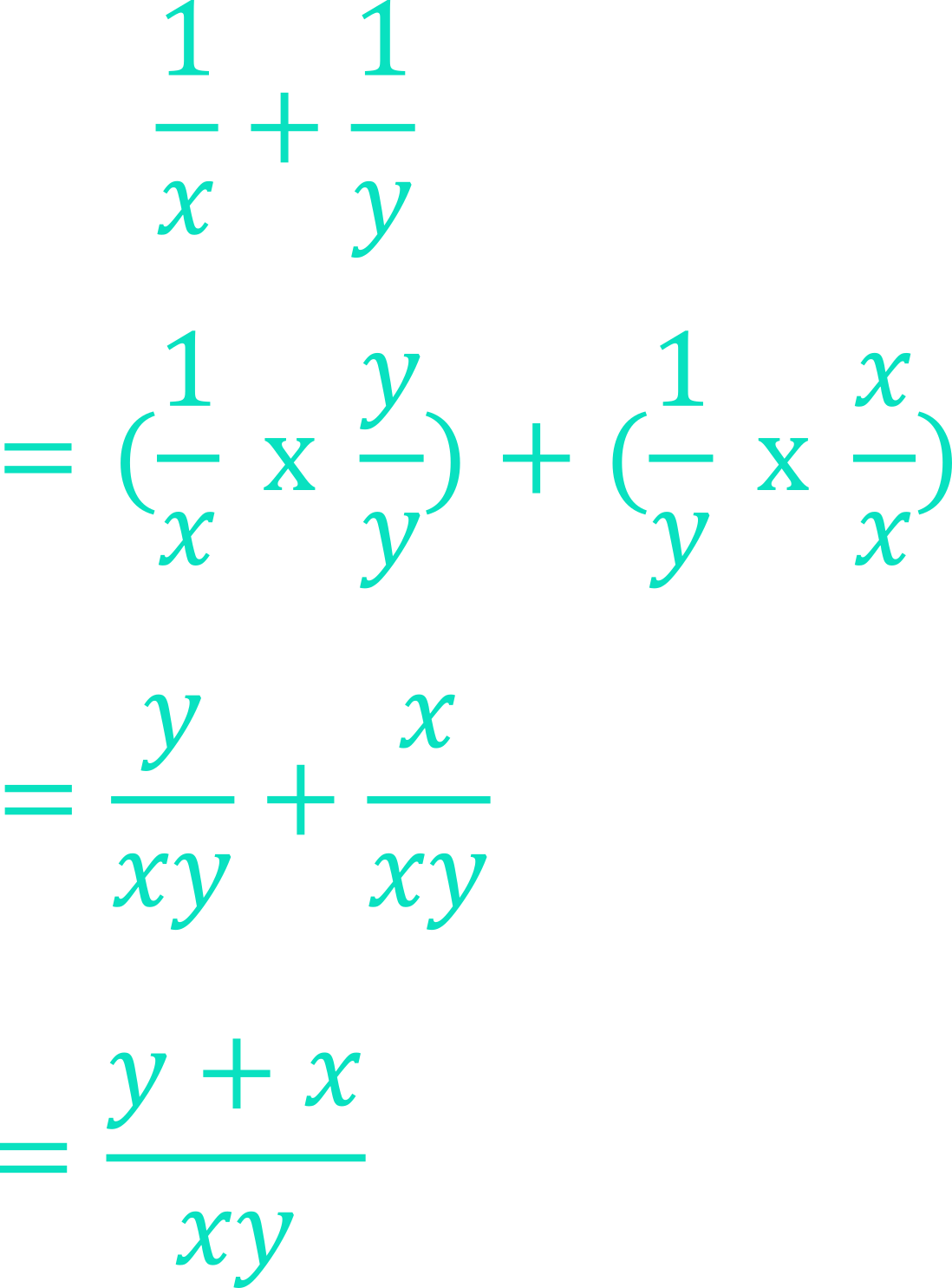Algebraic fractions are simply fractions where the numerator and/or the denominator contains an algebraic term instead of simple numbers. However, the methods for multiplying, dividing, adding or subtracting normal fractions apply to algebraic fractions in exactly the same way.

To multiply fractions, multiply the numerators together to get the new numerator and multiply the denominators together to get the new denominator. Or, “multiply the tops and multiply the bottoms” for short:

\begin{aligned}&\textcolor{white}{=}\frac{2}{3}\times\frac{y+1}{4}\ \\[12pt]&=\frac{2\times(y+1)}{3\times4}\ \\[12pt]&=\frac{2y+2}{12} \\[12pt]&=\frac{\sout2\times(y+1)}{\sout2\times6} \\[12pt]&=\frac{y+1}{6}\end{aligned}

\begin{aligned}&\textcolor{white}{=}\frac{2y}{5}\times\frac{8}{4y} \\[12pt]&=\frac{2y\times8}{5\times4y} \\[12pt]&=\frac{16y}{20y}=\frac{16}{20}=\frac{\sout4\times4}{\sout4\times5}=\frac{4}{5}\end{aligned}

To divide fractions, flip the top and bottom numbers of the divisor around (note, the divisor is the second fraction), change the division sign to a multiplication sign, and multiply the two fractions normally. Or, “flip the second fraction and multiply” for short:

\begin{aligned}&\textcolor{white}{=}\frac{4}{9}\div\frac{1}{3y} \\[12pt]&=\frac{4}{9}\times\frac{3y}{1} \\[12pt]&=\frac{12y}{9}=\frac{\sout3\times4y}{\sout3\times3}=\frac{4y}{3}\end{aligned}

\begin{aligned}&\textcolor{white}{=}\frac{3}{2y}\div\frac{8y}{6y^2} \\[12pt]&=\frac{3}{2y}\times\frac{6y^2}{8y} \\[12pt]&=\frac{18y^2}{16y^2}=\frac{18}{16}=\frac{\sout2\times9}{\sout2\times8}=\frac{9}{8}\end{aligned}

As was the case with normal fractions, adding or subtracting algebraic fractions is more difficult because the denominators have to be the same, and if they are not the same, then we need to make adjustments.

You face the same three possibilities when adding or subtracting algebraic fractions that you do with standard fractions:

1) The fractions have the same denominators
2) The fractions have different denominators, but one is a factor of the other
3) The fractions have different denominators, and neither is a factor of the other

As with basic fractions, this scenario is also very straightforward with algebraic fractions. As the fractions have the same denominators, they are both the same type of fraction (i.e. they are like-terms), so they add without any trouble:

\begin{aligned}&\textcolor{white}{=}\frac{2}{x}+\frac{4}{x} \\[12pt]&=\frac{2+4}{x}=\frac{6}{x}\end{aligned}

\begin{aligned}&\textcolor{white}{=}\frac{3}{3y}+\frac{6x}{3y} \\[12pt]&=\frac{3+6x}{3y} \\[12pt]&=\frac{\sout3\times(1+2x)}{\sout3\times y}=\frac{1+2x}{y}\end{aligned}

As with basic fractions, the fractions having different denominators means they are not like-terms, so we cannot add them in their current form. We have to make adjustments to one of the fractions to make the denominators the same (i.e. make them like-terms) before we can add them.

Let’s take a simple example:

\begin{aligned}\frac{1}{y}+\frac{1}{2y}\end{aligned}

One of the fractions has a denominator of y and the other has a denominator of 2y. Although we do not know the numerical value of y, this does not matter as it is obvious that y cannot possibly be the same as 2y (excluding the case where y=0). For example, if y=5, then 2y=10, so y and 2y must represent different values, and the fractions therefore have different denominators.

Notice however, that y is a factor of 2y (since y\times2=2y, y fits into 2y perfectly), thus we can make an adjustment as follows:

\begin{aligned}&\textcolor{white}{=}\frac{1}{y}+\frac{1}{2y} \\[12pt]&=\left(\frac{1}{y}\times\frac{2}{2}\right)+\frac{1}{2y} \\[12pt]&=\frac{2}{2y}+\frac{1}{2y} \\[12pt]&=\frac{3}{2y}\end{aligned}

This is exactly the same method you have no doubt used when dealing with normal fractions with different denominators. Where one of the denominators is a factor of the other, we need only adjust one of the fractions. More complex problems require adjusting both fractions, but we will see that in the next section of this topic.

Follow these other examples and you will begin to see that the process is very similar each time:

\begin{aligned}&\textcolor{white}{=}\frac{3}{z}+\frac{2}{z^2} \\[12pt]&=\left(\frac{3}{z}\times\frac{z}{z}\right)+\frac{2}{z^2} \\[12pt]&=\frac{3z}{z^2}+\frac{2}{z^2} \\[12pt]&=\frac{3z+2}{z^2}\end{aligned}

\begin{aligned}&\textcolor{white}{=}5+\frac{5x+5}{y} \\[12pt]&=\frac{5}{1}+\frac{5x+5}{y} \\[12pt]&=\left(\frac{5}{1}\times\frac{y}{y}\right)+\frac{5x+5}{y} \\[12pt]&=\frac{5y}{y}+\frac{5x+5}{y} \\[12pt]&=\frac{5y+5x+5}{y} \\[12pt]&=\frac{5(y+x+1)}{y}\end{aligned}

Just as with normal fractions, as the denominators are different in this scenario, and since neither denominator is a factor of the other, adjusting one fraction will not be enough, so we must adjust both.

An example of this would be:

\begin{aligned}\frac{1}{x}+\frac{1}{y}\end{aligned}

As with normal fractions, when the denominators are different we must convert the fractions. Since x and y are algebraic terms, we do not know their numerical values. Since x doesn’t fit into y, and y doesn’t fit into x, we have to change the denominators of both fractions into the lowest common denominator.

But how can we determine the lowest common denominator if we do not know the numerical values of x and y? How can we determine any term that x and y both fit into perfectly for that matter?

In our example:

\begin{aligned}\frac{1}{x}+\frac{1}{y}\end{aligned}

The lowest common denominator is therefore:

\begin{aligned}x\times y=xy\end{aligned}

We can understand why this is the case by comparing it to some easier numerical examples. Imagine instead we were trying to add the following fractions:

\begin{aligned}\frac{1}{2}+\frac{1}{5}\end{aligned}

We would establish the lowest common denominator as normal. The lowest common multiple of 2 and 5 is 10 (i.e. 10 is the lowest number that both 2 and 5 fit into perfectly), so both fractions should have 10 as their denominator.

Notice that 10, the lowest common denominator, is also the product of the two denominators, i.e. 2\times 5=10.

Since 10 is obtained by taking the product of 2 and 5, we can be sure that both 2 and 5 fit into 10 an exact number of times. Since 10=2\times 5, we could either say that:

2 fits into 10 five times
or
5 fits into 10 two times

Whichever way you look at it, it is clear that both 2 and 5 fit into 10 an exact number of times and that 10 is therefore a common multiple of 2 and 5.

To stress the point with a further numerical example:

\begin{aligned}\frac{2}{3}+\frac{4}{7}\end{aligned}

As this is a numerical example it is easy to determine that the lowest common multiple of 3 and 7 is 21, so both fractions should have 21 as their denominator.

However, notice that 21, the lowest common denominator, can also be obtained by taking the product of the two denominators, i.e. 3\times 7=21, and therefore we could either say that:

3 fits into 21 seven times
or
7 fits into 21 three times

Returning to our algebraic example:

\begin{aligned}\frac{1}{x}+\frac{1}{y}\end{aligned}

If we knew the numerical values of x and y, it would be simple to calculate their lowest common multiple. Since we do not know their numerical values, the only term we can be sure that both x and y fit into an exact number of times is their product:

\begin{aligned}x\times y=xy\end{aligned}

Since xy, the lowest common denominator, is obtained by taking the product of the two denominators, i.e. x\times y = xy, then, just as with our numerical examples, we could either say that:

x fits into xy ‘y’ times
or
y fits into xy ‘x’ times

Having now firmly established that xy is the lowest common denominator, we are ready to adjust both fractions such that they have xy as their denominator, and then actually add the fractions:

\begin{aligned}&\textcolor{white}{=}\frac{1}{x}+\frac{1}{y} \\[12pt]&=\left(\frac{1}{x}\times\frac{y}{y}\right)+\left(\frac{1}{y}\times\frac{x}{x}\right) \\[12pt]&=\frac{y}{xy}+\frac{x}{xy} \\[12pt]&=\frac{y+x}{xy}\end{aligned}

Try the following examples to get comfortable with the methodology:

\begin{aligned}&\textcolor{white}{=}\frac{3x}{4}-\frac{2}{5x} \\[12pt]&=\left(\frac{3x}{4}\times\frac{5x}{5x}\right)-\left(\frac{2}{5x}\times\frac{4}{4}\right) \\[12pt]&=\frac{15x^2}{20x}\ -\ \frac{8}{20x} \\[12pt]&=\frac{15x^2-8}{20x}\end{aligned}

\begin{aligned}&\textcolor{white}{=}\frac{(x-2)}{5}+\frac{(x+3)}{2} \\[12pt]&=\Bigg(\frac{\left(x-2\right)}{5}\times\frac{2}{2}\Bigg)+\Bigg(\frac{\left(x+3\right)}{2}\times\frac{5}{5}\Bigg) \\[12pt]&=\frac{2\left(x-2\right)}{10}+\frac{5\left(x+3\right)}{10} \\[12pt]&=\frac{2x-4}{10}+\frac{5x+15}{10} \\[12pt]&=\frac{2x-4+5x+15}{10} \\[12pt]&=\frac{7x+11}{10}\end{aligned}

\begin{aligned}&\textcolor{white}{=}\frac{3}{(x+4)}+\frac{4}{(x-1)} \\[12pt]&=\Bigg(\frac{3}{\left(x+4\right)}\times\frac{\left(x-1\right)}{\left(x-1\right)}\Bigg)+\Bigg(\frac{4}{\left(x-1\right)}\times\frac{\left(x+4\right)}{\left(x+4\right)}\Bigg) \\[12pt]&=\frac{3\left(x-1\right)}{\left(x+4\right)(x-1)}+\frac{4(x+4)}{\left(x-1\right)(x+4)}\ \\[12pt]&=\frac{3x-3}{\left(x+4\right)(x-1)}+\frac{4x+16}{\left(x-1\right)(x+4)} \\[12pt]&=\frac{3x-3+4x+16}{\left(x+4\right)(x-1)} \\[12pt]&=\frac{7x+13}{\left(x+4\right)(x-1)}\end{aligned}